[数据结构与算法]团队程序设计天梯赛-3.19排位赛总结

7-1 冠军魔术 (10 分)

题目

2018年FISM（世界魔术大会）近景总冠军简纶廷的表演中有一个情节：以桌面上一根带子为界，当他将纸牌从带子的一边推到另一边时，纸牌会变成硬币；把硬币推回另一边会变成纸牌。

这里我们假设纸牌会变成等量的硬币，而硬币变成纸牌时，纸牌的数量会加倍。那么给定纸牌的初始数量，当他来回推了 N 次（来/回各算一次）后，手里拿的是纸牌还是硬币？数量是多少？

输入格式：
输入在一行里给出两个正整数，分别是纸牌的初始数量和魔术师推送的次数。这里假设初始状态下魔术师手里全是纸牌。

输出格式：
如果最后魔术师手里是纸牌，输出 0 和纸牌数量；如果是硬币，则输出 1 和硬币数量。数字间须有 1 个空格。题目保证结果数值不超出整型范围（即 2
31
?1）。

输入样例 1：

3 7

输出样例 1：

1 24

输入样例 2：

8 4

输出样例 2：

0 32

知识点

找规律

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	int num, n;
	cin >> num >> n;
	if(n%2==0) cout << "0 " << ?num*(int)pow(2, n/2);
	else cout << "1 " << ?num*(int)pow(2, (n-1)/2);
	return 0;
}

7-2 单词长度 (10 分)

题目

你的程序要读入一行文本，其中以空格分隔为若干个单词，以.结束。你要输出每个单词的长度。这里的单词与语言无关，可以包括各种符号，比如it’s算一个单词，长度为4。注意，行中可能出现连续的空格；最后的.不计算在内。

输入格式:
输入在一行中给出一行文本，以.结束

输出格式:
在一行中输出这行文本对应的单词的长度，每个长度之间以空格隔开，行末没有最后的空格。

输入样例:

It's great to see you here.

输出样例:

4 5 2 3 3 4

注意点

注意会出现一个或多个空格后面接句号的特殊情况
注意若长度为0，不输出0。比如：23 . , 输出：2

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	string s;
	int flag = 0;
	while(cin>>s) {
		if(s==".") break;
		if(flag) cout << " ";
		flag = 1;
		if(s.back()!='.') cout << s.length();
		else if(s.length()>1) cout << s.length()-1;
	}
	return 0;
}

7-3 组个最小数 (15 分)

题目

给定数字0-9各若干个。你可以以任意顺序排列这些数字，但必须全部使用。目标是使得最后得到的数尽可能小（注意0不能做首位）。例如：给定两个0，两个1，三个5，一个8，我们得到的最小的数就是10015558。

现给定数字，请编写程序输出能够组成的最小的数。

输入格式：
输入在一行中给出10个非负整数，顺序表示我们拥有数字0、数字1、……数字9的个数。整数间用一个空格分隔。10个数字的总个数不超过50，且至少拥有1个非0的数字。

输出格式：
在一行中输出能够组成的最小的数。

输入样例：

2 2 0 0 0 3 0 0 1 0

输出样例：

10015558

知识点

find_first_of()和find_last_of的使用：函数find_first_of() 查找在字符串中第1个出现的字符c，而函数find_last_of()查找最后一个出现的c。匹配的位置是返回值。如果没有匹配发生，则函数返回-1.
find_first_of()和 find_last_of()

代码

参考代码(按顺序输入后交换）：

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main() {
	string s = "";
	int n;
	for(char i='0'; i<='9'; i++) {
		cin >> n;
		for(int j=0; j<n; j++) s += i;
	}
	int pos = s.find_last_of('0');
	if(pos!=-1) swap(s[0], s[pos+1]);
	cout << s;
	return 0;
}

我的代码（排序后如果第一个为0则交换）：

#include <bits/stdc++.h>
using namespace std;
int main(){
	int a[10];
	vector<int> v;
	for(int i=0;i<10;i++){
		cin>>a[i];
	}
	for(int i=0;i<10;i++){
		while(a[i]--){
			v.push_back(i);
		}
	}
	sort(v.begin(),v.end());
	int pos;
	for(int i=0;i<v.size();i++){
		if(v[i]!=0){
			pos = i;
			break;
		}
	}
	if(v[0] == 0){
		int t = v[0];
		v[0] = v[pos];
		v[pos] = t;
	}
	for(int i=0;i<v.size();i++){
		cout<<v[i];
	}
}

7-4 检查密码 (15 分)

题目

本题要求你帮助某网站的用户注册模块写一个密码合法性检查的小功能。该网站要求用户设置的密码必须由不少于6个字符组成，并且只能有英文字母、数字和小数点 .，还必须既有字母也有数字。

输入格式：
输入第一行给出一个正整数 N（≤ 100），随后 N 行，每行给出一个用户设置的密码，为不超过 80 个字符的非空字符串，以回车结束。

注意： 题目保证不存在只有小数点的输入。

输出格式：
对每个用户的密码，在一行中输出系统反馈信息，分以下5种：

如果密码合法，输出Your password is wan mei.；
如果密码太短，不论合法与否，都输出Your password is tai duan le.；
如果密码长度合法，但存在不合法字符，则输出Your password is tai luan le.；
如果密码长度合法，但只有字母没有数字，则输出Your password needs shu zi.；
如果密码长度合法，但只有数字没有字母，则输出Your password needs zi mu.。
输入样例：

5
123s
zheshi.wodepw
1234.5678
WanMei23333
pass*word.6

输出样例：

Your password is tai duan le.
Your password needs shu zi.
Your password needs zi mu.
Your password is wan mei.
Your password is tai luan le.

思路

使用getline（）进行字符串的输入
分别对不同情况进行处理即可

知识点

isalpha():判断是否为字母
isdigit():判断是否为数字（注意digit的拼写！！！）

代码

#include<iostream>
#include<string>
using namespace std;
int main() {
	int n;
	cin >> n;
	getchar();
	string s;
	int flag, letter, num;
	for(int i=0; i<n; i++) {
		flag = 1;
		letter = num = 0;
		getline(cin, s);//含有空格的string字符串的读入
		if(s.size()<6) {
			cout << "Your password is tai duan le.\n";
			continue;
		}
		for(int k=0; s[k]!='\0'; k++) {
			if(isalpha(s[k])) letter = 1;//含有字母
			else if(isdigit(s[k])) num = 1;//含有数字
			else if(s[k]!='.') { //只要碰到非法字符就退出
				flag = 0;
				break;
			}
		}
		if(flag==0) cout << "Your password is tai luan le.\n";
		else if(letter==0) cout << "Your password needs zi mu.\n";
		else if(num==0) cout << "Your password needs shu zi.\n";
		else cout << "Your password is wan mei.\n";
	}
}

7-5 大炮打蚊子 (20 分)

题目

现在，我们用大炮来打蚊子：蚊子分布在一个M×N格的二维平面上，每只蚊子占据一格。向该平面的任意位置发射炮弹，炮弹的杀伤范围如下示意：

O
OXO
 O

其中，X为炮弹落点中心，O为紧靠中心的四个有杀伤力的格子范围。若蚊子被炮弹命中（位于X格），一击毙命，若仅被杀伤（位于O格），则损失一半的生命力。也就是说，一次命中或者两次杀伤均可消灭蚊子。现在给出蚊子的分布情况以及连续k发炮弹的落点，给出每炮消灭的蚊子数。

输入格式:
第一行为两个不超过20的正整数M和N，中间空一格，表示二维平面有M行、N列。

接下来M行，每行有N个0或者#字符，其中#表示所在格子有蚊子。

接下来一行，包含一个不超过400的正整数k，表示发射炮弹的数量。

最后k行，每行包括一发炮弹的整数坐标x和y（0≤x<M，0≤y<N），之间用一个空格间隔。

输出格式:
对应输入的k发炮弹，输出共有k行，第i行即第i发炮弹消灭的蚊子数。

输入样例:

5 6
00#00#
000###
00#000
000000
00#000
2
1 2
1 4

输出样例:

0
2

思路

将有蚊子的地方设为2，大炮刚好命中则-2，其周边区域则-1，每次统计数量

代码

#include<bits/stdc++.h>
using namespace std;
int a[21][21];
int fun(int x, int y)
{
	//处理a[x][y]的蚊子
	int res = 0;
	if(a[x][y]==1) res = 1, a[x][y] = 0;
	else if(a[x][y]==2) a[x][y] = 1;
	return res;
}
int main() {
	int m, n;
	cin >> m >> n;
	char c;
	for(int i=0; i<m; i++)
		for(int j=0; j<n; j++) {
			cin >> c;
			if(c=='#') a[i][j] = 2;
		}
	int k;
	cin >> k;
	while(k--) {
		int x, y;
		cin >> x >> y;
		int res = 0;
		if(a[x][y]>0) res++, a[x][y] = 0;
		if(x>0) res += fun(x-1, y);
		if(x<m-1) res += fun(x+1, y);
		if(y>0) res += fun(x, y-1);
		if(y<n-1) res += fun(x, y+1);
		cout << res << endl;
	}
	return 0;
}

7-6 出栈序列的合法性 (20 分)

题目描述

给定一个最大容量为 M 的堆栈，将 N 个数字按 1, 2, 3, …, N 的顺序入栈，允许按任何顺序出栈，则哪些数字序列是不可能得到的？例如给定 M=5、N=7，则我们有可能得到{ 1, 2, 3, 4, 5, 6, 7 }，但不可能得到{ 3, 2, 1, 7, 5, 6, 4 }。

输入格式：
输入第一行给出 3 个不超过 1000 的正整数：M（堆栈最大容量）、N（入栈元素个数）、K（待检查的出栈序列个数）。最后 K 行，每行给出 N 个数字的出栈序列。所有同行数字以空格间隔。

输出格式：
对每一行出栈序列，如果其的确是有可能得到的合法序列，就在一行中输出YES，否则输出NO。

输入样例：

5 7 5
1 2 3 4 5 6 7
3 2 1 7 5 6 4
7 6 5 4 3 2 1
5 6 4 3 7 2 1
1 7 6 5 4 3 2

输出样例：

YES
NO
NO
YES
NO

思路

数组a存放待比较的出栈序列，pos表示数组a当前要出栈的数的下标
st是容量为m的栈， 初始时1入栈。num顺序取自1~n，初值为1
关键思想就是不断出栈和不断入栈，当既不能出栈也不能入栈，退出循环
循环后根据是否栈空判断YES/NO

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	int m, n, k;
	cin >> m >> n >> k;
	int a[1001];
	while(k--) {
		for(int i=1; i<=n; i++) cin >> a[i];
		stack<int> st;
		st.push(1);
		int num = 2, pos = 1;
		int flag = 1;
		while(flag) {
			flag = 0;
			while(!st.empty() && pos<=n && st.top()==a[pos]) {
				//满足条件时不断出栈
				st.pop();
				pos++;
				flag = 1;
			}
			while(st.size()<m && num<=n && num<=a[pos]) {
				//满足条件时不断入栈
				st.push(num);
				num++;
				flag = 1;
			}
		}
		if(st.empty()) cout << "YES\n";
		else cout << "NO\n";
	}
	return 0;
}

7-7 社交网络图中结点的“重要性”计算 (25 分)

题目描述

在社交网络中，个人或单位（结点）之间通过某些关系（边）联系起来。他们受到这些关系的影响，这种影响可以理解为网络中相互连接的结点之间蔓延的一种相互作用，可以增强也可以减弱。而结点根据其所处的位置不同，其在网络中体现的重要性也不尽相同。


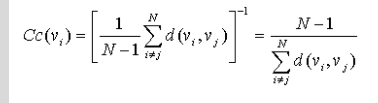
对于非连通图，所有结点的紧密度中心性都是0。

给定一个无权的无向图以及其中的一组结点，计算这组结点中每个结点的紧密度中心性。

输入格式:
输入第一行给出两个正整数N和M，其中N（≤10
4
）是图中结点个数，顺便假设结点从1到N编号；M（≤10
5
）是边的条数。随后的M行中，每行给出一条边的信息，即该边连接的两个结点编号，中间用空格分隔。最后一行给出需要计算紧密度中心性的这组结点的个数K（≤100）以及K个结点编号，用空格分隔。

输出格式:
按照Cc(i)=x.xx的格式输出K个给定结点的紧密度中心性，每个输出占一行，结果保留到小数点后2位。

输入样例:

9 14
1 2
1 3
1 4
2 3
3 4
4 5
4 6
5 6
5 7
5 8
6 7
6 8
7 8
7 9
3 3 4 9

输出样例:

Cc(3)=0.47
Cc(4)=0.62
Cc(9)=0.35

思路

使用floyd计算任两点的最短距离。
遍历需要求的点到所有点的距离并相加（若遍历图中遇到非连通（距离为原来设立的MAX值）则可以终止了）

代码

#include<bits/stdc++.h>
using namespace std;
#define MAX 100000//这个数值，只要是全大于任两点的最大距离就行。
int n, m;
int a[10001][10001];
void floyd() {
	for(int k=1; k<=n; k++)
		for(int i=1; i<=n; i++)
			for(int j=1; j<=n; j++)
				a[i][j] = min(a[i][j], a[i][k]+a[k][j]);
}
int main() {
	cin >> n >> m;
	for(int i=1; i<=n; i++)
		for(int j=1; j<=n; j++)
			a[i][j] = MAX;
	while(m--) {
		int x, y;
		cin >> x >> y;
		a[x][y] = a[y][x] = 1;
	}
	floyd();
//		for(int i=1; i<=n; i++){
//			for(int j=1; j<=n; j++){
//				cout<<a[i][j]<<" ";
//			}
//			cout<<endl;
//			
//		}
		
	int k;
	cin >> k;
	int flag = 1;
	while(k--) {
		int x;
		cin >> x;
		double dis = 0;
		for(int i=1; i<=n && flag; i++) {
			if(i==x) continue;
			if(a[x][i]==MAX) flag = 0; //一旦flag为0，以后都不用算了，结果肯定都是0
			dis += a[x][i];
		}
		if(flag==0) printf("Cc(%d)=0.00\n", x);
		else printf("Cc(%d)=%.2f\n", x, (n-1)/dis);
	}
	return 0;
}

7-8 朋友圈 (25 分)

题目描述

某学校有N个学生，形成M个俱乐部。每个俱乐部里的学生有着一定相似的兴趣爱好，形成一个朋友圈。一个学生可以同时属于若干个不同的俱乐部。根据“我的朋友的朋友也是我的朋友”这个推论可以得出，如果A和B是朋友，且B和C是朋友，则A和C也是朋友。请编写程序计算最大朋友圈中有多少人。

输入格式:
输入的第一行包含两个正整数N（≤30000）和M（≤1000），分别代表学校的学生总数和俱乐部的个数。后面的M行每行按以下格式给出1个俱乐部的信息，其中学生从1~N编号：

第i个俱乐部的人数Mi（空格）学生1（空格）学生2 … 学生Mi

输出格式:
输出给出一个整数，表示在最大朋友圈中有多少人。

输入样例:

7 4
3 1 2 3
2 1 4
3 5 6 7
1 6

输出样例:

4

思路

使用并查集不断合并有朋友关系的朋友，遍历查找各个根节点的数量的最大值即为答案
还是并查集，但这次要加速，否则最后测试点超时

代码

#include<bits/stdc++.h>
using namespace std;
int pre[30001];
int root(int x) {
//平常的找根节点方法：（会慢一点）
//	while(x!=root[x]){
//		x = root[x];
//	}
//	return x;
	return x==pre[x]? x:pre[x]=root(pre[x]);//（可以加速！！！！！）
}
void un(int x, int y) {
	int px = root(x);
	int py = root(y);
	pre[px] = py;
}
int main() {
	int n, m;
	cin >> n >> m;
	for(int i=1; i<=n; i++) pre[i] = i;
	while(m--) {
		int k, x, y;
		cin >> k;
		cin >> x;
		while(--k) {
			cin >> y;
			un(x, y);
			x = y;
		}
	}
	map<int, int> mp;
	for(int i=1; i<=n; i++)
		mp[root(i)]++;
	int max = 0;
	for(auto x:mp) if(x.second>max) max = x.second;
	cout << max;
	return 0;
}

7-9 家谱处理 (25 分)

人类学研究对于家族很感兴趣，于是研究人员搜集了一些家族的家谱进行研究。实验中，使用计算机处理家谱。为了实现这个目的，研究人员将家谱转换为文本文件。下面为家谱文本文件的实例：

John
  Robert
    Frank
    Andrew
  Nancy
    David

家谱文本文件中，每一行包含一个人的名字。第一行中的名字是这个家族最早的祖先。家谱仅包含最早祖先的后代，而他们的丈夫或妻子不出现在家谱中。每个人的子女比父母多缩进2个空格。以上述家谱文本文件为例，John这个家族最早的祖先，他有两个子女Robert和Nancy，Robert有两个子女Frank和Andrew，Nancy只有一个子女David。

在实验中，研究人员还收集了家庭文件，并提取了家谱中有关两个人关系的陈述语句。下面为家谱中关系的陈述语句实例：

John is the parent of Robert
Robert is a sibling of Nancy
David is a descendant of Robert
研究人员需要判断每个陈述语句是真还是假，请编写程序帮助研究人员判断。

输入格式:
输入首先给出2个正整数N（2≤N≤100）和M（≤100），其中N为家谱中名字的数量，M为家谱中陈述语句的数量，输入的每行不超过70个字符。

名字的字符串由不超过10个英文字母组成。在家谱中的第一行给出的名字前没有缩进空格。家谱中的其他名字至少缩进2个空格，即他们是家谱中最早祖先（第一行给出的名字）的后代，且如果家谱中一个名字前缩进k个空格，则下一行中名字至多缩进k+2个空格。

在一个家谱中同样的名字不会出现两次，且家谱中没有出现的名字不会出现在陈述语句中。每句陈述语句格式如下，其中X和Y为家谱中的不同名字：

X is a child of Y
X is the parent of Y
X is a sibling of Y
X is a descendant of Y
X is an ancestor of Y

输出格式:
对于测试用例中的每句陈述语句，在一行中输出True，如果陈述为真，或False，如果陈述为假。

输入样例:

6 5
John
  Robert
    Frank
    Andrew
  Nancy
    David
Robert is a child of John
Robert is an ancestor of Andrew
Robert is a sibling of Nancy
Nancy is the parent of Frank
John is a descendant of Andrew

输出样例:

True
True
True
False
False

思路

难点在于：1. 使用什么数据结构来存储家族关系。观察问题，使用map! mp[孩子] = 老爸 最合适。
2. 如何读入到map中，这里的难点是如何获得当前读入的名字的上一辈。这里可以使用栈。
栈里总是保存一层一层的父辈。因此栈的初值是最早祖先的父辈（设为“000”）。
再使用bk来记录上一行输入的空格数。因此bk的初值对应是最早祖先的父辈的缩进。由于最早祖先缩进
是0，因此其父辈的缩进是-2
若当前空格数k小于等于上一行的空格数bk，出栈(k+2-bk)/2次。这样栈顶一定是当前的父辈
若当前空格数k大于上一行的空格数bk，那就说明栈顶本身就是当前的父辈。
找到父辈后，mp[当前] = 栈顶。然后当前入栈，为下次做准备。同时刷新bk的值

代码

#include<bits/stdc++.h>
using namespace std;
int main() {
	int n, m;
	cin >> n >> m;
	getchar();
	stack<string> st;//用于存放一层一层的父辈序列
	st.push("000");//最早祖先的父辈设为 "000"
	int bk = -2;//上一次输入的缩进空格数，初始值为-2（最早祖先缩进为0，他的父辈就是-2）
	map<string, string> mp;//mp[孩子] = 老爸
	while(n--) {
		string s;
		getline(cin, s);
		int k;
		for(k=0; s[k] && s[k]==' '; k++);//有多少个空格
		s = s.substr(k);//不取空格
		if(k <= bk)//当前空格数小于等于上次，说明上次一定不是当前的父辈
			for(int i=k; i<=bk; i+=2) st.pop();//把不是父辈的出栈
		mp[s] = st.top();//栈顶是当前的父辈
		st.push(s);//本次输入入栈
		bk = k; //刷新上次空格数
	}
	string qs[100];
	while(m--) {
		int res = 0;
		for(int i=0; i<6; i++) cin >> qs[i];//利用空格作为cin的结束符
		string t;
		switch(qs[3][0])//利用第4个单词的首字母来区分
		{
			case 'c':
				if(mp[qs[0]]==qs[5]) res = 1;
				break;//X is a child of Y
			case 'p':
					if(mp[qs[5]]==qs[0]) res = 1;
				break;//X is the parent of Y
			case 's':
				if(mp[qs[0]]==mp[qs[5]]) res = 1;
				break;//X is a sibling of Y
			case 'd':
				t = qs[0];
				while(t!="000" && mp[t]!=qs[5]) t = mp[t];
				if(t!="000") res = 1;
				break;//X is a descendant of Y
			case 'a':
				t = qs[5];
				while(t!="000" && mp[t]!=qs[0]) t = mp[t];
				if(t!="000") res = 1;
				break;//X is an ancestor of Y ????
		}
		if(res) cout << "True\n";
		else cout << "False\n";
	}
	return 0;
}

7-10 狼人杀 (25 分)

题目描述

以下文字摘自《灵机一动·好玩的数学》：“狼人杀”游戏分为狼人、好人两大阵营。在一局“狼人杀”游戏中，1号玩家说：“2号是狼人”，2号玩家说：“3号是好人”，3号玩家说：“4号是狼人”，4号玩家说：“5号是好人”，5号玩家说：“4号是好人”。已知这5名玩家中有2人扮演狼人角色，有2人说的不是实话，有狼人撒谎但并不是所有狼人都在撒谎。扮演狼人角色的是哪两号玩家？

本题是这个问题的升级版：已知 N 名玩家中有 M 人扮演狼人角色，有 L 人说的不是实话，有狼人撒谎但并不是所有狼人都在撒谎。要求你找出扮演狼人角色的是哪几号玩家？

输入格式:
输入在第一行中给出三个正整数 N、M、L，其中 5 ≤ N ≤ 100，2 ≤ M，L < N。随后 N 行，第 i 行给出第 i 号玩家说的话（1 ≤ i ≤ N），即一个玩家编号，用正号表示好人，负号表示狼人。

输出格式:
如果有解，在一行中按递减顺序输出 M 个狼人的编号，其间以空格分隔，行首尾不得有多余空格。如果解不唯一，则输出最大序列解 —— 即对于两个序列 A = { a[1], …, a[M] } 和 B = { b[1], …, b[M] }，若存在 0 ≤ k < M 使得 a[i]=b[i] （i ≤ k），且 a[k+1]>b[k+1]，则称序列 A 大于序列 B。若无解则输出 No Solution。

输入样例 1:

5 2 2
-2
+3
-4
+5
+4

输出样例 1:

4 1

输入样例 2:

6 2 3
-2
+3
-4
+5
+4
-3

输出样例 2（解不唯一）:

6 4

输入样例 3:

6 2 5
-2
+3
-4
+5
+4
+6

输出样例 3:

No Solution

思路

枚举
编号从大到小枚举每一套狼人方案，然后判断这套方案是否满足题目要求，是的话就搞掂
要获得每一套狼人的编号方案，可使用dfs生成

代码

#include<bits/stdc++.h>
using namespace std;
int n, m, l;
int a[101], b[101];
bool judge(int a[], int b[]) { //判断b数组中的m个狼人是否合理
	int tmp[101];//当前方案，1是好人，-1是狼人
	fill(tmp+1, tmp+n+1, 1);//好人
	for(int i=1; i<=m; i++) tmp[b[i]] = -1;//这些是狼人
	int cnt = 0;//根据假设情况，说假话的人数 ?
	int langcnt = 0;//说假话的狼人数量 ?
	for(int i=1; i<=n; i++) { //统计有多少人说假话
		int id = abs(a[i]);
		??
		if(a[i]*tmp[id]<0)//i说的话和假设的实际情况不一致，说明i说假话
			 {
			cnt++;
			if(tmp[i]==-1) langcnt++;//i是狼人
		
		}
	}
	if(cnt==l && langcnt>0 && langcnt<m) return true;//说假话人数正确 且 有狼人 且 不
//	是全部狼人
	else return false;
}
bool dfs(int t) {
	//选出第t个狼人, 其编号写入到b[t]
	串绳子：
	if(t==m+1) { //已选出了m个
		if(judge(a, b)) return true;//这m个狼人满足要求
	} else {
		for(int i=b[t-1]-1; i>=1; i--) { //第t个狼人的候选人编号
			b[t] = i;
			if(dfs(t+1)) return true;
		}
	}
	return false;
}
int main() {
	cin >> n >> m >> l;
	for(int i=1; i<=n; i++) cin >> a[i];
	b[0] = n+1;
	if(!dfs(1)) cout << "No Solution";
	else {
		cout << b[1];
		for(int i=2; i<=m; i++) cout << " " << b[i];
	}
	return 0;
}

7-11 串绳子 (25 分)

题目描述

有若干条绳子需要成一条绳。把两条绳子分别对折就可以套接在一起（见下图）。这样得到的绳子可以作为一条绳子与另一条进行串联。每次串连后，原来两段绳子的长度就会减半。

46293e57-aa0e-414b-b5c3-7c4b2d5201e2.jpg

给定 N 段绳子的长度，求它们能串成的绳子的最大长度。

输入格式:
每个输入包含 1 个测试用例。每个测试用例第 1 行给出正整数 N (2≤N≤10
4
)；第 2 行给出 N 个正整数，即原始绳段的长度，数字间以空格分隔。所有整数都不超过10
4
.

输出格式:
在一行中输出能够串成的绳子的最大长度。结果向下取整，即取为不超过最大长度的最近整数。

输入样例:

8
10 15 12 3 4 13 1 15

输出样例:

14

思路

• 代码一：直接用一个数组存，排序后用a[i] = (a[i]+a[i-1])/2不断更新数组，a[n-1]即为答案
• 代码二：使用小顶堆的优先队列priority_queue<double,vector,greater > q;

知识点

优先队列！！！
c++优先队列(priority_queue)用法详解

//升序队列
priority_queue <int,vector<int>,greater<int> > q;
//降序队列
priority_queue <int,vector<int>,less<int> >q;

//greater和less是std实现的两个仿函数（就是使一个类的使用看上去像一个函数。其实现就是类中实现一个operator()，这个类就有了类似函数的行为，就是一个仿函数类了）

和队列基本操作相同:
top 访问队头元素
empty 队列是否为空
size 返回队列内元素个数
push 插入元素到队尾 (并排序)
emplace 原地构造一个元素并插入队列
pop 弹出队头元素
swap 交换内容

代码一

#include<iostream>
#include<string>
#include<algorithm>
using namespace std;
int main() {
	int n;
	cin >> n;
	int a[10000];
	for(int i=0; i<n; i++) cin >> a[i];
	sort(a, a+n);
	for(int i=1; i<n; i++) a[i] = (a[i]+a[i-1])/2;
	cout << a[n-1];
	return 0;
}

代码二（优先队列）

#include <bits/stdc++.h>
using namespace std;
int main(){
	int n;
	cin>>n;
	priority_queue<double,vector<double>,greater<double> > q;
	for(int i=0;i<n;i++){
		double num;
		cin>>num;
		q.push(num);
	}
	while(q.size()>=2){
		double t1 = q.top();
		q.pop();
		double t2 = q.top();
		q.pop();
		double t3 = t1/2+t2/2;
		q.push(t3);
		
	}
	cout<<floor(q.top());
	
}