1.冒泡算法:N个数,大循环需要进行N-1次,每次找到剩余数中,最大的数;
小循环:从下标为0的数值开始,直到i-1位置(即有序部分的前一个位置)
void BubbleSort(vector<int>& nums)//时间复杂度为:O(n2)
{
int size = nums.size();
for (int i =size-1; i >0; --i)//N个数进行了N-1次大循环,这个只是规定了大循环次数
{
for (int j = 0; j < i; ++j)//每一次小循环从0开始,要到未排序的最后一个元素,刚好就是i
{
if(nums[j]>nums[j+1])
{
swap(num[j],nums[j+1]);
}
}
}
return;
}
2.选择排序
首先在未排序序列中找到最小(大)元素,存放到排序序列的起始位置。
再从剩余未排序元素中继续寻找最小(大)元素,然后放到已排序序列的末尾。
重复第二步,直到所有元素均排序完毕
void SecletSort(vector<int>& nums)
{
for (int i = 0; i < nums.size() - 1; i++) {
int min = i;//暂时认为i位置是最小值
for (int j = i + 1; j < nums.size(); ++j)
if (nums[j] < nums[min])
min = j;
swap(nums[i], nums[min]);
}
}3.插入排序
每次将一个待排序的记录,按其关键字大小插入到前面已经排好序的子文件中的适当位置,直到全部记录插入完成为止。
void InsertSort(vector<int>& nums)
{
int size = nums.size();
if (size < 2)
return;
for (int i = 1; i < size; ++i)//要从1开始
{
int j = i-1;//j初始赋值为i-1,从而让[j]与[j+1]比较,最终当j<0时,循环终止
while (j >= 0)
{
if (nums[j] > nums[j + 1])
{
swap(num[j],nums[j+1]);
}
else
break;
--j;
}
}
}4.希尔排序
第一个突破 O(n2) 的排序算法,是插入排序的改进版。它与插入排序的不同之处在于,它会优先比较距离较远的元素。希尔排序又叫缩小增量排序
void shellSort(vector<int>& nums)
{//分组、组内排序
int size = nums.size();
int i, j, tmp, increment;
for (increment = size / 2; increment > 0; increment /= 2) {//确定间隔,将总数分成increment个组了,也就这接下来要进行increment次循环
//组内排序:方法是插入排序
for (i = increment; i < size; i++) {
tmp = nums[i];
for (j = i - increment; j >= 0 && tmp < nums[j]; j -= increment) {
nums[j + increment] = nums[j];
}
nums[j + increment] = tmp;
}
}
}5.归并排序
-
申请空间,使其大小为两个已经排序序列之和,该空间用来存放合并后的序列;
-
设定两个指针,最初位置分别为两个已经排序序列的起始位置;
-
比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置;
-
重复步骤 3 直到某一指针达到序列尾;
-
将另一序列剩下的所有元素直接复制到合并序列尾
void Merge(vector<int>& nums, int left, int right, int mid)
{
int* p = new int[right - left + 1];
int i = 0, p1 = left, p2 = mid + 1;
while (p1 <= mid && p2 <= right)
{
p[i++] = nums[p1] <= nums[p2] ? nums[p1++] : nums[p2++];
}
while (p1 <= mid)
{
p[i++] = nums[p1++];
}
while (p2 <= right)
{
p[i++] = nums[p2++];
}
for (int i = 0; i < right - left + 1; ++i)
{
nums[left + i] = p[i];
}
delete[] p;
}
void MergeSort(vector<int>& nums, int left, int right)
{
if (left== right)
return;
int mid = left + (right - left) / 2;
MergeSort(nums, left, mid);
MergeSort(nums, mid + 1, right);//递归成一小段一小段的,重点的比较,放置在merge中进行
Merge(nums, left, right, mid);
}?6.快速排序
-
从数列中挑出一个元素,称为 "基准"(pivot);
-
重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面,所有元素与基准值相等的不动。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
-
递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序;
vector<int> partition(vector<int>& nums,int left,int right)
{
int less = left - 1;//初始时小于区右边界
int more = right;//初始时大于区左边界
while (left < more)
{
if (nums[left] < nums[right])
swap(nums[left++], nums[++less]);
else if (nums[left] > nums[right])
swap(nums[left], nums[--more]);
else
left++;
}
swap(nums[right], nums[more]);
return vector<int>({ less+1,more });
}
void QuickSort(vector<int>& nums, int left, int right)
{
if (left < right)
{
srand((unsigned)time(NULL));
int temp = (rand() % (right-left + 1)) + left;
swap(nums[temp], nums[right]);
//要取得[a,b)的随机整数,使用(rand() % (b-a))+ a;
//要取得[a, b]的随机整数,使用(rand() % (b - a + 1)) + a;
//要取得(a, b]的随机整数,使用(rand() % (b - a)) + a + 1;
//通用公式:a + rand() % n;其中的a是起始值,n是整数的范围。
auto p=partition(nums, left, right);
QuickSort(nums, left, p[0] - 1);
QuickSort(nums, p[1] + 1,right);
}
}?7.堆排序
主要是通过堆的上浮和下沉操作来实现的。
void HeapInsert(vector<int>& nums, int index)//O(logN)
{
while (nums[index] > nums[(index - 1) / 2])
{
swap(nums[index], nums[(index - 1) / 2]);
index = (index - 1) / 2;
}
}
void Heapify(vector<int>& nums, int index, int heapsize)//index是从哪个位置开始做下沉操作,heapsize确定左孩子和右孩子的边界
//O(logN)
{
int left = 2 * index + 1;
while (left < heapsize)
{
//左右孩子争,确定较大的值的下标
int largest = left + 1 < heapsize && nums[left + 1] > nums[left] ? left + 1 : left;
//大孩子与父亲比较
largest = nums[index] > nums[largest] ? index : largest;
if (index == largest)
break;
swap(nums[index], nums[largest]);
index = largest;
left = 2 * index + 1;
}
}
void HeapSort(vector<int>& nums)
{
if (nums.size() < 2)
return;
//建立大根堆的过程,可以通过HeapInsert插入,时间复杂度为O(NlogN)
for (int i = 0; i < nums.size(); ++i)//O(N)
{
HeapInsert(nums, i);//O(logN)
}
//更简单的建立大根堆的方法,复杂度只有O(N),从叶节点开始做下沉操作
/*for (int i = nums.size() - 1; i >= 0; --i)
{
Heapify(nums, i, nums.size());
}*/
int heapsize = nums.size();
swap(nums[0], nums[--heapsize]);//O(logN)
while (heapsize > 0)//O(N)
{
Heapify(nums, 0, heapsize);//O(logN)
swap(nums[0], nums[--heapsize]);
}
}8.计数排序
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为 i 的元素出现的次数,存入数组 C 的第 i 项;
- 对所有的计数累加(从 C 中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第 C(i) 项,每放一个元素就将 C(i) 减去 1。
void CountingSort(vector<int>& nums)
{
int maxvalue = *max_element(nums.begin(), nums.end());
int* p = new int[maxvalue + 1]{};//建立从0到maxvalue个桶
for (auto i : nums)
p[i]++;//模拟哈希表
int i = 0;
for (int j = 0; j < maxvalue + 1; ++j)//依次输出这maxvalue+1个桶
while (p[j] != 0)//当次数为0时跳出循环
{
nums[i++] = j;
p[j]--;
}
}?9.桶排序
桶排序是计数排序的升级版。它利用了函数的映射关系,高效与否的关键就在于这个映射函数的确定。为了使桶排序更加高效,我们需要做到这两点:
- 在额外空间充足的情况下,尽量增大桶的数量
- 使用的映射函数能够将输入的 N 个数据均匀的分配到 K 个桶中
同时,对于桶中元素的排序,选择何种比较排序算法对于性能的影响至关重要。
映射函数将元素进桶:
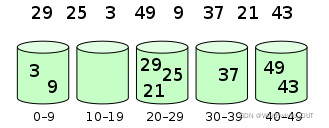
?桶内元素排序
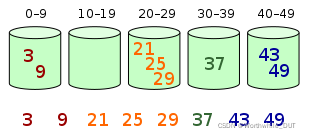
10.基数排序
基数排序(Radix Sort)是按照低位先排序,然后收集;再按照高位排序,然后再收集;依次类推,直到最高位。有时候有些属性是有优先级顺序的,先按低优先级排序,再按高优先级排序。最后的次序就是高优先级高的在前,高优先级相同的低优先级高的在前。
int maxbits(vector<int>& nums)
{
int maxvalue = INT_MIN;
for (auto i : nums)
{
maxvalue=max(maxvalue, i);
}
int res = 0;
while (maxvalue!=0)
{
maxvalue /= 10;
++res;
}
return res;
}
int getdigit(int m, int n)
{
int ans = 0;
while (n >= 0)
{
ans = m % 10;
m /= 10;
--n;
}
return ans;
}
void RadixSort(vector<int>& nums)
{
int digit = maxbits(nums);//1.确定数组中的最大位数,从而确定大循环入桶-出桶次数
int* bucket = new int[nums.size()]();//2.建立等效空间的数组来模拟队列桶
int i = 0, j = 0;
for (int d = 0; d < digit; ++d)
{
vector<int> count(10);//建立计数数组
for (auto i : nums)//将每个数组按照个、十、百的顺序分别往计数数组中计数
{
j = getdigit(i, d);
count[j]++;
}
for (i=1; i < 10; ++i)//计数数组改为前缀数组
{
count[i] += count[i - 1];
}
for (i = nums.size() - 1; i >= 0; --i)//逆序放桶,通过获得每个数的数位,索引到
//前缀数组中的该元素在等效数组中的位置,从而放入等效数组中,并将count计数调整
{
j = getdigit(nums[i], d);
bucket[count[j] - 1] = nums[i];
count[j]--;
}
for (i = 0; i < nums.size();++i)//等效数组复制到原数组中,作为第一次大循环结束
{
nums[i] = bucket[i];
}
}
}