[数据结构与算法]2021 ICPC Asia Jinan Regional Contest-J Determinant（取模高斯消元）

题面链接

https://pintia.cn/market/item/1459833348620926976

题面

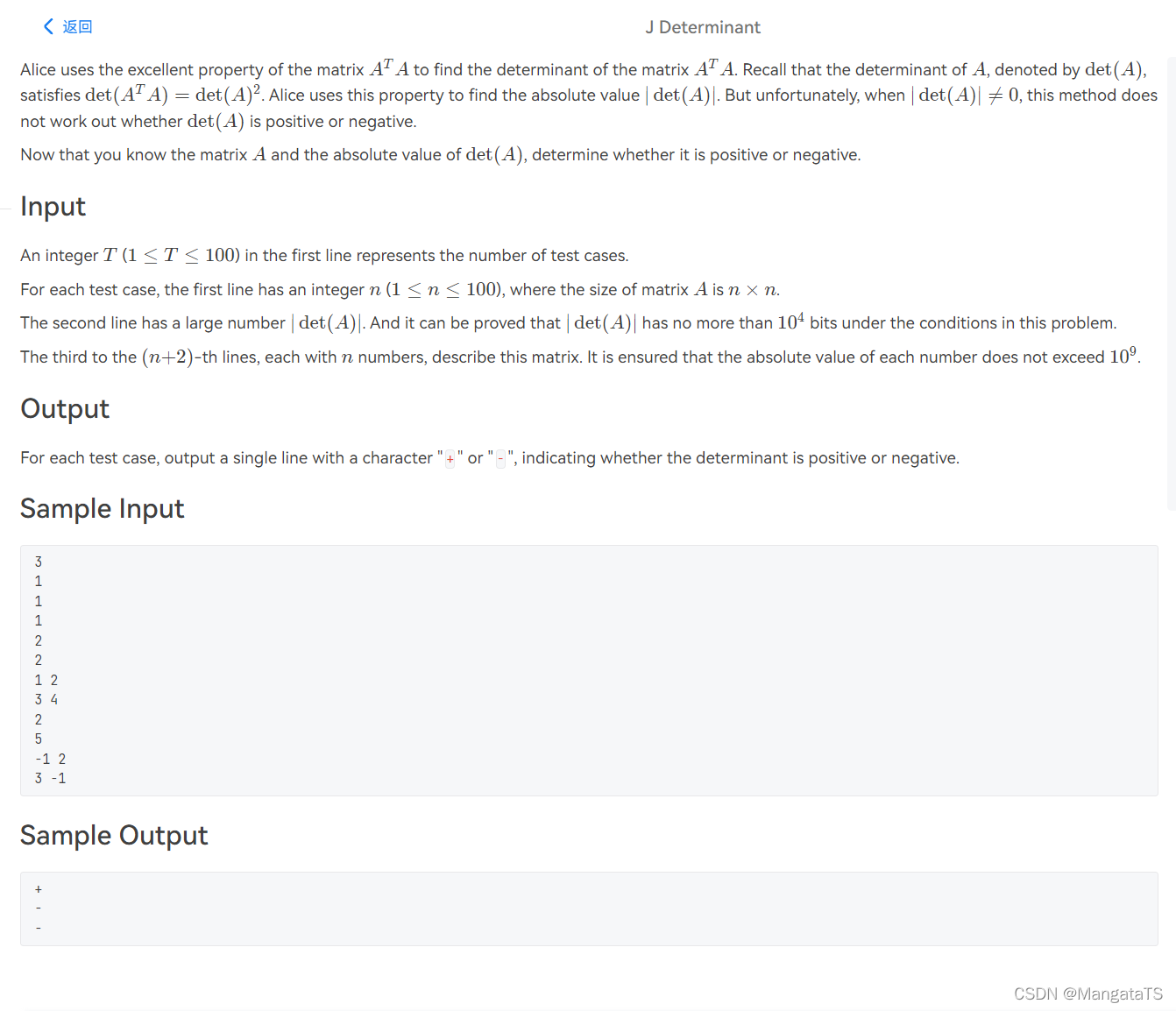
题意

给你一个 $n\times n$ 的矩阵，并给你一个长度为 $10^4$ 以内的 $delt$ 表示行列式的绝对值，然后我们要求这个矩阵的行列式的值的正负性，如果是正数的话就输出+否则输出-

思路

其实就是普通的高斯消元，只不过多了一个取模操作，因为 $delt$ 的数据很大，并且如果用浮点类型的话会溢出以及精度问题，于是我们需要自己选择一个模数（素数），这里我选的是$10^9+7$ 然后，我们将读到的 $delt$ 不断取模，然后在跑一次取模高斯消元最后只需要判断行列式的值是否和我们读入的 $delt$ 相同即可，因为我们读入的是一个绝对值，如果当我们计算出的行列式的值是一个负数，由于我们有取模的操作那么肯定会使得其绝对值和负数加上模数后的值不同，而对于高斯消元的操作其实可以参考这个：https://acmer.blog.csdn.net/article/details/122932692

代码

#include<bits/stdc++.h>
using namespace std;
#define ll long long
#define mod 1000000007
#define endl "\n"
#define PII pair<int,int>
#define INF 0x3f3f3f3f

const int N = 1e2+10;

ll n,a[N][N],delt;

ll ksm(ll a,ll b){
	ll ans = 1;
	while(b){
		if(b & 1) ans = ans * a % mod;
		b >>= 1;
		a = a * a % mod;
	}
	return ans;
}

ll inv(ll x){
	return ksm(x,mod-2);
}

void guss(){
	ll ans = 1LL;
	for(int i = 1;i <= n; ++i) {//枚举当前处理到第几列
		for(int j = i;j <= n; ++j) {//找到一个第i列不为空的行
			if(a[j][i]) {
				for(int k = i;k <= n; ++k) //交换i,j行
					swap(a[i][k],a[j][k]);
				if(i != j) ans = -ans;
				break;
			}
		}
		if(!a[i][i]) return ;
		//这里就是将第i行下面所有行的第i列清空，变成一个阶梯型的矩阵
		for(ll j = i + 1,iv = inv(a[i][i]);j <= n; ++j) {
			ll t = a[j][i] * iv % mod;
			for(ll k = i;k <= n; ++k) {
				a[j][k] = (a[j][k] - t * a[i][k] % mod + mod) % mod;
			}
		}
		//处理完第i行下面的所有行，于是我们将其a[i,i]乘在ans中
		ans = (ans * a[i][i] + mod) % mod;
	}
	//如果说我们通过取模计算的结果和delt相同，那么就说明矩阵的行列式是正的
	//因为如果是负数的话由于我们算的是行列式，而delt给的是行列式的绝对值，那么肯定会有不同
	if(ans == delt) cout<<"+"<<endl;
	else cout<<"-"<<endl;
}

int main()
{
	ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
	string s;
	int t;
	cin>>t;
	while(t--){
		cin>>n>>s;
		delt = 0LL;
		for(int i = 0,l = s.size();i < l; ++i) {
			delt = (delt * 10LL + s[i] - '0') % mod;
		}
		for(int i = 1;i <= n; ++i) 
			for(int j = 1;j <= n; ++j)
				cin>>a[i][j];
		guss();
	}
	

	return 0;
}