[数据结构与算法]Leetcode--Java--547. 省份数量

题目描述

有 n 个城市，其中一些彼此相连，另一些没有相连。如果城市 a 与城市 b 直接相连，且城市 b 与城市 c 直接相连，那么城市 a 与城市 c 间接相连。

省份 是一组直接或间接相连的城市，组内不含其他没有相连的城市。

给你一个 n x n 的矩阵 isConnected ，其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连，而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。

样例描述

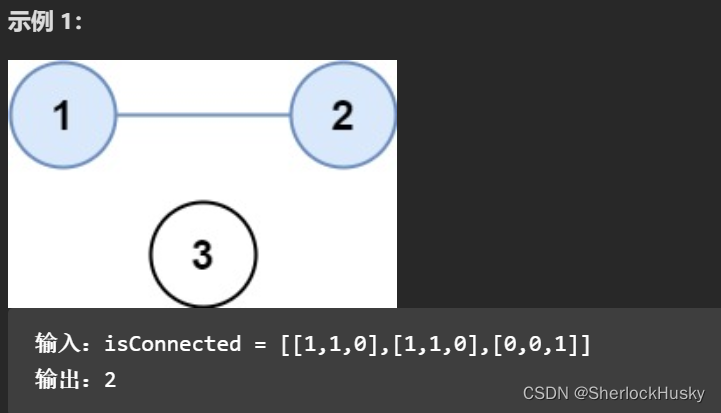
思路

图论 + 连通图 + DFS/BFS/并查集
求无向图中联通域个数
方法一：DFS遍历每个连通块的数目，设置标记数组，只要没访问过就为一个新的连通域，然后dfs去将该区域的所有点标记为访问
方法二：BFS，思路同一
方法三：并查集
首先默写并查集的基础模板
初始化设置自己的父结点是自身
对于任意两个结点，如果是连接的，就的合并成一个集合
最后判断父结点集合，如果还是自身，说明是一个连通块的父结点，统计起来就是个数

代码

DFS：

class Solution {
    boolean vis[];
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        int res = 0;
        vis = new boolean[n];
        for (int i = 0; i < n; i ++ ) {
            //没访问过，说明是新的连通块
            if (!vis[i]) {
                res ++;
                //dfs遍历该连通块的所有结点
                dfs(i, isConnected);
            }
        }
        return res;
    }
    public void dfs(int i, int [][]isConnected) {
        int n = isConnected.length;
        for (int j = 0; j < n; j ++ ) {
            //有路径并且没访问过
            if (isConnected[i][j] == 1 && !vis[j]) {
                vis[j] = true;
                dfs(j, isConnected);
            }
        }
    }
}

BFS

class Solution {
    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        boolean vis[] = new boolean[n];
        Deque<Integer> queue = new LinkedList<>();
        int res = 0;
        for (int i = 0; i < n; i ++ ) {
            if (!vis[i]) {
                res ++;
                vis[i] = true;
                queue.offer(i);
                while (!queue.isEmpty()) {
                    int w = queue.poll();
                    for (int j = 0; j < n; j ++ ) {
                        if (isConnected[w][j] == 1 && !vis[j]) {
                            vis[j] = true;
                            queue.offer(j);     
                        }
                    }
                }
            }
        }    
        return res;   
    }
}

并查集

class Solution {
    int p[];
    //查询父结点
    public int find(int x) {
        if (x != p[x]) {
            p[x] = find(p[x]);
        }
        return p[x];
    }
    //合并
    public void union(int x, int y) {
        int fx = find(x);
        int fy = find(y);
        if (p[fx] != fy) {
            p[fx] = fy;
        }
    }

    public int findCircleNum(int[][] isConnected) {
        int n = isConnected.length;
        p = new int[n];
        //初始化并查集，将父结点设置为自己
        for (int i = 0; i < n; i ++ ) {
            p[i] = i;
        }
        //枚举任意两个结点，只要是连接的（在同一个连通域）
        for (int i = 0; i < n; i ++ ) {
            for (int j = 1; j < n; j ++ ) {
                if (isConnected[i][j] == 1) {
                    union(i, j);
                }
            }
        }
        int res = 0;
        //遍历父结点集，如果还是本身，说明就是该连通领域的父结点
        for (int i = 0; i < n; i ++ ) {
            if (p[i] == i) {
                res ++;
            }
        }
        return res;

    }
}