摘要:
本文研究了在秩最多为r的n×m矩阵集上使一般目标函数f(X)最小化的一般秩约束优化问题。为了解决秩约束并减少计算负担,我们将X分解为UVT,其中U和V分别是n×r和m×r矩阵,然后对小矩阵U和V进行优化。我们描述的全局非凸分解问题的优化几何,表明相应的目标函数满足鲁棒严格的鞍属性robust strict saddle property 只要原始目标函数f满足限制强凸性restricted strong convexity和平滑特性smoothness properties,确保全局收敛的许多局部搜索算法(如噪声梯度下降)在多项式时间解决分解问题。我们还提供了一个矩阵分解问题的优化几何的全面分析,我们的目标是找到n×r和m×r矩阵U和V,使UVT近似于给定的矩阵X*。除了鲁棒严格鞍性质外,我们证明了矩阵分解问题的目标函数没有伪局部极小值spurious local minima,并且不仅在rank(X?*?)= r的精确参数化情况下服从严格鞍性质,也对于过参数化的情况rank(X?*?)<?r和欠参数化的情况下rank(X?*?)>r.这些几何性质表明,许多迭代优化算法(如梯度下降)收敛到一个具有随机初始化的全局解。
-
INTRODUCTION
低秩矩阵在科学和工程中广泛应用,包括量子层析扫描[1]、信号处理[2]、机器学习[3]、[4]等;参见[5]的综述。在所有这些设置中,我们经常遇到以下秩约束优化问题:
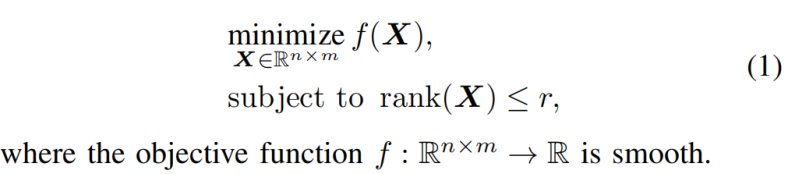
无论目标函数f是凸的还是非凸的,秩约束使(1)的低秩矩阵优化?高度非凸,在一般的[6]【Rank minimization and applications in system theory】中 从计算复杂度方面上讲是NPhard。通过替换涉及核范数的秩约束,将(1)转化为凸问题,已经付出了大量的努力。该策略已被广泛应用于矩阵逆问题[7],产生于信号处理[5]、机器学习[8]和控制[6]中。利用凸分析技术,证明了核范数最小化在恢复低秩矩阵[9]方面具有最优的性能。然而,尽管性能最优,求解核范数最小化是非常昂贵的计算,即使使用专门的一阶算法。例如,奇异值阈值化算法[10]需要在每次迭代中执行昂贵的奇异值分解(SVD),这使得它在大规模设置中无法进行计算。这就防止了核规范最小化扩展到实际问题。
为了缓解计算瓶颈,最近的研究提出将变量分解为X=UVT,并对n × r和m× r
矩阵U和V进行优化,而不是n×m的矩阵X。然后通过因式分解自动满足(1)中的秩约束。这种策略通常被称为?钻机-蒙泰罗型分解Burer-Monteiro type decomposition?,在作者在写了[11],[12]后。在(1)中插入X的参数化,我们可以将程序重铸为以下程序:
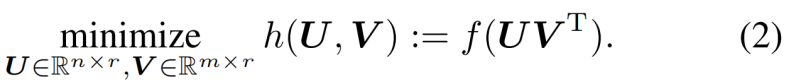
参数化的双线性性质使得(2)的目标函数成为非凸的。因此,它可能会有虚假的局部极小值(即,不是全局极小值的局部极小值),甚至是鞍点。然而,随着分析非凸函数景观的技术创新,最近的一些研究表明,在某些矩阵逆问题中,被分解的目标函数h(U,V)没有虚假的局部最小值[13]-[15]。