[数据结构与算法]算法提高 [蓝桥杯]

1 打包

二分

思路：二分，因为打包的最大重量必然落在 maxWeight 和 sumWeight之间，所以可以二分枚举重量使得恰好可以满足M个包裹。与跳石头这道题类似。

#include<bits/stdc++.h>
using namespace std;

int N, M;
int w[100010];
int sum;
int ma;
int main(){
	cin>>N>>M;
	for(int i = 1; i <= N; ++i){
		cin>>w[i];
		ma = max(w[i], ma);
		sum += w[i];
	}
	//打包的最大重量必然落在 maxW 和 sum之间。 
	int l = ma;
	int r = sum;
	int mid;
	int cnt, cur;
	while(l <= r){
		mid = (l+r)/2;
		cnt = 0;
		cur = 0;
		//统计打包最大重量为mid时的包裹数量。 
		for(int i = 1 ; i <= N; ){
			cur += w[i];
			if(cur > mid){
				cur = 0;
				cnt++;
			}else{
				++i;
				if(i > N){ // 当i>N后却没有达到mid重量，也算一次包裹，不能遗漏
					cnt++;
				}
			}
		}
		if(cnt > M){  //注意  l = mid + 1 的地方不取等号。 
			l = mid + 1;
		}else{
			r = mid - 1;
		}
	}
	cout<<l;
	
	
	return 0;
}

2 约数个数

思维题

思路：思维题，找到规律就非常简单，找不到就只能暴力得部分分，难得要死，就像 平面切分、砝码称重这些题 一样 考思维。n/i表示，i是n/i个数的因数。

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
ll mod = 1000000007;
int n;
int main(){

	cin>>n;
	ll res = 0;
	for(int i = 1; i <= n ; ++i){
		res = (res + n/i) % mod;
		
	}
	cout<<res;
	
	return 0;
}

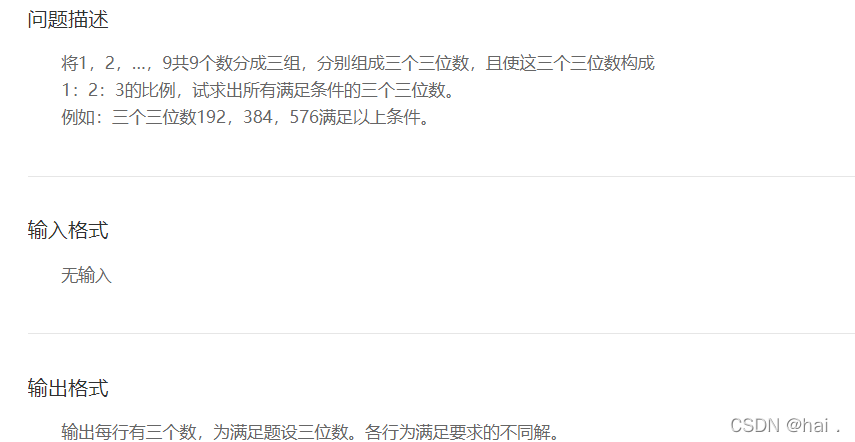
3 寻找三位数

暴力手段

思路：暴力全排列即可。

#include<bits/stdc++.h>
using namespace std;

int a[] = {1,2,3,4,5,6,7,8,9};

int main(){
	do{
		int a1 = a[0]*100+a[1]*10+a[2];
		int b = a[3]*100+a[4]*10+a[5];
		int c = a[6]*100+a[7]*10+a[8];
		if(b)
		if(2*a1 == b && 2*c == 3 * b){ //避免使用 / 
			cout<<a1<<" "<<b<<" "<<c<<endl;
		}
	}while(next_permutation(a,a+9));  // 找下一个全排列
	return 0;
}

4 第二点五个不高兴的小明

动态规划

思路：首先一看这道题就是动态规划，再看数据集范围在1000以内，大概率都是动态规划了，满足最优子结构。

1. 找状态方程，小明从0跳到 n + 1，只能条 t次，由此可以用

dp[i][j]:小明跳到第i个格子所用次数为j的最大权值和。

2. 找状态转移方程，小明可以从第i-1、i-2、…、i-k个格子经过一次跳跃到第i个格子，题目要我们求最大的，因此在里面取max就可以。

dp[i][j] =  max(dp[i-1][j-1],dp[i-2][j-1],...,dp[i-k][j-1])+a[i];
// 将它转到循环中，就是下面这样。
dp[i][j] = max(dp[i][j], dp[i-k][j-1] + a[i]);

3. 初始化，由于权值可能是负的，所以初始值全部要为负无穷，这样才能正确找到max。其次，前p个格子都可以跳1次到达，因此有下面代码中的初始化。

#include<bits/stdc++.h>
using namespace std; 
int n, p , t;
int a[1003];
int dp[1003][1003];  // dp[i][j] 跳了i格用了j次。 
int main(){
	cin>>n>>p>>t;
	// 128 代表 32个1，32个1是int的 负的最大值。
	memset(dp,128,sizeof(dp));
	for(int i = 1 ;i <= n ; ++i){
		cin>>a[i];
		if( i <= p)  //前p个格子都可以跳1次到达
			dp[i][1] = a[i]; 
		
	}
	for(int i = 2; i <= n+1; ++i){
		
		for(int j = 2; j <= t && j <= i; ++j){
			
			for(int k = 1; k <= p && k < i; ++k) // 因为要i-k > 0， 所以必须k < i 。
				dp[i][j] = max(dp[i][j], dp[i-k][j-1] + a[i]);
		}
	}
	cout<<dp[n+1][t];
	return 0;
}