[数据结构与算法]背包问题（贪心）

题目描述

给定一个载重量为M的背包，考虑n个物品，其中第i个物品的重量 ，价值wi （1≤i≤n），要求把物品装满背包，且使背包内的物品价值最大。
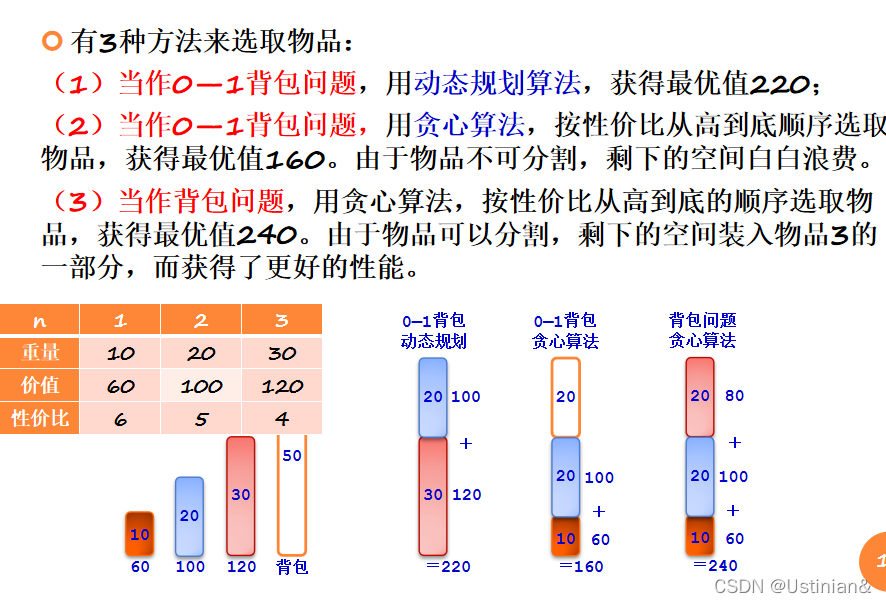
有两类背包问题（根据物品是否可以分割， 如果物品不可以分割，称为0—1背包问题（动态规划)； 如果物品可以分割，则称为背包问题（贪心算法）。

题解思路

数据结构
struct bag{
	int w;			//物品的重量
	int v;			//物品的价值
	double c;		//性价比
}a[1001];			//存放物品的数组

排序因子（按性价比降序）：
bool cmp(bag a, bag b){
	return a.c >= b.c;
}

使用标准模板库函数排序（最好使用stable_sort()函数，
在性价比相同时保持输入的顺序）：
sort(a, a+n, cmp);

计算背包问题的贪心算法

//形参n是物品的数量，c是背包的容量M，数组a是按物品的性价比降序排序
double knapsack(int n, bag a[], double c)
{
　　double cleft = c;　　　　　　　　//背包的剩余容量
　　int i = 0;
　　double b = 0;　　　　　　　　　　//获得的价值
　　//当背包还能完全装入物品i
　　while(i<n && a[i].w<cleft)
　　{
　　　　cleft -= a[i].w;
　　　　b += a[i].v;
　　　　i++;
　　}
　　//装满背包的剩余空间
　　if (i<n) b += 1.0*a[i].v*cleft/a[i].w;
　　return b;
}

计算背包问题的贪心算法，同时得到解向量

如果要获得解向量，则需要在数据结构中加入物品编号：
struct bag{
	int w;
	int v;
	double x;		//装入背包的量，0≤x≤1
	int index;		//物品编号
	double c;
}a[1001];

double knapsack(int n, bag a[], double c)
{
　　double cleft = c;
　　int i = 0;
　　double b = 0;
　　while(i<n && a[i].w<=cleft)
　　{
　　　　cleft -= a[i].w;
　　　　b += a[i].v;
　　　　//物品原先的序号是a[i].index，全部装入背包
　　　　a[a[i].index].x = 1.0;
　　　　i++;
　　}
　　if (i<n)　{
　　　　a[a[i].index].x = 1.0*cleft/a[i].w;
　　　　b += a[a[i].index].x*a[i].v;
　　}
　　return b;
}