[数据结构与算法]【数据结构—图论】图的遍历（DFS、BFS)

图的遍历（DFS、BFS)

关于图的遍历

1.从图的某个顶点出发，访问图中所有顶点，且使每个顶点恰被访问一次的过程被称为图的遍历。
2.图中可能存在回路，且图的任一顶点都可能与其他顶点相通，在访问完某个顶点之后可能会沿着某些边又回到了曾经访问过的顶点。
3.为了避免重复访问，可设置一个标志顶点是否被访问过的辅助数组vis[ ]，它的初始状态为0，在图的遍历过程中，一旦某一个顶点i被访问，就立即让**vis[i]**为1，防止其被多次访问。

两种遍历算法都需要vis[ ]数组来标记是否访问过某个顶点！！

图的深度优先遍历（Depth First Search—DFS）

注意：图深度优先遍历的次序不唯一！

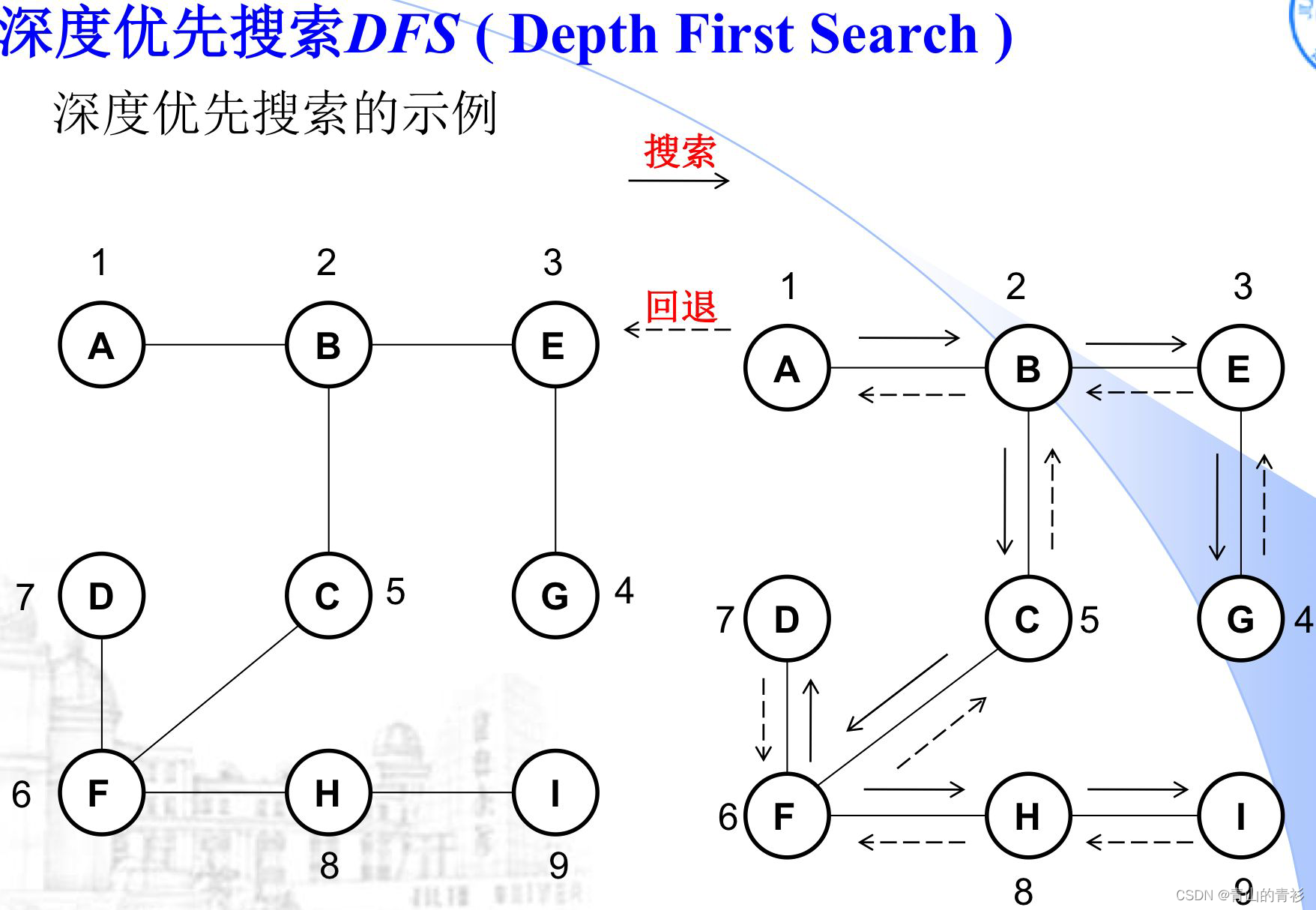
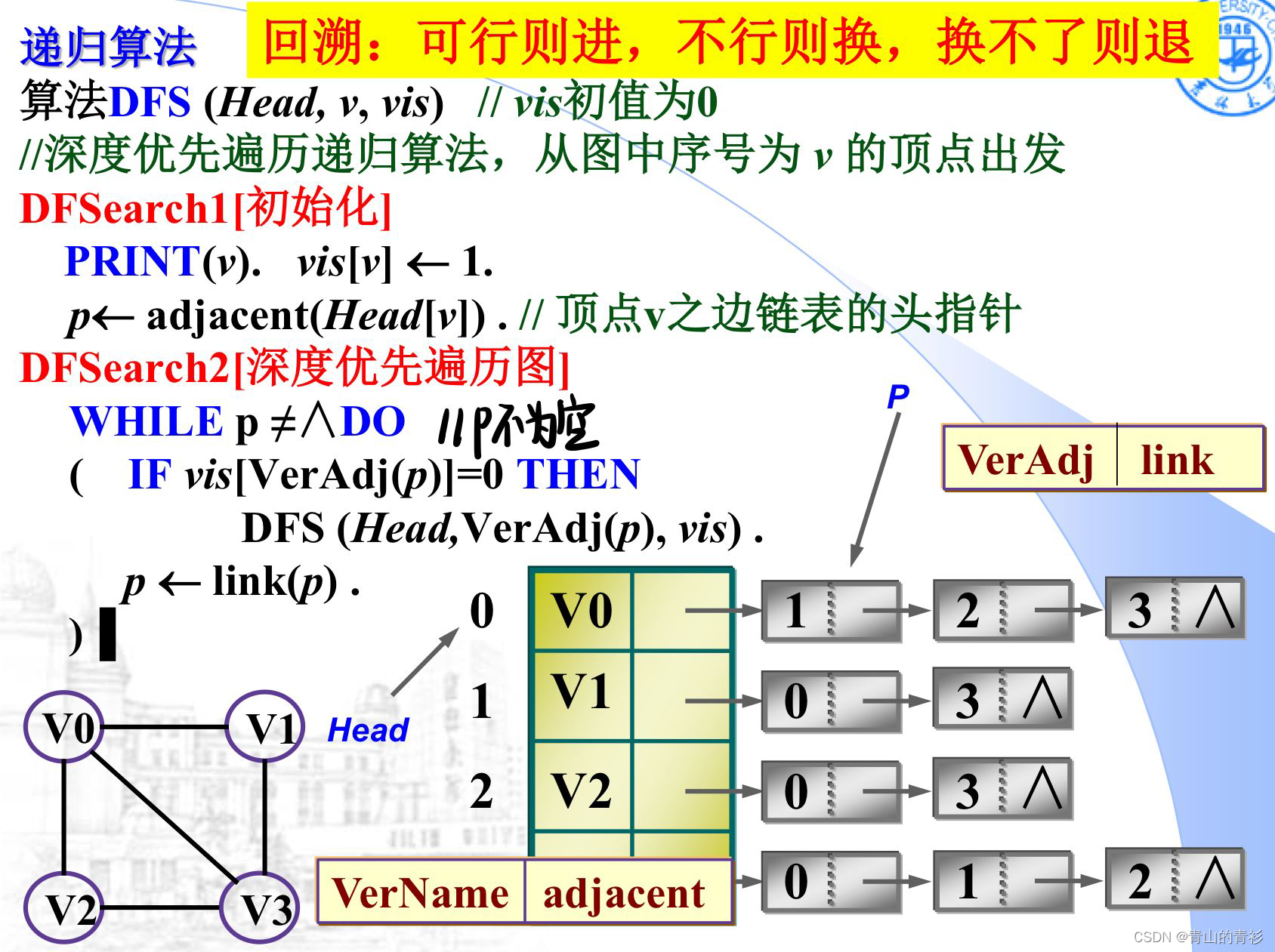
DFS递归算法

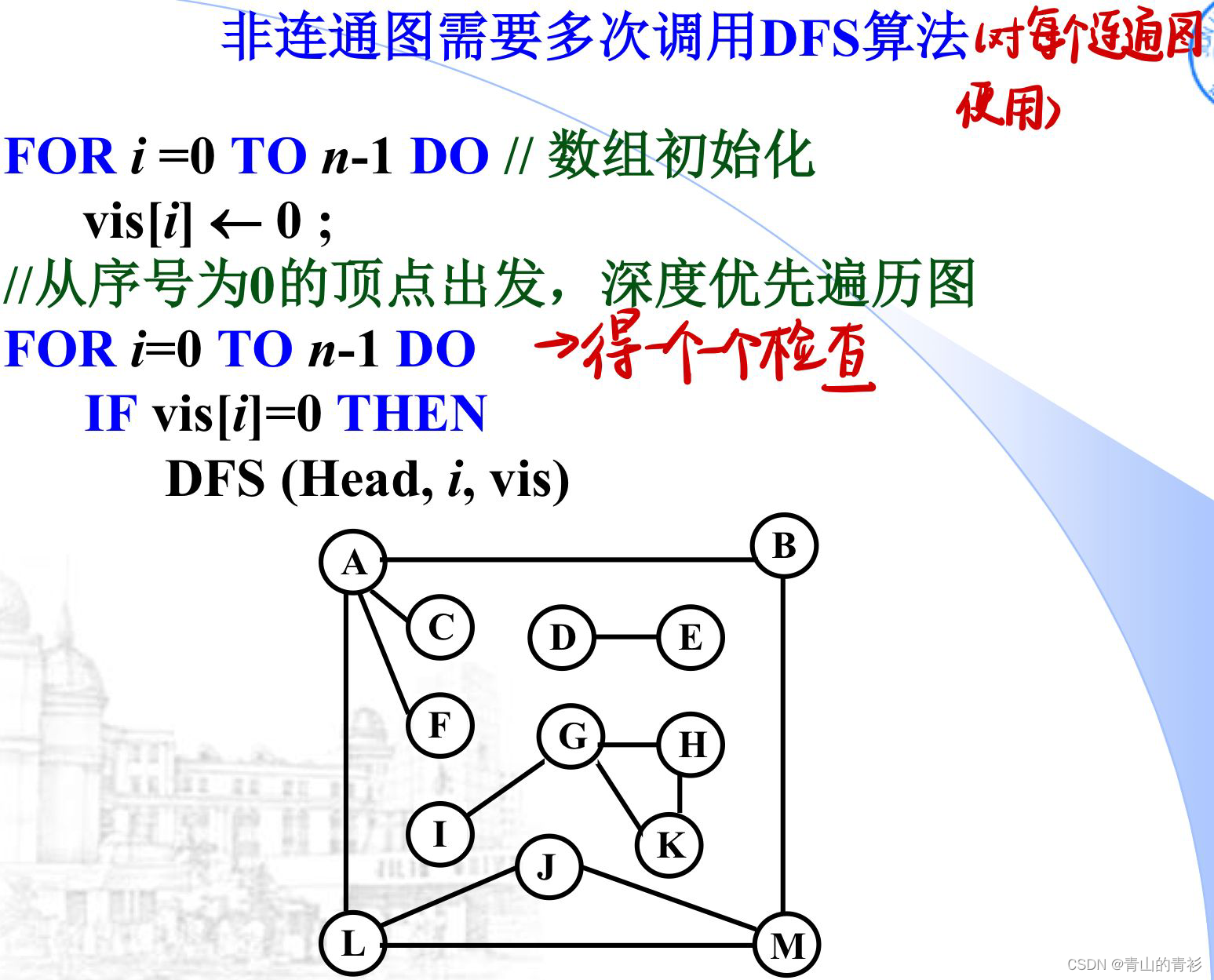
非连通图

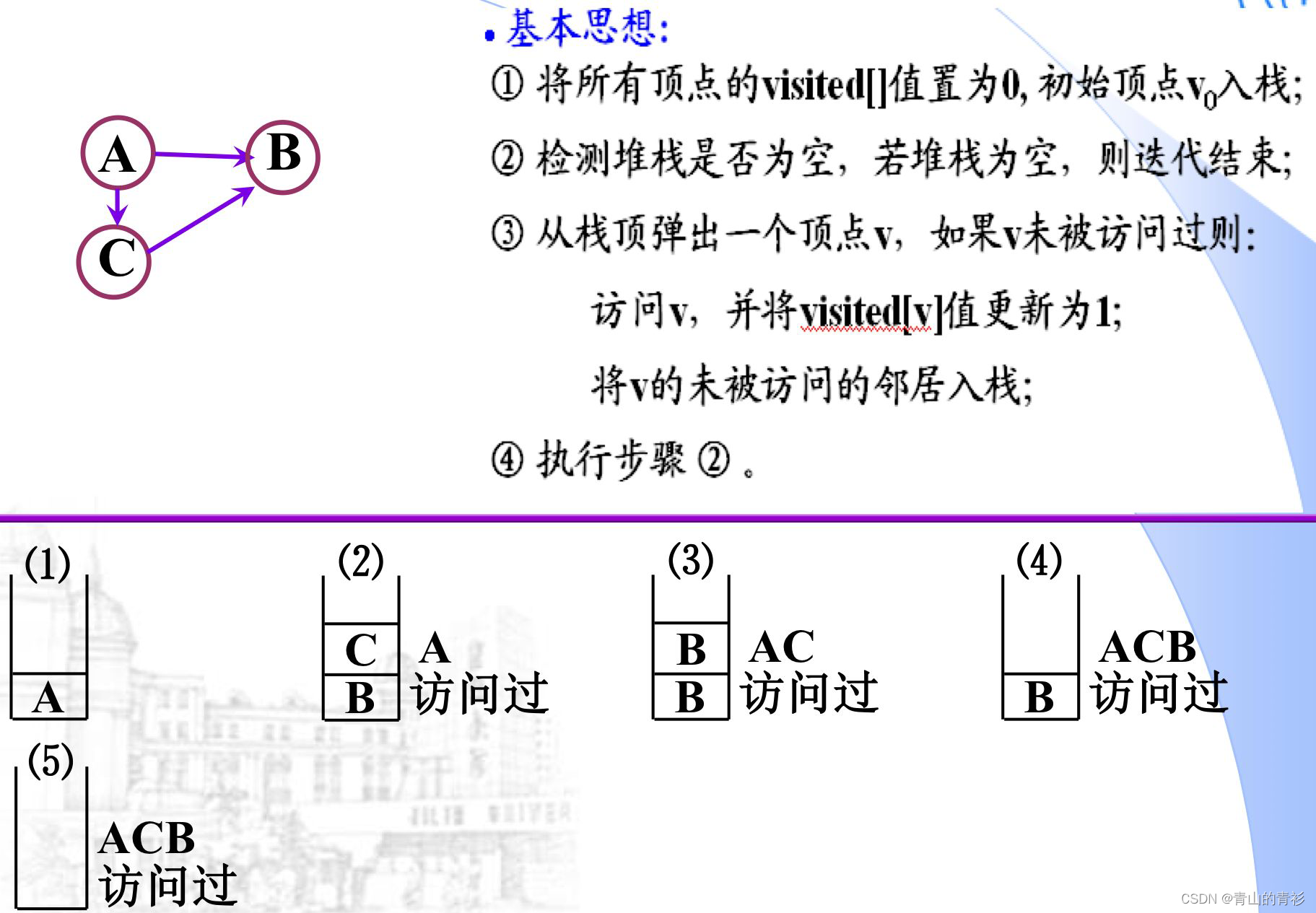
DFS的迭代算法（需要借助栈）

例1：
例2：

图的广度优先遍历（Breadth First Search—BFS）

BFS介绍：

示例：

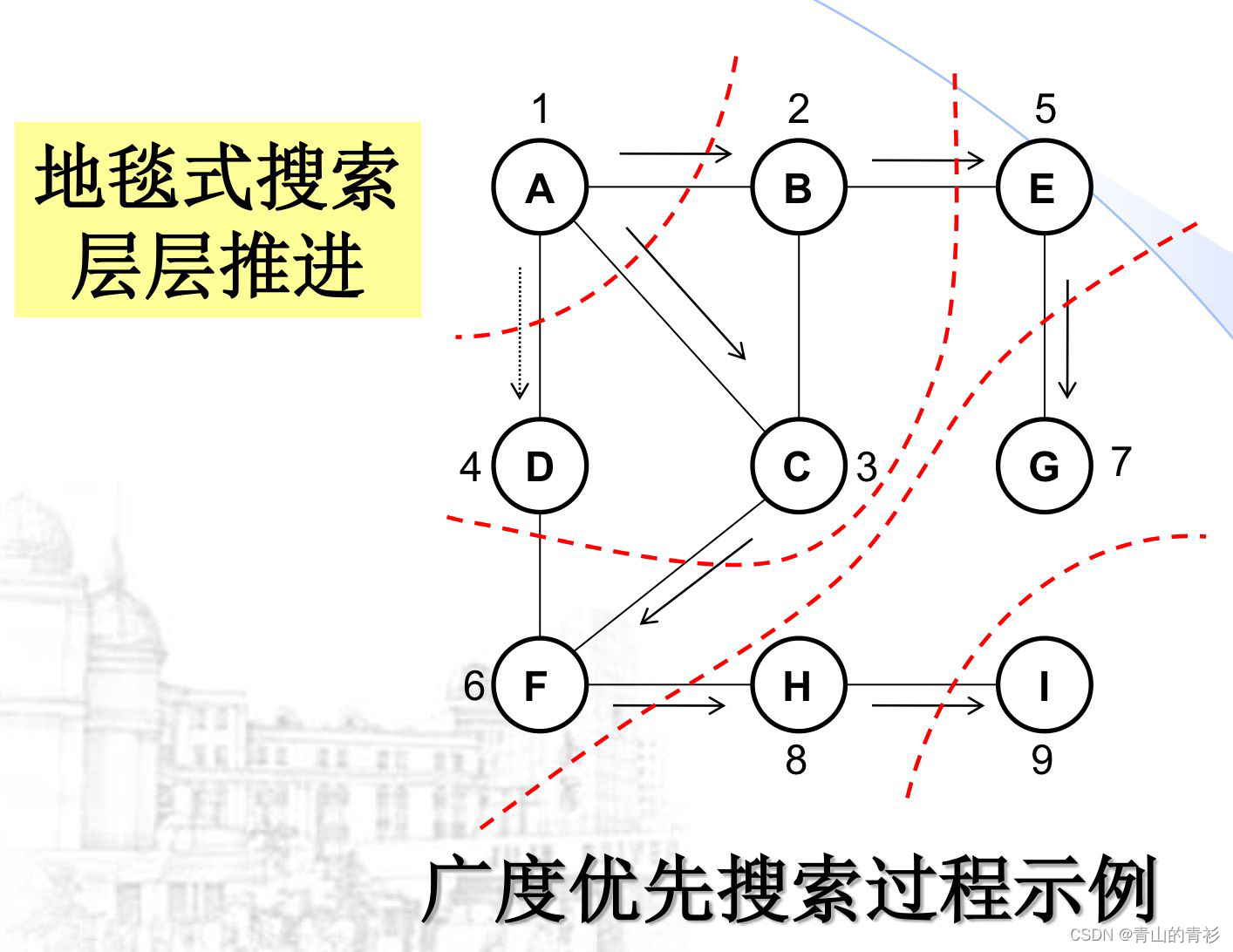
广度优先遍历（BFS）类似于树的层次遍历，是一种分层的搜索过程，每前进一层就访问一批顶点，而不像深度优先搜索（DFS）那样需要回溯。因此，广度优先搜索不是一个需要递归的过程。

这也就是为什么深度优先搜索的迭代算法需要用到栈，而广度优先搜索为了实现逐层访问并记忆未被处理的节点，用到的是队列！

ADL伪代码：

举例：

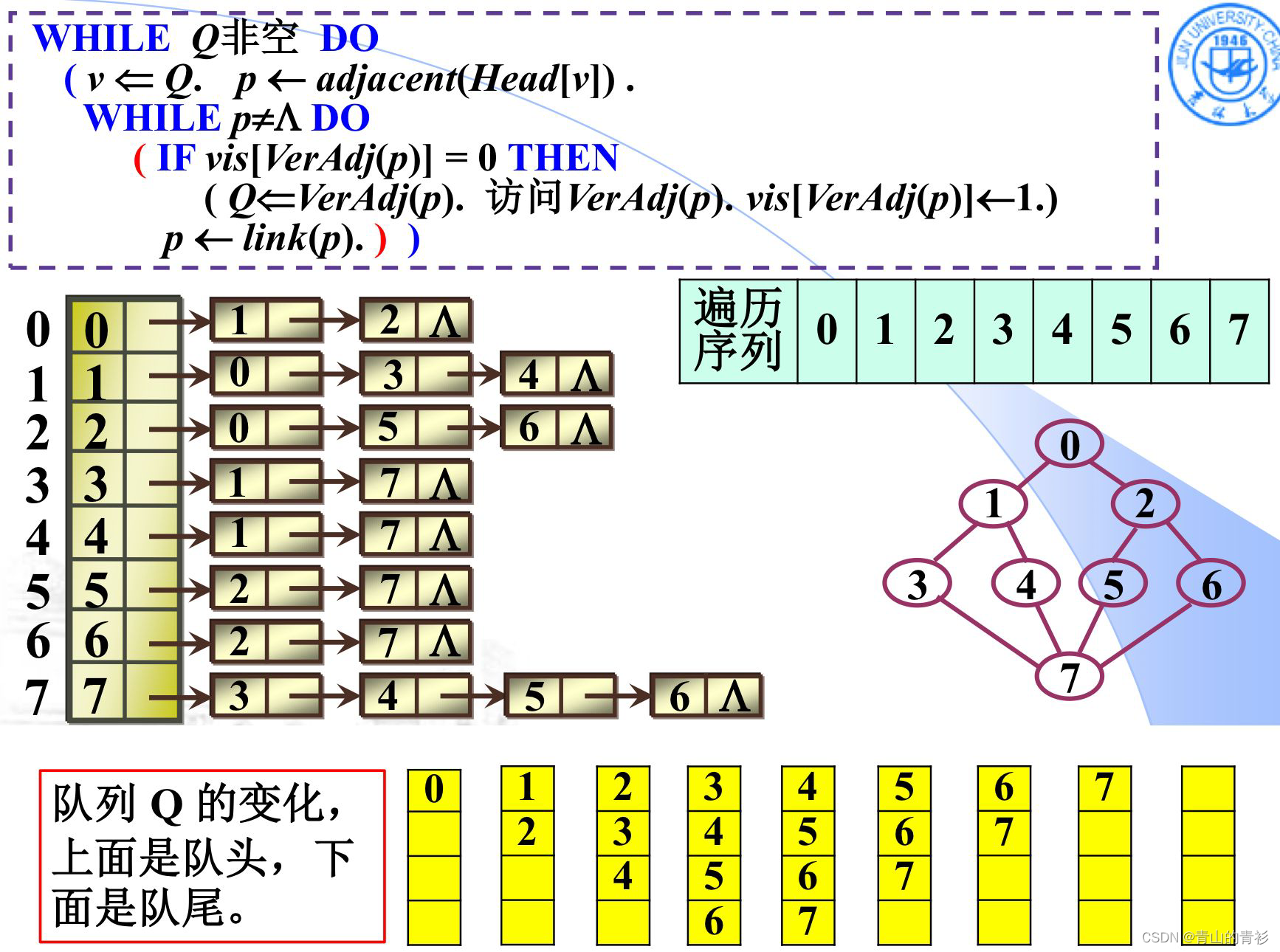
代码实现

//图的结构
//边结点的结构
typedef struct Edge
{
    int Veradj;//邻接顶点序号
    struct Edge* link;//指向下一个边结点的指针 struct Edge*指向他自己！
}Edge, * ArcNode;

//顶点表中结点的结构
typedef struct Vertex
{
    int Vername;//顶点名称
    Edge* adjacent;//边链表的头指针  //指向edge
}Vertex;

//邻接表的结构
typedef struct LGraph {
    Vertex vertices[200]; //顶点表 它包含Vertex这个结构体
}ALGraph;

ALGraph G;

//BFS
void BFS(int n, int m, SqQueue& Q, int a, int b)//a为起点 b为终点
{
    ArcNode q;  //指向边链表的指针
    int v;
    for (int i = 0; i < n; i++)  dist[i] = -1;
    dist[a] = 0;
    EnQueue(Q, a);
    while (!QueueEmpty(Q)) {
        v = DeQueue(Q);//队头顶点v出队！！
        q = G.vertices[v].adjacent;
        while (q != NULL)
        {
            int w = q->Veradj;
            if (dist[w] == -1) //未被访问过
            {
                dist[w] = dist[v] + 1;
                EnQueue(Q, w);
            }
            q = q->link;
        }
    }//执行结束
}