[数据结构与算法]采用动态规划思维求解数塔问题，c++实现

数塔问题

问题描述： 加粗样式从塔顶往下走，如何走过的步数最大

问题分析：

1. 数塔游戏（5层）
2. 从塔顶到塔底，走过的值最大
3. 从第一层开始，往左走还是往右走，变化两个4层他的问题，因此改问题存在子问题重叠性质
4. 由于该问题要求走过的值最大，因此，该问题存在要求最优解，因此符合动态规划用法
5. 递归求解过程：

   1. 塔数据用二维数组存储d[5][5],规划表格用maxD[5][5]存储(用来存储子问题的解),该结构是下三角结构

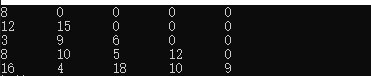
   2. 划分子问题：第1层走左还是走右取决去第2层哪个值最大，max(2)，第二层变化两个4层他的问题

   3. 递推公式：第一层的最优解有d[0][0] + max{maxD[1][0], maxD[1][1]}，第i层的最优解为d[i][j] = amx{maxD[i+1][j], maxD[i+1][j+1]}， 最后一层的最优解是自己，级maxD[n-1][j] = d[n-1][j]

   4. 填表,表的最顶部的就是最优解

算法实现

#include<iostream>
using namespace std; 

int max(int a, int b) {
	return a > b ? a : b;
}

int main() {
	int n = 5;
	int d[5][5] = {{8, 0}, {12, 15, 0}, {3, 9, 6, 0}, {8, 10, 5, 12, 0}, {16, 4, 18, 10, 9}};
	int maxD[5][5] = {{0}, {0}, {0}, {0}, {16, 4, 18, 10, 9}};
	// 先填写最后一层
	for (int i = n-2; i>=0; i--) {
		for (int j = 0; j <= i; j++) {
			maxD[i][j] = d[i][j] + max(maxD[i+1][j], maxD[i+1][j+1]);
		}
	}
	// 输出初始值 
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cout<<d[i][j]<<"\t";
		}
		cout<<endl;
	}
	cout<<"初始"<<endl; 
	// 输出结果 
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cout<<maxD[i][j]<<"\t";
		}
		cout<<endl;
	}
	return 0;	
}

结果