前言
本文分析卡尔曼滤波和扩展卡尔曼滤波,包括:思路流程、计算公式、简单案例等。滤波算法,在很多场景都有应用,感觉理解其思路和计算过程比较重要。
目录
一、卡尔曼滤波
卡尔曼滤波思想由 kalman于 1960 年提出,该方法:
假设状态噪声与观测噪声符合高斯分布;
通过观测数据 对 状态量 进行最优估计。
其实质是计算最大后验概率问题,只能应用于线性系统。
1.1 KF计算公式
卡尔曼滤波法的核心问题是:如何建立滤波所需的状态方程和观测方程。在实际工作过程中,卡尔曼滤波法将为系统提供最优估计,其前提是系统应具备线性模型,使用卡尔曼滤波法可以简化计算量,并且节数据存储。
在定义系统的 状态方程 和 观测方程 分别如下:
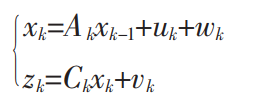
第一条公式:定义 k-1 时刻的状态为?,其对应的协方差为
。k时刻(当前时刻)的状态为
;思路:先用上一时刻的状态,来预估当前时刻的状态
。?
第二条公式:定义为当前时刻的观测值。思路:通过预估当前时刻的状态
?和观测变量
,来计算观察值
1.2 KF迭代过程
?(1)预测:

?(2)更新:
首先更新卡尔曼增益 K:
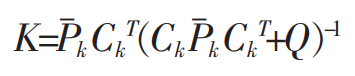
?然后基于卡尔曼增益 K再更新?更新后验概率分布(即:状态值、协方差)
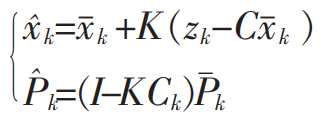
1.3 KF使用说明
卡尔曼滤波仅适用于线性高斯系统, 目前大多数情况下机器人所涉及的状态估计是非线性的, 卡尔曼滤波的结果并不可靠。
针对卡尔曼滤波的缺陷,学者们提出了许多改进方法, 如扩展卡尔曼滤波(EKF)、无损卡尔曼滤波(UKF)、压缩扩展 卡尔曼滤波(CEKF)……。
二、卡尔曼滤波案例——多目标跟踪
多目标跟踪算法的经典算法DeepSort,它是一个两阶段的算法,达到实时跟踪效果,曾被应用于工业开发。
核心思想:使用递归的卡尔曼滤波和逐帧的匈牙利数据关联。
?假定跟踪场景是定义在 8 维状态空间(u, v, γ, h, ?, ?, γ?, ?)中, 边框中心(u, v),宽高比 γ,高度 h 和和它们各自在图像坐标系中的速度。
这里依旧使用的是匀速运动模型,并把(u,v,γ,h)作为对象状态的直接观测量。

在目标跟踪中,需要估计目标的以下两个状态:
?均值(Mean):包含目标的位置和速度信息,由 8 维向量(u, v, γ, h, ?, ?, γ?, ?)表示,其中每个速度值初始化为 0。均值 Mean 可以通过观测矩阵 H 投影到测量空间输出(u,v,γ,h)。
?协方差(Covariance):表示估计状态的不确定性,由 8x8 的对角矩阵表示,矩阵中数字越大则表明不确定性越大。
2.1?卡尔曼滤波器——预测阶段
?step1:首先利用上一时刻 k-1 的后验估计值,通过状态转移矩阵 F 变换,得到当前时刻 k 的先验估计状态
![]() ?
?
其中,状态转移矩阵 F如下:
 ?
?
??step2:然后使用上一时刻 k-1 的后验估计协方差来计算当前时刻 k 的先验估计协方差
![]() ?
?
通过上一时刻的后验估计均值和方差 估计?当前时刻的先验估计均值x和协方差P
实现代码如下:
def predict(self, mean, covariance):
# mean, covariance 相当于上一时刻的后验估计均值和协方差
std_pos = [
self._std_weight_position * mean[3],
self._std_weight_position * mean[3],
1e-2,
self._std_weight_position * mean[3]]
std_vel = [
self._std_weight_velocity * mean[3],
self._std_weight_velocity * mean[3],
1e-5,
self._std_weight_velocity * mean[3]]
# 初始化噪声矩阵 Q
motion_cov = np.diag(np.square(np.r_[std_pos, std_vel]))
# x' = Fx
mean = np.dot(self._motion_mat, mean)
# P' = FPF^T + Q
covariance = np.linalg.multi_dot((
self._motion_mat, covariance, self._motion_mat.T)) + motion_cov
# 返回当前时刻的先验估计均值 x 和协方差 P
return mean, covariance2.2?卡尔曼滤波器——更新阶段
- step1:首先利用先验估计协方差矩阵 P 和观测矩阵 H 以及测量状态协方差矩阵 R 计算出卡尔曼增益矩阵 K
![]() ?
?
- step2:然后将卡尔曼滤波器的先验估计值 x 通过观测矩阵 H 投影到测量空间,并计算出与测量值 z 的残差 y
![]() ?
?
 ?
?
- step3:将卡尔曼滤波器的预测值和测量值按照卡尔曼增益的比例相融合,得到后验估计值 x
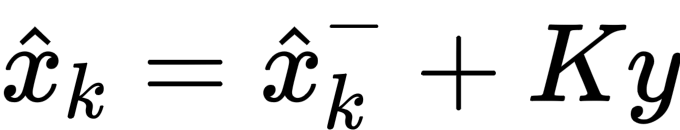 ?
?
- step4:计算出卡尔曼滤波器的后验估计协方差
![]() ?
?
?卡尔曼滤波器更新阶段,代码实现:
def update(self, mean, covariance, measurement):
# 将先验估计的均值和协方差映射到检测空间,得到 Hx' 和 HP'
projected_mean, projected_cov = self.project(mean, covariance)
chol_factor, lower = scipy.linalg.cho_factor(
projected_cov, lower=True, check_finite=False)
# 计算卡尔曼增益 K
kalman_gain = scipy.linalg.cho_solve(
(chol_factor, lower), np.dot(covariance, self._update_mat.T).T,
check_finite=False).T
# y = z - Hx'
innovation = measurement - projected_mean
# x = x' + Ky
new_mean = mean + np.dot(innovation, kalman_gain.T)
# P = (I - KH)P'
new_covariance = covariance - np.linalg.multi_dot((
kalman_gain, projected_cov, kalman_gain.T))
# 返回当前时刻的后验估计均值 x 和协方差 P
return new_mean, new_covariance总结一下:
?在目标跟踪中,需要估计目标的以下两个状态:
?均值(Mean):包含目标的位置和速度信息,由 8 维向量(u, v, γ, h, ?, ?, γ?, ?)表示,其中每个速度值初始化为 0。均值 Mean 可以通过观测矩阵 H 投影到测量空间输出(u,v,γ,h)。
?协方差(Covariance):表示估计状态的不确定性,由 8x8 的对角矩阵表示,矩阵中数字越大则表明不确定性越大。
predict 阶段和 update 阶段都是为了计算出卡尔曼滤波的估计均值 x?和协方差 P,不同的是前者是基于上一历史状态做出的先验估计,而后者则是融合了测量值信息并作出校正的后验估计。
详细参考:多目标跟踪算法 | DeepSort_一颗小树x的博客-CSDN博客_deepsort
三、扩展卡尔曼滤波 EKF
扩展卡尔曼滤波可以通过泰勒展开来解决非线性情况下的问题。
3.1??EKF计算公式

?其中 是展开后得到的一阶偏导项。 在展开过程中省略了次数较高的项,将状态估计方程转化为 近似的线性化方程。
是展开后得到的一阶偏导项。 在展开过程中省略了次数较高的项,将状态估计方程转化为 近似的线性化方程。
?3.2 EKF迭代过程
迭代过程与卡尔曼滤波大致相似,?
?(1)预测:
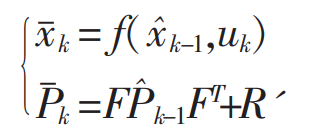
?(2)更新:
首先更新卡尔曼增益 K:
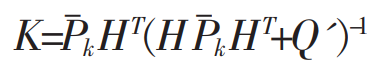
?然后基于卡尔曼增益 K再更新?更新后验概率分布(即:状态值、协方差)
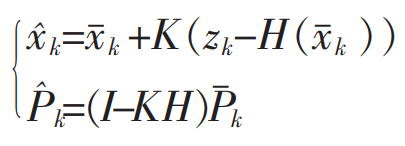
其中 R'与 Q' 为线性化后状态方程对应的新的协方差。
1.3 EKF使用说明
扩展卡尔曼滤波可以在非线性的场景下工作。但是,它在计算的时候忽略了展开式的高次项,因此估计会有误差,有可能会导致滤波器发散。
几种滤波器的对比说明
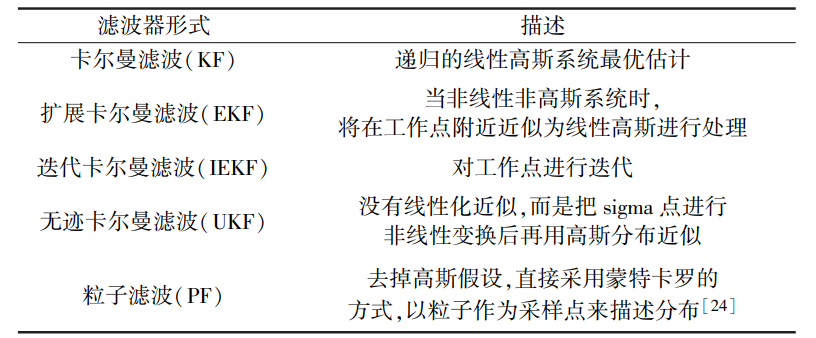
本文直供大家参考学习,谢谢!
参考文献:
[1]?李庆玲,许茂洲,张慧祥. SLAM 后端优化原理研究[J]. 技术设计与试验应用,2020.
[2]?危双丰,庞 帆,刘振彬, 师现杰. 基于激光雷达的同时定位与地图构建方法综述[J]. 计算机应用研究,2020.