Code For 1

题意：给定一个数n，如果这个数大于1，把这个数拆分成3个数在这里插入图片描述
成为一个序列，对于序列中大于1 的数进行以上操作，直到序列中只有0和1，问区间【l，r】内有多少个1

n的数据范围不超过 $2^{50}$ ,int数据范围是 $2^{32}$

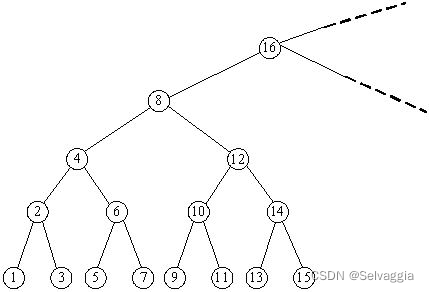
模拟二叉树中序遍历特征的做法

1125899906842623 1 100001
这个魔鬼样例，超出题目说的范围了，恰好 $2^{50}$

这张图片好看，节点内的数值是中序遍历的序号
在这里插入图片描述

#include <iostream>
#include <algorithm>
#include <math.h>
#include <vector>
#define int long long 
using namespace std;

signed main(){
	int n,l,r;//注意了n是longlong型 
	cin>>n>>l>>r;
	if(n==0||n==1){
		cout<<n;
		return 0;
	} 
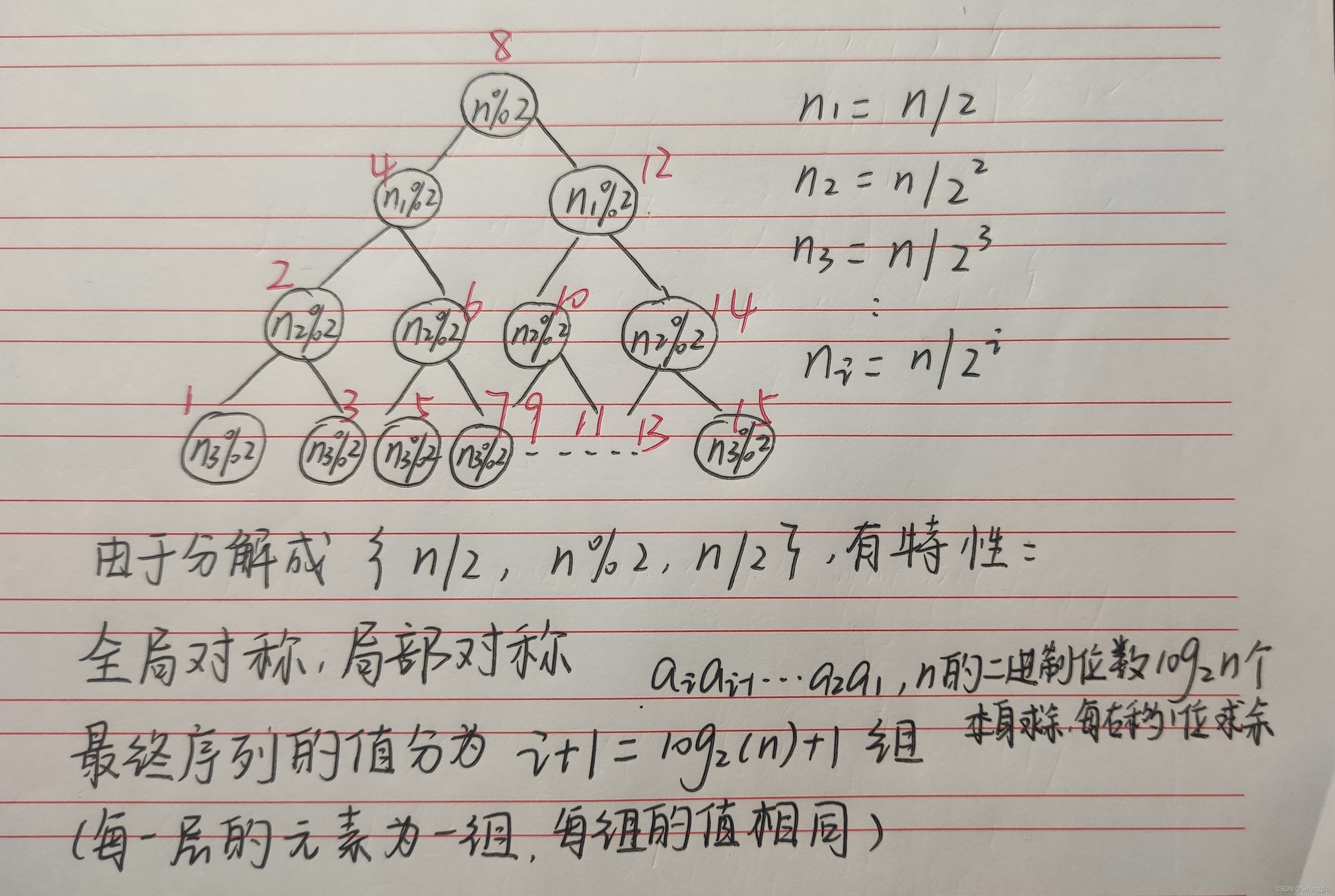
	int cnt=log2(n)+1;//n在二叉树的层数，每层的所有元素相等
//	本身占一层，能连除 log2(n)次 

	vector<int> v;
	v.clear(); 
	while(n){
		v.push_back(n%2);//由高层到低层存入每一层的值 
		n>>=1;
	}
//	cout<<cnt<<" "<<v.size()<<endl;// 51 50??? 
//1125899906842623 1 100001
//这个样例，心力交瘁,不转置过不了 

	reverse(v.begin(),v.end());
	//v数组存入了cnt个值，转置一下恰好，下标+1对应了层数
	//当然了不转置也可以，可以通过元素对应的层数与最高层的差值查到该层的值
//	res+=v[cnt-ceng]; 
	int res=0;
	for(int i=l;i<=r;i++){//l，r对应着中序排列的序号 
		int ceng=log2(i&(-i))+1;//中序遍历的第i个数所在的层数 
		if(v[ceng-1]==1)res++;//减一是因为数组下标从0开始
//			res+=v[cnt-ceng];
	} 
	cout<<res;
    return 0;
}

好的，都过不去。。。
为什么我会突发奇想添油加醋先搞个排序还撞对了，大佬们几年前的题解现在交上去都过不去那个魔鬼样例，可能是后面加强了数据（加了个超出数据范围的样例？）

#include <iostream>
#include <algorithm>
#include <math.h>
#include <map>
#define int long long 
using namespace std;

signed main(){
	int n,l,r;//注意了n是longlong型 
	cin>>n>>l>>r;
	if(n==0||n==1){
		cout<<n;
		return 0;
	} 
	int cnt=log2(n);
	cnt=pow(2,cnt+1);
	cnt/=2;
	map<int,int> mp;
	mp.clear(); 
	while(cnt){
//		cout<<cnt<<endl;
		mp.insert({cnt,n%2});
		cnt>>=1;
		n>>=1;
	}

	int res=0;
	for(int i=l;i<=r;i++){//l，r对应着中序排列的序号 
		int ceng=log2(i&(-i));
		int x=pow(2,ceng); 
//		cout<<ceng<<" "<<x<<" "<<mp[x]<<endl;
		if(mp[x]==1)res++;//减一是因为数组下标从0开始
	} 
	cout<<res;
    return 0;
}

参考思路

参考做法，要动手画二叉树
 这位博主也是，转置了才能AC，ｗｈｙ？

递归分治

8 下面有3层，x和自x以下共有4层，每层的数量呈等比数列
1+2+4+8
根据等比数列，2^n -1,首项为1，共有n项
可以计算出，最终序列的长度
或者直接len=1，len=len*2+1,n/=2;

递归自然就是在1~len范围内，还是可以构想一颗二叉树，递归的过程是
得到左右两颗子树，分别计算出左右两棵子树中的1的个数

#include <iostream>
#include <algorithm>
#include <math.h>
#define int long long 
using namespace std;
int n,lx,rx;//注意了n是longlong型 
int solve(int x,int l,int r){//根节点数值，所有节点下标范围 
	if(r<lx||l>rx)return 0;
	if(x<2){
		if(l>=lx&&r<=rx)return x;//x是0或者1，不能再分了
		else return 0; 
	}
	int half=(l+r)>>1;//只能根据节点数确定子树中节点范围，x只是个数值，不易求下标 
	//左右子树各分走一半节点 
	return solve(x/2,l,half-1)+solve(x%2,half,half)+solve(x/2,half+1,r); 
}
signed main(){

	cin>>n>>lx>>rx;
	if(n==0||n==1){
		cout<<n;
		return 0;
	} 
	int x=n,len=1;
	while(x!=1){
		len=len*2+1;
		x/=2;
	}
//	len=pow(2,log2(x)+1)-1;//等比数列公式 
	cout<<solve(n,1,len);//根节点，以该根节点为子树的元素下标范围 
    return 0;
}