矩阵连乘问题
计算A1A2…An的最小代价方法(最小时间复杂度,乘法次数),返回最优值和最优解。若A是pq矩阵,B是qr矩阵,则AB的代价是O(pqr)


void MatrixChain(int *p,int n,int **m,int **s)
{ for (int i = 1; i <= n; i++) m[i][i] = 0;//对角线值初始化为0
for (int r = 2; r <= n; r++)//一共有r个矩阵相乘
for (int i = 1; i <= n - r+1; i++)
{
int j=i+r-1;//Ai*Ai+1*....*Aj(共有r个矩阵相乘,j-i+1=r)
m[i][j] = m[i][i]+m[i+1][j]+ p[i-1]*p[i]*p[j];//k=i的情况
s[i][j] = i;
for (int k = i+1; k < j; k++)//依次列举k=i+1的情况
{
int t = m[i][k] + m[k+1][j] + p[i-1]*p[k]*p[j];
if (t < m[i][j]) { m[i][j] = t; s[i][j] = k;}
}
}
}
#include "stdio.h"
#include "math.h"
#include <conio.h>
void MatrixChain( long int *p, long int n,long int m[100][100],long int s[100][100])
{ long int i,j,r,k,t;
for (i=1; i<=n; i++) m[i][i]=0;
for (r=2; r<=n; r++)
for (i=1; i<=n-r+1; i++)
{ j=i+r-1;
m[i][j]=m[i][i]+m[i+1][j]+p[i-1]*p[i]*p[j];
s[i][j]=i;
for ( k=i+1; k<j; k++)
{ t=m[i][k]+m[k+1][j]+p[i-1]*p[k]*p[j];
if (t< m[i][j]) { m[i][j]=t; s[i][j]=k; }
} } }
void Traceback( long int i, long int j,long int s[100][100])
{
if (i==j) return;
Traceback(i,s[i][j],s);
Traceback(s[i][j]+1,j,s);
printf("%ld,%ld,%ld\n",i,j,s[i][j]);
}
int main()
{
long int p[100]; long int n; long int m[100][100],s[100][100];
n=6; p[0]=30; p[1]=35; p[2]=15; p[3]=5; p[4]=10; p[5]=20; p[6]=25;
MatrixChain( p, n, m,s);
printf("zuiyouzhi=%ld",m[1][6]);
printf("\ns[1][6]=%ld\n",s[1][6]);
Traceback( 1, n, s);
getch();}

最长公共子序列问题

1 设序列X={x1,x2,…,xm}和Y={y1,y2,…,yn}的最长公共子序列为Z={z1,z2,…,zk} ,则
(1)若xm=yn,则zk=xm=yn,且Zk-1是Xm-1和Yn-1的最长公共子序列。
(2)若xm≠yn且zk≠xm,则Z是Xm-1和Y的最长公共子序列。
(3)若xm≠yn且zk≠yn,则Z是X和Yn-1的最长公共子序列。
其中,Xm-1={x1,x2,…,xm-1}, Yn-1={y1,y2,…,yn-1} Zk-1={z1,z2,…,zk-1}
2 得出最优值的递归关系

3 自底向上计算最优值
例子:

#include <stdio.h>
#include <string.h>
#define MAXLEN 100
void LCSLength(char *x, char *y, int m, int n, int c[][MAXLEN], int b[][MAXLEN])
{
//
int i, j;
//初始化为0
for(i = 0; i <= m; i++) c[i][0] = 0;
for(j = 1; j <= n; j++) c[0][j] = 0;
//双层循环
for(i = 1; i<= m; i++)
for(j = 1; j <= n; j++)
{
if(x[i] == y[j])
{
c[i][j] = c[i-1][j-1] + 1;
b[i][j] = 1;//标记为左上角
}
else if(c[i-1][j] >= c[i][j-1])
{
c[i][j] = c[i-1][j];
b[i][j] = 2;//上
}
else
{
c[i][j] = c[i][j-1];
b[i][j] = 3;//左
}
}
}
void PrintLCS(int b[][MAXLEN], char *x, int i, int j)
{
if(i == 0 || j == 0) return;
if(b[i][j] == 1)
{
PrintLCS(b, x, i-1, j-1);
printf("%c ", x[i]);
}
else if(b[i][j] == 2)
PrintLCS(b, x, i-1, j);
else
PrintLCS(b, x, i, j-1);
}
int main(int argc, char **argv)
{
char x[MAXLEN] = {" ABCBDABPP"};
char y[MAXLEN] = {" BDCABAPQ"};
int b[MAXLEN][MAXLEN];
int c[MAXLEN][MAXLEN];
int m, n;
m = strlen(x);
n = strlen(y);
LCSLength(x, y, m, n, c, b);
PrintLCS(b, x, m, n);
return 0;
}
时间复杂性:计算最优值O(mn), 构造最优解O(m+n),总体O(mn)
空间复杂性:使用数组C和B,O(mn)
最大子段和问题

1简单算法
O(n3)
O(n2)
2 分冶策略 T(n)=O(nlogn)
int MaxSum(int *a, int left, int right)
{
int sum=0, leftsum, rightsum, center, s1=0, lefts=0, rights=0, s2=0;
if( left==right)//最小区间
if(a[left]>0) return a[left];
else return 0;
else
{
center=(left+right)/2;
leftsum=MaxSum(a,left,center);
rightsum=MaxSum(a,center+1, right);
for(i=center; i>=left; i--) //一个i值对应一个子段和
{
lefts=lefts+a[i];
if(lefts>s1) s1=lefts;//从center开始往回找到最大的和
}
for(i=center+1; i<=right; i++)
{
rights=rights+a[i];
if(rights>s2) s2=rights;//从center+1往后找到最大的和
}
sum=s1+s2;
if(sum<leftsum) sum=leftsum;
if(sum<rightsum) sum=rightsum;
}
return sum;
}
3 动态规划算法
子问题的界定:
前边界为1,后边界i,b[i]是A[1…i]中必须包含元素A[i]的向前连续延伸的最大字段和
递推方程:
b[i]=max{b[i-1]+A[i], A[i]} i=2,…,n
b[1]=A[1] 若A[1]>0
b[1]=0 否则
最大子段和为:
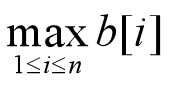
int MaxSum(int n, int *a, int *c, int *d)
{
int *b, sum; sum=0; b[0]=0;
for(i=1; i<=n; i++)
{ if(b[i-1]>0)//b[i]=max{b[i-1]+A[i], A[i]}
{ b[i]=b[i-1]+a[i]; c[i]=1;}//c[i]=1标记,b[i]=b[i-1]+A[i]
else {b[i]=a[i]; c[i]=0;}//b[i]=A[i]
if(b[i]>sum) {sum=b[i]; (*d)=i;}
}
return sum;
}
void output(int *c, int d)
{
int i=d;
do
{ if(i==d)
printf("=%d",a[i]);
else
printf("+%d",a[i]);
}while(c[i--]==1);//如果c[i]==1 就往前走,来判断第一个数的下标,c[i]==0,就退出
}
凸多边形最优三角剖分
目前还理解
0-1背包问题

void Knapsack(int * v, int *w, int c, int n, int m[10][10])
{
int jMax,j,i;
jMax=(w[n]-1)<c?(w[n]-1):c; //jMax:列数
for ( j=0; j<=jMax; j++) m[n][j]=0;//最后一行全为0
for ( j=w[n]; j<=c; j++) m[n][j]=v[n];//将最后一行中,小于背包容量的全为赋值为选最后物品的价值
for( i=n-1; i>1; i--)
{
jMax=(w[i]-1)<c?(w[i]-1):c;
for ( j=0; j<=jMax; j++)//背包容量小于该行物品容量
m[i][j]=m[i+1][j];//不选
for ( j=w[i]; j<=c; j++)
m[i][j]=m[i+1][j]>(m[i+1][j-w[i]]+v[i])?m[i+1][j]:(m[i+1][j-w[i]]+v[i]);
}
m[1][c]=m[2][c];
if(c>=w[1])
m[1][c]=m[1][c]>(m[2][c-w[1]]+v[1])?m[1][c]:(m[2][c-w[1]]+v[1]);
}