94. 二叉树的中序遍历
给定一个二叉树的根节点 root ,返回 它的 中序 遍历 。
示例 1:
输入:root = [1,null,2,3]
输出:[1,3,2]
示例 2:
输入:root = []
输出:[]
示例 3:
输入:root = [1]
输出:[1]
递归非递归都是很统一的思路,要输出父母结点就必须先输出左孩子结点再输出父母结点再输出右孩子结点。每个结点都应该这样操作。
首先是简单的递归中序遍历,大体思路记录一下吧,先输出左孩子,再输出父节点,再输出右孩子。输出左孩子f也是先输出左孩子的左孩子,再输出这个f然后再输出f的右孩子,显然是个递归。就直接函数调用。
或者可以这样理解
class Solution {
public:
//存储结果
vector<int> result;
void mid(TreeNode* root)
{
//根不为空
if(root)
{
//遍历左子树
mid(root->left);
//输出根节点(对于第一个要输出的左节点,其实可以看成根节点,只不过是一个没有左右子树的根结点,希望可以帮助不太理解的理解下递归)
result.push_back(root->val);
//遍历右子树
mid(root->right)
}
}
vector<int> inorderTraversal(TreeNode* root) {
mid(root);
return result;
}
};
非递归的中序遍历,要借用栈,其实递归本身就是用栈实现的,思路和上面类似,我要输出父节点,就必须先输出左孩子。要输出这个左孩子,就必须输出它的左孩子。那就需要把父节点的左孩子压入栈,先处理左孩子的那个左孩子。后进先出,所以要用栈
class Solution {
public:
vector<int> inorderTraversal(TreeNode* root) {
//建立栈存储结点
stack<TreeNode*> st;
//存储结果
vector<int> result;
//auto自动推断类型,建立变量存储root
auto q=root;
//这里的q主要是针对根节点的进入,如果根结点为null不会进入
//当栈内的元素弹完了,树也就遍历完了
while(q||!st.empty())
{
//将左子树全部压入栈
while(q)
{
st.push(q);
q=q->left;
}
//当没有左子树时,栈上的top点应该是最先输出的,从栈内弹出它并把这个叶子的值放入result数组中
auto node=st.top();
st.pop();
result.push_back(node->val);
//处理刚才那个点的右子树
q=node->right;
}
return result;
}
};
101. 对称二叉树
给你一个二叉树的根节点 root , 检查它是否轴对称。
示例 1:
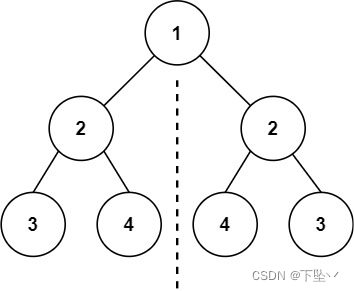
输入:root = [1,2,2,3,4,4,3]
输出:true
提示:
树中节点数目在范围 [1, 1000] 内
-100 <= Node.val <= 100
首先考虑递归的思路:
对称二叉树上面的图应该很容易了解了,两个结点,一个结点的左子树等于另一个结点的右子树,另一个结点的右子树又等于这个结点的左子树。对每一个结点都应当是这样判断的,可以把从树的根拆开,这样就可以对两棵树进行比较了
class Solution {
public:
bool is(TreeNode* root1,TreeNode* root2)
{
//当两个结点都不存在时返回true
if(!root1&&!root2)
{
return true;
}
//只有一个结点不存在时返回false
if(!root1||!root2)
{
return false;
}
//比较两个结点的值,并且递归
return root1->val==root2->val&&is(root1->left,root2->right)&&is(root1->right,root2->left);
}
bool isSymmetric(TreeNode* root) {
return is(root,root);
}
};
非递归的思路:
还是从根结点拆开为两个树,因为我们从头开始判断,遇到不相等的就结束,所以借用队列这一工具,将a树的左节点与b树的右节点比较,将a树的右节点再与b树的左节点比较。同时每次结点比较完毕,就应该把他对应的左右结点压入队列,以免丢失剩下的结点。
class Solution {
public:
bool isSymmetric(TreeNode* root) {
queue<TreeNode*> qu;
//拆为两棵树
qu.push(root);
qu.push(root);
while(!qu.empty())
{
//从头连续取出两个结点
auto a=qu.front();
qu.pop();
auto b=qu.front();
qu.pop();
//均为空也是相等的,但是没有左右子树可以插入
if(!a&&!b)continue;
//一方为空或者值不相等则返回不相等
if(!a||!b) return false;
if(a->val!=b->val) return false;
//左右,右左插入(每次插入的两个值应该时相等的)
qu.push(a->left);
qu.push(b->right);
qu.push(a->right);
qu.push(b->left);
}
return true;
}
};
100. 相同的树
给你两棵二叉树的根节点 p 和 q ,编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
示例 1:
输入:p = [1,2,3], q = [1,2,3]
输出:true
示例 2:
输入:p = [1,2], q = [1,null,2]
输出:false
递归思路:
对于每个结点,如果都为空则相等,其中一个为空则不相等,(这两个必须先处理,不然处理数可能存在空指针,会报错)数不同不相等,相同的话再判断它们的左孩子和右孩子。这样一想,循环体就有了
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
//先判断节点的存在情况
if(!p&&!q)
{
return true;
}
if(!p||!q)
{
return false;
}
if(p->val!=q->val)
{
return false;
}
//判断值和左右子树
return p->val==q->val&&isSameTree(p->left,q->left)&&isSameTree(p->right,q->right);
}
};
非递归思路
因为一遇到不同的就终止,所以使用队列,其实这个题和上题的思路很像,只不过不是左对右,右对左压入了,而是左对左,右对右的压入比较
class Solution {
public:
bool isSameTree(TreeNode* p, TreeNode* q) {
queue<TreeNode*> qu;
qu.push(p);
qu.push(q);
while(!qu.empty())
{
//连续取两个节点
auto a=qu.front();
qu.pop();
auto b=qu.front();
qu.pop();
//均不存在是相等的,但是无插入操作
if(!a&&!b)continue;
//单个存在或值不相等,返回不相等
if(!a||!b)return false;
if(a->val!=b->val)return false;
//连续插入左左,右右
qu.push(a->left);
qu.push(b->left);
qu.push(a->right);
qu.push(b->right);
}
return true;
}
};
98. 验证二叉搜索树
给你一个二叉树的根节点 root ,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树定义如下:
节点的左子树只包含 小于 当前节点的数。
节点的右子树只包含 大于 当前节点的数。
所有左子树和右子树自身必须也是二叉搜索树。
示例 1:
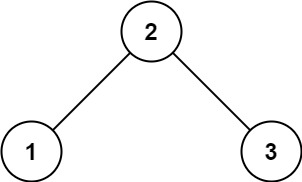
输入:root = [2,1,3]
输出:true
思路:
递归思路
我们先把注意力集中在单个节点的判断上,即它的左孩子应该小于父节点,右孩子应该大于父节点。事情的特殊点在于父节点R左孩子R1的右孩子r1和右孩子R2的左孩子r2。r1应该在大于R1的同时小于R,r2应该在小于R2的同时大于R。因此在处理时应该把R的值传下来用作判断R1和R2的孩子的限制。给左子树则作为上界,右子树作为下界。可以保证左右两边的子树合理。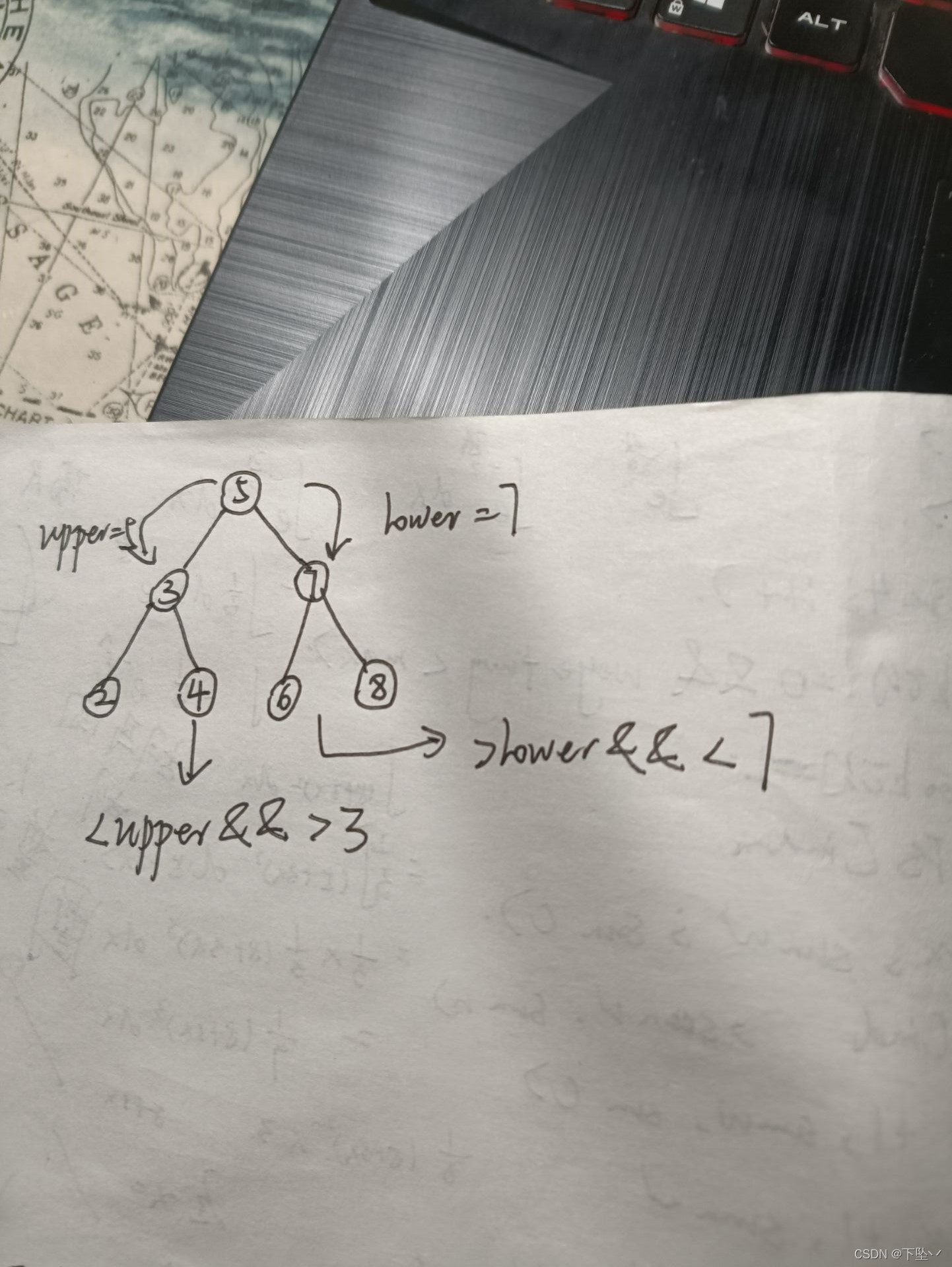
class Solution {
public:
bool is(TreeNode* root,long long int upper,long long int lower)
{
//节点为空和值不相等的状况
if(!root)
{
return true;
}
if(root->val>=upper||root->val<=lower)
{
return false;
}
//继续比对下一层
return is(root->left,root->val,lower)&&is(root->right,upper,root->val);
}
bool isValidBST(TreeNode* root) {
//upper和lower初值分别设最大和最小,因为范围在正负2的31次方
return is(root,LONG_MAX,LONG_MIN);
}
};
中序遍历排列
对二叉搜索树进行中序遍历,得到的结果必然是一个递增序列。例如上图,得到的中序遍历应当是2345678。因此中序遍历二叉树,只要发现不是递增的点就不是二叉搜索树
写完之后看了官方的版本,我这个版本其实不太好,其实不需要使用队列来存储节点的值,直接保存上一个节点的值进行比较就好了
class Solution {
public:
bool isValidBST(TreeNode* root) {
//中序遍历的工具栈
stack<TreeNode*> qu;
//借由存储节点的值
queue<int> adjust;
auto q=root;
//第一次不需要比较,执行一次adjust.pop()之后才开始比较
bool key =false;
while(q||!qu.empty())
{
while(q)
{
qu.push(q);
q=q->left;
}
auto node=qu.top();
qu.pop();
adjust.push(node->val);
if(key)
{
//弹出队列的第一个值,和此时队列的头比较
auto a=adjust.front();
adjust.pop();
if(a>=adjust.front())
{
return false;
}
}
q=node->right;
key=true;
}
return true;
}
};
上一下官方的代码做参考
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> stack;
long long inorder = (long long)INT_MIN - 1;
while (!stack.empty() || root != nullptr) {
while (root != nullptr) {
stack.push(root);
root = root -> left;
}
root = stack.top();
stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root -> val <= inorder) {
return false;
}
inorder = root -> val;
root = root -> right;
}
return true;
}
};
作者:LeetCode-Solution
链接:https://leetcode-cn.com/problems/validate-binary-search-tree/solution/yan-zheng-er-cha-sou-suo-shu-by-leetcode-solution/
来源:力扣(LeetCode)
著作权归作者所有。商业转载请联系作者获得授权,非商业转载请注明出处。
剑指 Offer 33. 二叉搜索树的后序遍历序列
输入一个整数数组,判断该数组是不是某二叉搜索树的后序遍历结果。如果是则返回 true,否则返回 false。假设输入的数组的任意两个数字都互不相同。
参考以下这颗二叉搜索树:
5
/
2 6
/
1 3
示例 1:
输入: [1,6,3,2,5]
输出: false
示例 2:
输入: [1,3,2,6,5]
输出: true
递归思路
二叉搜索树上方已经提到过,左子树全部小于根,右子树全部大于根。而后续遍历最末尾一个元素一定是根。因此将数组和根比较。前面小于根的元素一定是左子树,那么除根之外的元素一定是右子树,我们只用判断剩下的这些元素是不是全部大于根。若不是则返回false,是则对左子树和右子树再进行上面的算法比较,直到全部比较完为止
才发现我的记忆出了错乱,之前判断函数全用的adjust,应该用judge才对。而且这次代码中名字又写错了。。。第一个手快打错后面提示就跟着错
class Solution {
public:
bool judeg(vector<int>& postorder,int start,int end)
{
//表明比较完了
if(start>=end)
{
return true;
}
//记录根的值,记不记其实无所谓
int key=postorder[end];
//递归还要用到start,所以要建变量
int i=start;
//这都是左子树。循环结束时i在左子树后一位
while(postorder[i]<key)
{
i++;
}
//这都是右子树,同上
int m=i;
while(postorder[m]>key)
{
m++;
}
//中途右不大于根的,说明不是二叉搜索树
if(m!=end)
{
return false;
}
//继续判断上方的左右子树是不是二叉搜索树
return m==end&&judeg(postorder,start,i-1)&&judeg(postorder,i,end-1);
}
bool verifyPostorder(vector<int>& postorder) {
return judeg(postorder,0,postorder.size()-1);
}
};
单调栈
大体的思路就时倒历后序遍历,(后序遍历左右根,倒历就是根右左)借由栈。初始设置根为无穷大,后序遍历的时候,根一定出现在左子树的后面,因此倒叙时,根应该比左子树先出现,把根压入栈中,在遇到左子树之前,出现的一定是递增序列(如果右子树为右子树单链表则会出现递增序列)。因此把栈弹到最后一个大于左子树结点的一定是左子树的根。这个根的右子树一定都处理完了,接下来的就都是它的左子树或者这个根的父节点左子树,这些左子树都应当比根小,将这些都顺序处理掉,直到遇到一个新的递增序列,这个递增序列一定是一个根的右子树,再次找到这个右子树所连的根…
感觉其实也讲不太清楚,弄一个案例帮助理解吧
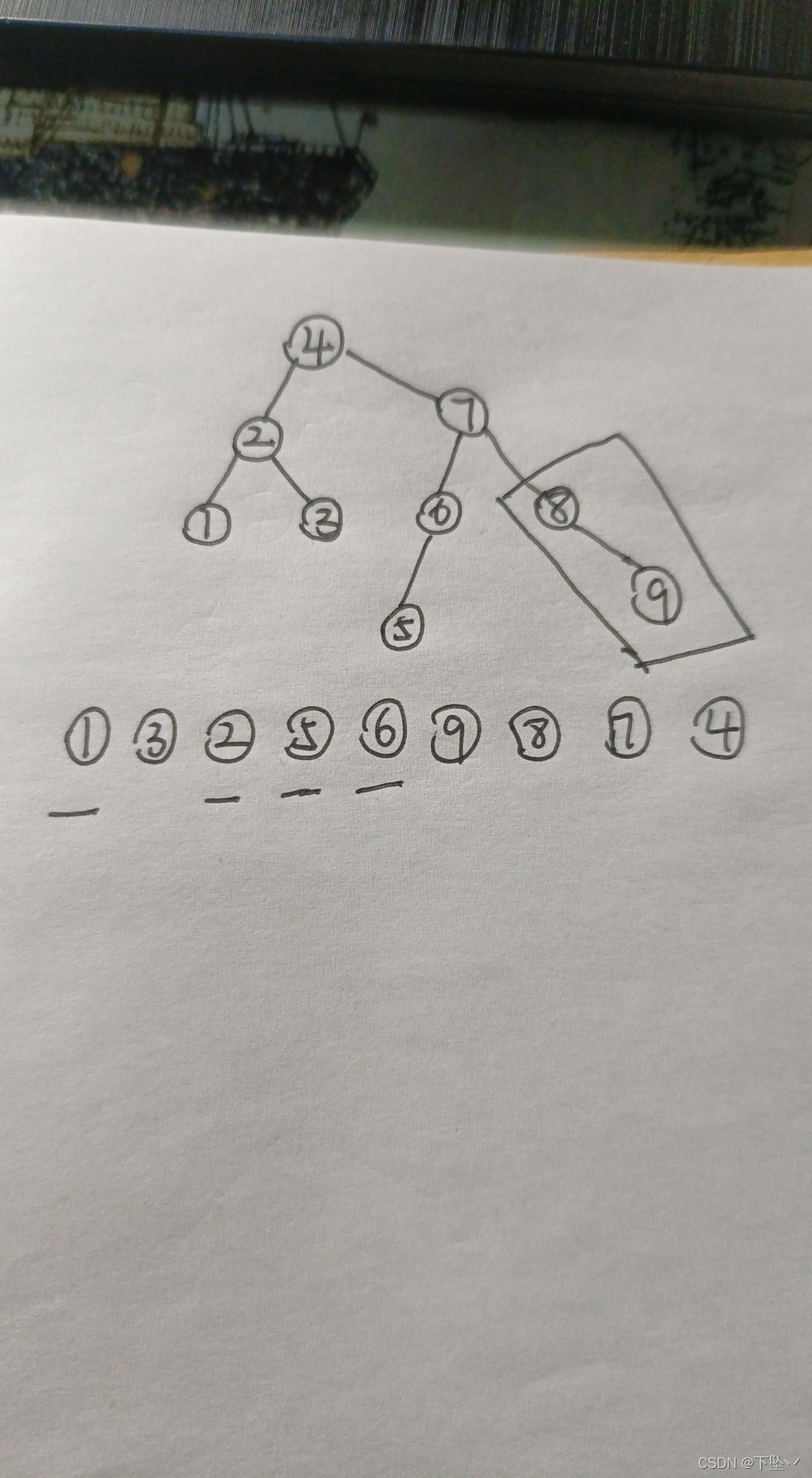
画横线的都是左子树,可以看出所有的左子树都是小于根的,一开始令根等于无穷大,目的就是把最开始那一段右子树给拆掉
class Solution {
public:
bool verifyPostorder(vector<int>& postorder) {
stack<int> st;
int root=INT_MAX;;
for(int i=postorder.size()-1;i>=0;i--)
{
if(postorder[i]>root)
{
return false;
}
while(!st.empty()&&postorder[i]<st.top())
{
root=st.top();
st.pop();
}
st.push(postorder[i]);
}
return true;
}
};