一.归并排序

1.1归并排序引入

对于堆排序来说，因为用到了完全二叉树的深度是（log2n+1）的特性，所以效率就比较高，但是堆结构的设计比较复杂，现在我们想要可以直接利用完全二叉树来排序的方法，这个方法就是归并排序。

1.2归并排序的概念

归并排序是建立在归并操作上的一种有效的排序算法，归并排序对序列的元素进行逐层折半分组，然后从最小分组开始比较排序，合并成一个大的分组，逐层进行，最终所有的元素都是有序的。

1.3归并排序的原理

原理：假设初始序列含有n个记录，则可以看成是n个有序的子序列，每个子序列的长度为1，然后两两归并，得到n/2个长度为2或1的有序子数列，再两两归并，如此重复直到得到一个长度为n的有序序列为止。

1.4实例说明

(1).以4，5，8，1，7，2，6，3为例，排序过程：
在这里插入图片描述
(2).以84，9，18，19，48，12，90，84，8，12为例，排序过程：

这里的两两合并指的是两个组合并；
每组的数据单独看是有序的。

1.5具体步骤说明

以实例中的第一个为例：
在这里插入图片描述

序列逐层拆分如下：
在这里插入图片描述

然后从下往上逐层合并，首先对第一层序列1（只包含元素4）和序列2（只包含元素5）进行合并

创建一个大序列，序列长度为两个小序列长度之和，A、B指针分别指向两个小序列的第一个元素，C指向大序列的第一个元素
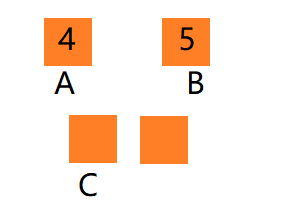
请添加图片描述
比较A、B指向的元素，4小于5，将4填入C指向的元素，C、A往右移一位

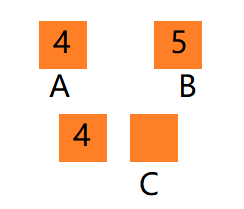
此时，序列1已经没有元素，将序列2的元素依次填入大序列中请添加图片描述
序列8和1，序列7和2，序列6和3，用同样的方式填入新的序列

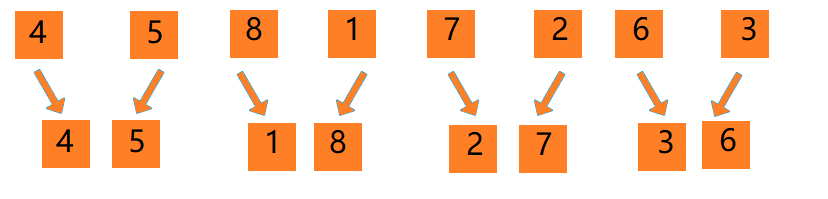
接着，以4、5为序列1，1、8为序列2，继续进行合并

创建一个序列长度为4的大序列，A指向序列1的第一个元素4，B指向序列2的第一个元素1，C指向大序列的第一个元素
在这里插入图片描述
4和1比较，4大于1，1填入C指向的元素，C、B往右移一位

4和8比较，4小于8，4填入C指向的元素，C、A往右移一位
请添加图片描述

5和8比较，5小于8，5填入C指向的元素，C、A往右移一位
请添加图片描述

自此，序列1已经没有元素，将序列2的元素依次填入大序列中
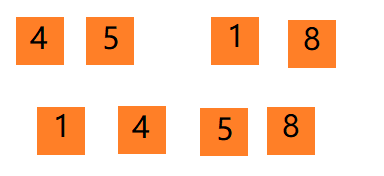
在这里插入图片描述
序列2、7和序列3、6以同样的方式合并成新的序列

最后，将序列1、4、5、8和序列2、3、6、7以同样的方式继续合并成新的序列

所有元素均已排好。

1.6代码实现

void MergeSort(int *arr, int len)
{
	for(int i=1; i<len; i*=2)// O（logn）
	{
		Merge(arr, len, i);
	}
	
}
//一次划分函数  核心函数  //返回基准值最终所在下标
int Partition(int *arr, int left, int right)
{
	//先讲arr数组里的[left， right]的第一个值 作为基准值
	int tmp = arr[left];

	while(left < right)
	{
		while(left<right && arr[right] > tmp)//左右边界没有相遇且当前右边的值大于基准值tmp
		right--;

		if(left < right)//如果此时，左右边界没有相遇，那就只能证明右边right找到了一个小于等于基准值tmp的值
		{
			arr[left] = arr[right];
		}
		else
		{
			break;
		}
		
		while(left<right && arr[left] <= tmp)//左右边界没有相遇且当前左边的值小于等于基准值tmp
		left++;

		if(left < right)//如果此时，左右边界没有相遇，那就只能证明左边left找到了一个大于基准值tmp的值
		{
			arr[right] = arr[left];
		}
		else
		{
			break;
		}
		
	}

	arr[left] = tmp;//此时 因为 left == right
	return left;//return right ok
}