开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 【力扣刷题】跟着labuladong刷力扣-----数据结构之二叉树 -> 正文阅读

[数据结构与算法]【力扣刷题】跟着labuladong刷力扣-----数据结构之二叉树

前言

刷题学框架,刷题学思想.跟着labuladong从二叉树开始刷力扣.
labuladong链接:labuladong代码小抄
刷题插件链接(来源labuladong公众号):
链接：https://pan.baidu.com/s/1glrZjyFCG4bXual3gzTvvw
提取码：un2k

一. 纲领篇

在刷题心得中,作者建议从二叉树开始建立思维,我也缺少递归思维,因此从二叉树开始刷题.

1. 解决二叉树问题的两种思维

是否可以通过遍历一遍二叉树得到答案? 如果可以,用一个traverse函数配合外部记录变量(如高度)来实现,这种是遍历的思维模式.
是否可以定义一个递归函数,每次递归都用子树的答案推导出原问题的答案? 如果可以,要给出递归函数的定义,并充分利用这个函数的返回值,这叫做分解问题的思维模式.

后面的刷题将从这两个思维模式进行分析,每到二叉树的题都会有1-2种解题思路.

2.理解二叉树的前中后序

抛开书本所讲,直接给出理解:前序位置就是刚进入一个节点的时候,后序位置就是即将离开一个节点的时候,中序位置就是左子树都遍历完,即将开始遍历右子树的时候,将代码写在不同位置,代码执行的时机就不同.

3.力扣104题:二叉树的最大深度(简单)

是否可以用遍历的思想解决: 可以!! 遍历每一个节点,并记录高度即可,最后返回最大高度.需要注意的是,力扣的提交系统处理全局存在一些规则:提交之后所用的测试用例共享全局变量和类变量,因此有些定义了全局变量的程序,在执行代码时是对的,但在提交时就有问题了.参考: https://leetcode-cn.com/circle/discuss/A2t74s/.回到本题,本题的代码如下:

var maxDepth = function(root) {
   // 最大的高度
   res = 0
   //记录高度
   depth = 0
   // 遍历二叉树
   traverse(root)
   return res
};

var traverse = function(root){
   // 遍历到叶子节点
   if(root === null){
       res = Math.max(res,depth)
       return 
   }
   // 进入节点时,高度加1
   depth++
   traverse(root.left)
   traverse(root.right)
   // 离开节点时,高度减1
   depth--
}

关于为什么离开节点时,高度要减1的问题,我觉得这样解释比较好,因为遍历到右子树后左子树的高度就不能要了,因此要减1.

是否可以用分解问题的思想解决:**也可以!!**因为大树的高度是由子树的高度加起来的,代码比较简单

// maxDepth定义为计算一棵树的高度
var maxDepth = function(root){
   if(root === null){
       return 0
   }
   // 计算左子树高度
   var leftDepth = maxDepth(root.left)
   // 计算右子树高度
   var rightDepth = maxDepth(root.right)
   // 当前最大的高度为左右的最高加1
   var res = Math.max(leftDepth,rightDepth) + 1
   return res
}

4.力扣543题:二叉树的直径(简单)

所谓二叉树的直径，就是左右子树的最大深度之和，那么直接的想法是对每个节点计算左右子树的最大高度，得出每个节点的直径，从而得出最大的那个直径。(这个没搞清楚~~)

var diameterOfBinaryTree = function(root) {
    // 最大直径
    maxDiameter = 0
    // 遍历树
    maxDepth(root)
    return maxDiameter
};

var maxDepth = function(root){
    if(root === null){
        return 0
    }
    // 遍历左右子树
    var maxleft = maxDepth(root.left)
    var maxright = maxDepth(root.right)
    // 比较左右子树之和与目前最大高度的值
    maxDiameter = Math.max(maxDiameter,maxleft+maxright)
    return Math.max(maxleft,maxright) + 1
}

5. 力扣144题:二叉树的前序遍历(简单)

本题可以直接用遍历的思想解决,直接前序遍历

var preorderTraversal = function(root) {
    arr = []
    traverse (root)
    return arr
};

var traverse  = function(root){
    if(root === null){
        return
    }
    arr.push(root.val)
    traverse (root.left)
    traverse (root.right)
}

二. 思路篇

1.力扣226题:翻转二叉树(简单)

遍历思路:遍历每个节点,交换它的左右节点

var invertTree = function(root) {
   reverse(root)
   return root
};

var reverse = function(root){
   if(root === null){
       return
   }
   var temp = new TreeNode()
   temp = root.left
   root.left = root.right
   root.right = temp
   reverse(root.left)
   reverse(root.right)
}

迭代思路:定义一个函数,它可以交换一个节点的左右子树.

// 功能定义:交换左右子树的位置
var invertTree = function(root) {
    if(root === null){
        return null
    }
    var Left,Right = new TreeNode()
    // 对整颗树的操作,交换左右子树
    Left = invertTree(root.left)
    Right = invertTree(root.right)
    // 对当前子树的操作左子树给右边,右子树给左边
    root.left = Right
    root.right = Left
    return root
};

2.力扣114题:二叉树展开为链表(中等)

给函数输入一个节点root,以root为根的二叉树就会被扯平为一条链表,首先将左右子树拉平,然后把左子树放到右子树的位置上,右子树向下移.

//  定义：将以root为根的数拉平为链表
var flatten = function(root) {
    if(root === null){
        return 
    }
    // 递归拉平左右子树
    flatten(root.left)
    flatten(root.right)

    // 后序位置
    // 左右子树已经被拉平成一条链表
    let Left = root.left
    let Right = root.right
    
    // 将左子树作为右子树
    root.left = null
    root.right = Left

    // 将右子树接在左子树后面
    while(root.right!=null){
        root = root.right
    }
    root.right = Right
    return root
};

3.力扣116题:填充每个节点的下一个右侧节点指针(中等)

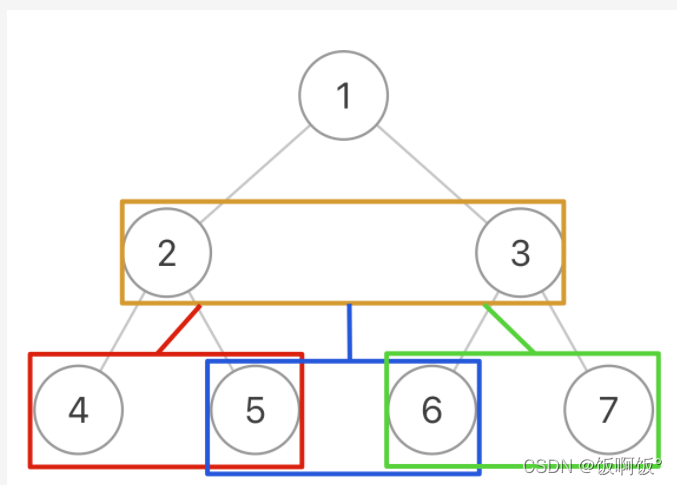
最初的思路一定是将左子树的right指向右子树,但是这样不能解决相邻的两个节点中,左边的右孩子要指向右边的左孩子的问题,两颗子树是分开的,因此labuladong大神给了一种思路,就是把二叉树的相邻节点抽象成一个三叉树节点,这样就把不是同一父节点的两个孩子关联起来了.(图片来源于labuladong)
在这里插入图片描述

var connect = function(root) {
    if(root === null) return null
    traverse(root.left,root.right)
    return root
};

var traverse = function(node1,node2){
    if(node1 === null || node2 === null){
        return
    }
    node1.next = node2
    traverse(node1.left,node1.right)
    traverse(node2.left,node2.right)
    traverse(node1.right,node2.left)
}

三. 构造篇

1. 力扣654题:最大二叉树(中等)

在这里插入图片描述
每一个二叉树节点都可以认为是一棵树的根节点,因此可以用分解的思路解决:选择最大的数作为根节点,然后将数组从最大数进行分界,递归构造左右子树.

var constructMaximumBinaryTree = function(nums) {
    return build(nums , 0 , nums.length - 1)
};
// 函数定义:用最大的数作根节点,左右两边成为左右子树
var build = function(nums,left,right){
    if(left > right){
        return null
    }
    var index = -1
    var maxVal = -Infinity
    // 最找最大值及其索引
    for(var i=left;i<=right;i++){
        if(maxVal < nums[i]){
            maxVal = nums[i]
            index = i
        }
    }
    // 构造根节点
    var root = new TreeNode(maxVal)
    // 构造左右子树
    root.left = build(nums,left,index-1)
    root.right = build(nums,index+1,right)
    return root
}

2. 力扣105题:从前序与中序遍历序列构造二叉树(中等)

在这里插入图片描述
二叉树的前序和中序遍历结果的特点如下:(图片来源:labuladong算法小抄)

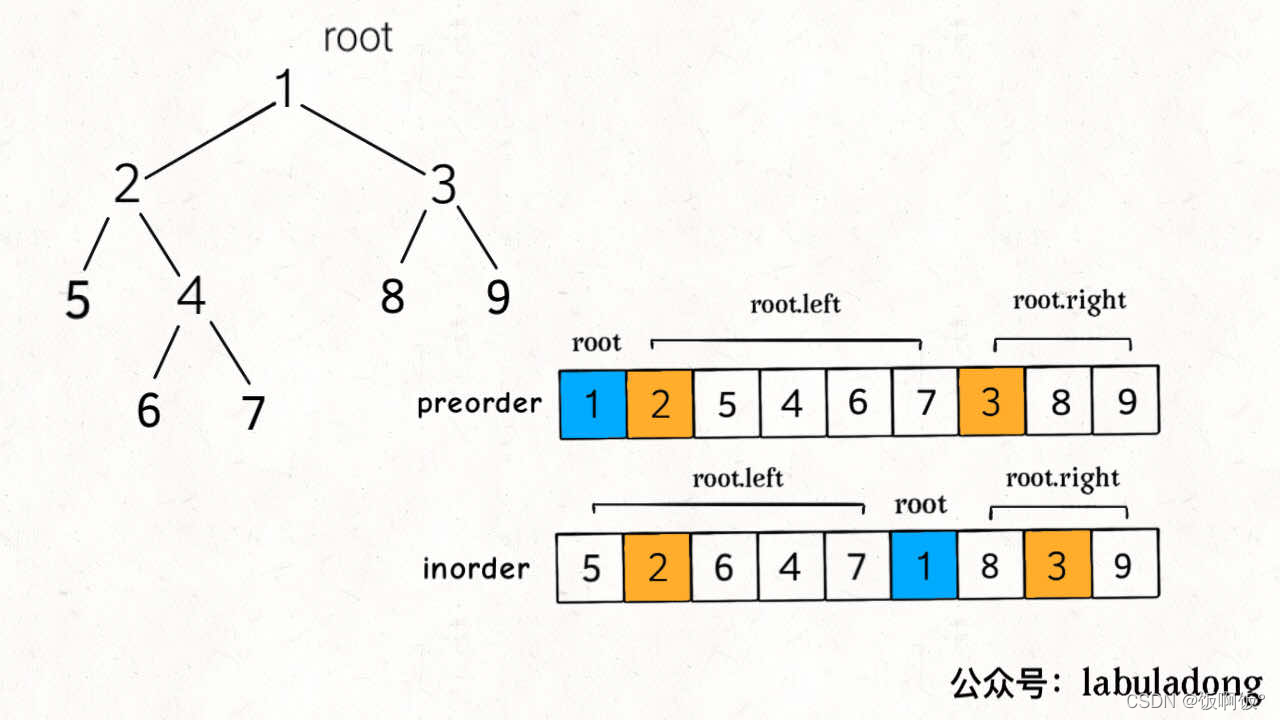
首先可以确定的是前序遍历的第一位就是整个树的根节点,在中序遍历中找到这个根节点,就可以把中序遍历分成左子树和右子树,再重新对左右子树做找根节点,拆分中序的做法,就可以得到整个二叉树.

var buildTree = function(preorder, inorder) {
    return build(preorder,0,preorder.length-1,inorder,0,inorder.length-1)
};
// 函数定义,给出前序遍历,以及起始边界,中序遍历,以及起始边界,得到一棵二叉树
var build = function(preorder,preStart,preEnd,inorder,inStart,inEnd){
    if(preStart > preEnd || inStart > inEnd){
        return null
    }
    // 取前序的第一个节点做根节点
    var root = new TreeNode(preorder[preStart])
    // 在中序中寻找根节点索引,就可以把中序分成左右两半了
    var index = inorder.indexOf(preorder[preStart])
    // 计算左子树大小,方便确定边界值
    var leftsize = index - inStart
    // 遍历生成左右子树
    root.left = build(preorder,preStart+1,preStart+leftsize,inorder,inStart,index-1)
    root.right = build(preorder,preStart+leftsize+1,preEnd,inorder,index+1,inEnd)
    return root
}

左子树参数解释
------preorder:前序遍历数据
------preStart+1:由于当前的第一位已经做了根节点,因此下一个根节点应该是preStart+1
------preStart+leftsize:此处应该是左子树数组结束的地方,就是左子树开始+左子树大小
------inorder:中序遍历数据
-----inStart:中序遍历最左边就是左子树的开始
-----index-1:左子树截至在根节点之前一位
右子树参数解释
------preorder:前序遍历数据
------preStart+leftsize+1:右子树第一位应该是左子树最后一位的下一位
------preEnd:右子树的最后一位就是数组的最后一位
------inorder:中序遍历数据
------index+1:中序遍历右子树就是根节点索引值的下一位
------inEnd:右子树截至在数组的最后一位

3. 力扣106题:从中序与后序遍历序列构造二叉树(中等)

在这里插入图片描述
思路与上题基本一直,只需修改递归的参数即可,不多余解释了,直接上代码

var buildTree = function(inorder, postorder) {
    return build(inorder,0,inorder.length-1,postorder,0,postorder.length-1)
};

var build = function(inorder,inStart,inEnd,postorder,posStart,posEnd){
    if(inStart > inEnd || posStart > posEnd){
        return null
    }
    var root = new TreeNode(postorder[posEnd])
    var index = inorder.indexOf(postorder[posEnd])
    var rightsize = inEnd - index
    root.left = build(inorder,inStart,index-1,postorder,posStart,posEnd-rightsize-1)
    root.right = build(inorder,index+1,inEnd,postorder,posEnd-rightsize,posEnd-1)
    return root
}

4. 力扣889题:根据前序和后序遍历构造二叉树(中等)

在这里插入图片描述
这里没有中序遍历了,因此就缺少了划分左右子树的标志,前序遍历是无法划分的,但是后序遍历可以通过前序的下一个值来划分左右子树,如图所示,(图片来源:labuladong算法小抄)(膜拜大神,写的实在是太好啦!!!)
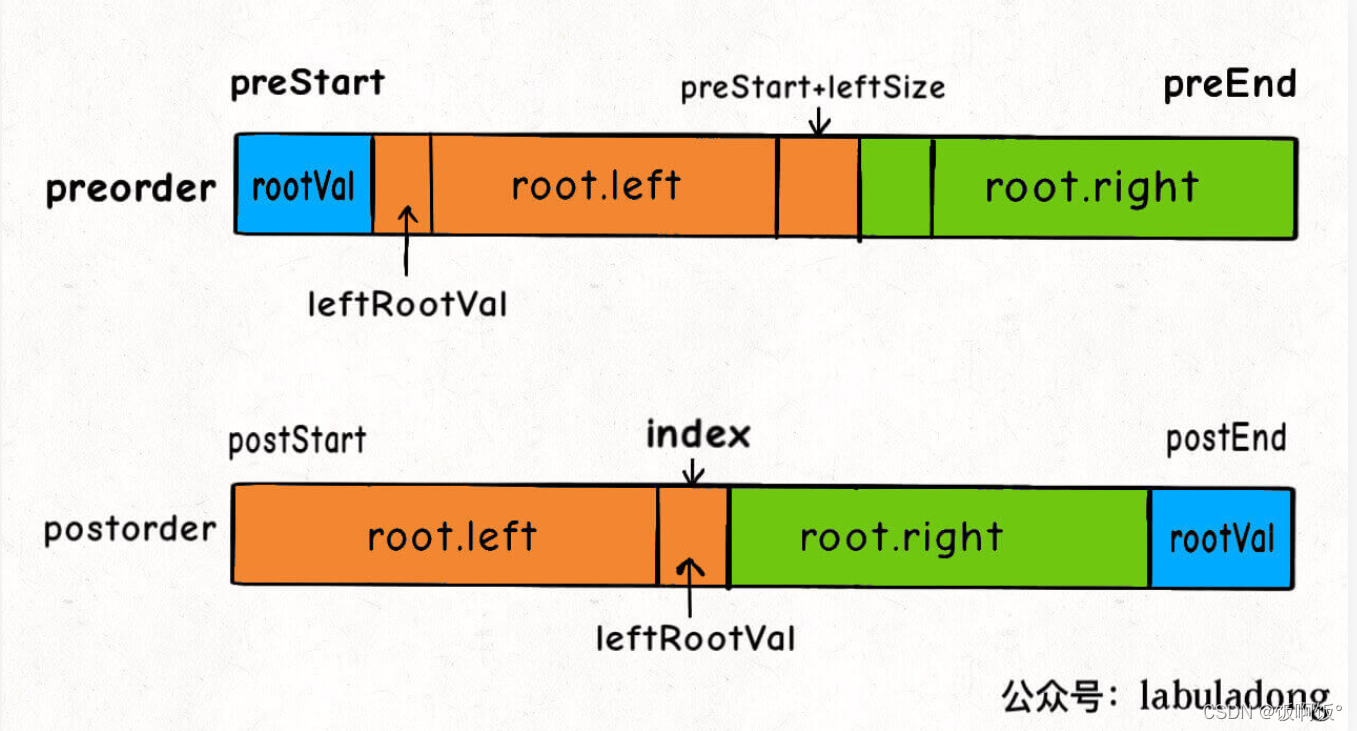
在这里插入图片描述
由于使用到了当前节点的下一节点,因此在判断条件那里也要加上一条如果perStart == preEnd,就应该创建节点,不用再遍历左右子树了.代码如下:

var constructFromPrePost = function(preorder, postorder) {
    return build(preorder,0,preorder.length-1,postorder,0,postorder.length-1)
};

var build = function(preorder,preStart,preEnd,postorder,postStart,postEnd){
    if(preStart > preEnd || postStart > postEnd){
        return null
    }
    if(preStart == preEnd){
        return new TreeNode(preorder[preStart])
    }
    var root = new TreeNode(preorder[preStart])
    var index = postorder.indexOf(preorder[preStart+1])
    var leftSize = index - postStart +1
    root.left = build(preorder,preStart+1,preStart+leftSize,postorder,postStart,index)
    root.right = build(preorder,preStart+leftSize+1,preEnd,postorder,index+1,postEnd-1)
    return root
}