LeetCode70.爬楼梯

思路：

先说一下这个题目吧，这是一个比较简单的题目，我曾在北京工业大学计算机考研的专业课见到过，也是比较热门的题目了。首先你下一次楼梯是有两种选择的，可以选择下一层或者下两层，而这两种选择又是分别作为一个新的问题对应两种选择，因此这道题可以直接采用递归的方式来写：

public static long climbStairs(int n) {//注意当n>45时，返回值会超过int类型的上限，可以用long来代替
        if(n>=2)//当楼梯层数大于1时，将问题分解为两个子问题
            return  climbStairs(n-1)+climbStairs(n-2);//递归，n层楼梯可分解为n-1层和n-2层两个子问题之和
        if(n==1||n==0)//问题终止条件，1层楼梯和0层楼梯只能有一种上楼方案
            return 1;
        else
            return 0;
    }

当我感觉这是一个很简单的题目时，却没通过测试：
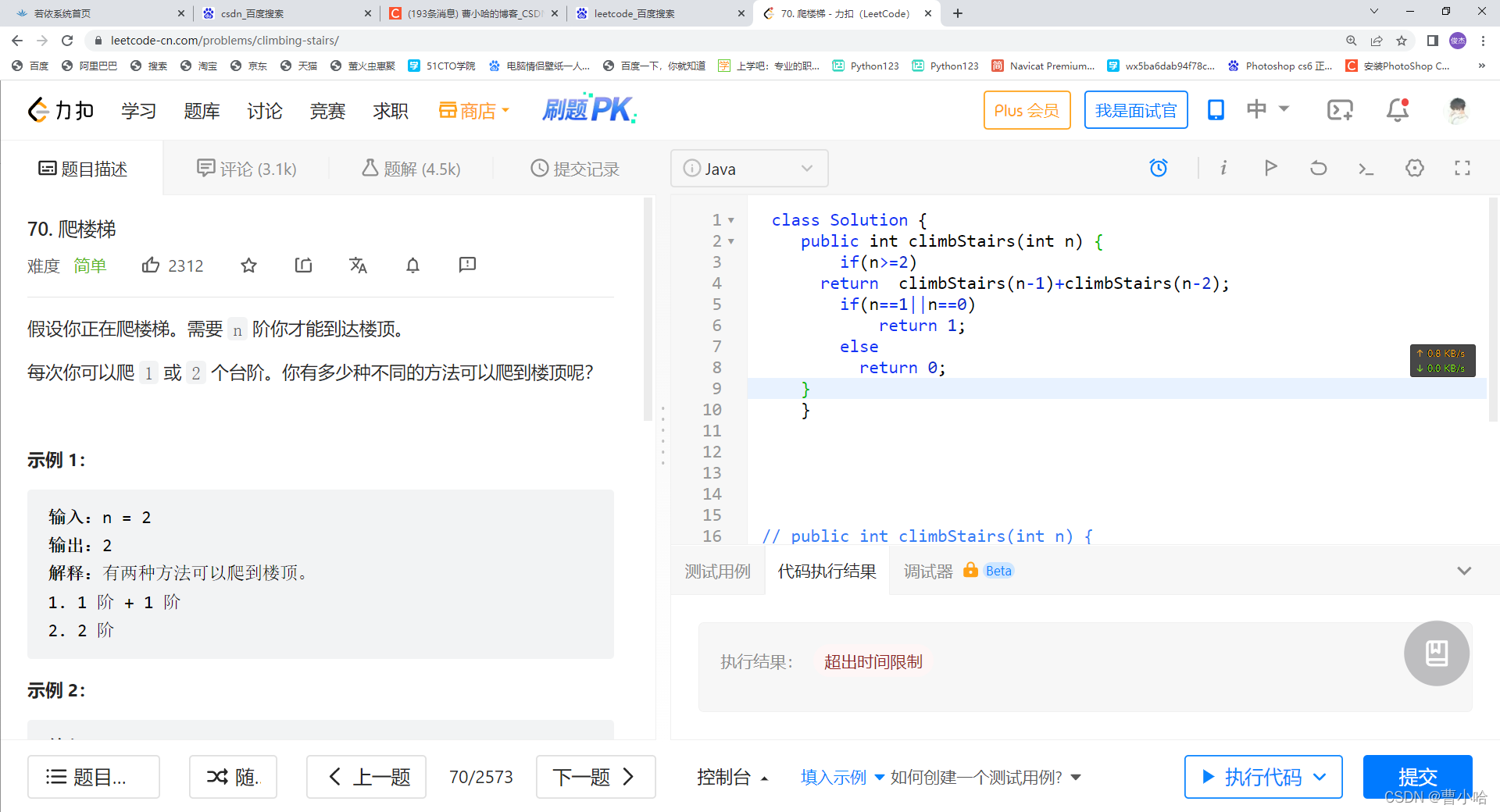
在这里插入图片描述
我们可以看到执行结果是超出时间限制，为了搞明白我的执行结果到底有没有出错，我把代码复制到IDEA里面进行测试，发现结果是正确的，然后我就开始思考怎么解决用时过长的问题。

发现问题：

由于递归是函数调用自身，而函数调用是有时间和空间的消耗的：每一次函数调用，都需要在内存栈中分配空间以保存参数、返回地址以及临时变量，而往栈中压入数据和弹出数据都需要时间，这就导致了程序运行时间过大。

解决问题：

既然知道了是递归的原因，那么解决方法就简单了，把递归转化为非递归就可以了。刚才的递归算法是从n阶楼梯出发，逐步分解为低阶楼梯，直至到最后两层楼梯，而非递归就要改为从前两层出发，逐步推算出高阶楼梯所有的爬楼梯方案。

 public int climbStairs(int n) {
        if(n<=2)return n;//当n小于等于2时，楼梯层数即为上楼方案数
     int a1=1,a2=2;
     for(int i=3;i<=n;i++)//采用数学形式的递推式，a2即为n层楼的上楼方案数
     {
         int temp=a1+a2;
         a1=a2;
         a2=temp;
     }
     return a2;
 }

最后成功通过了测试：
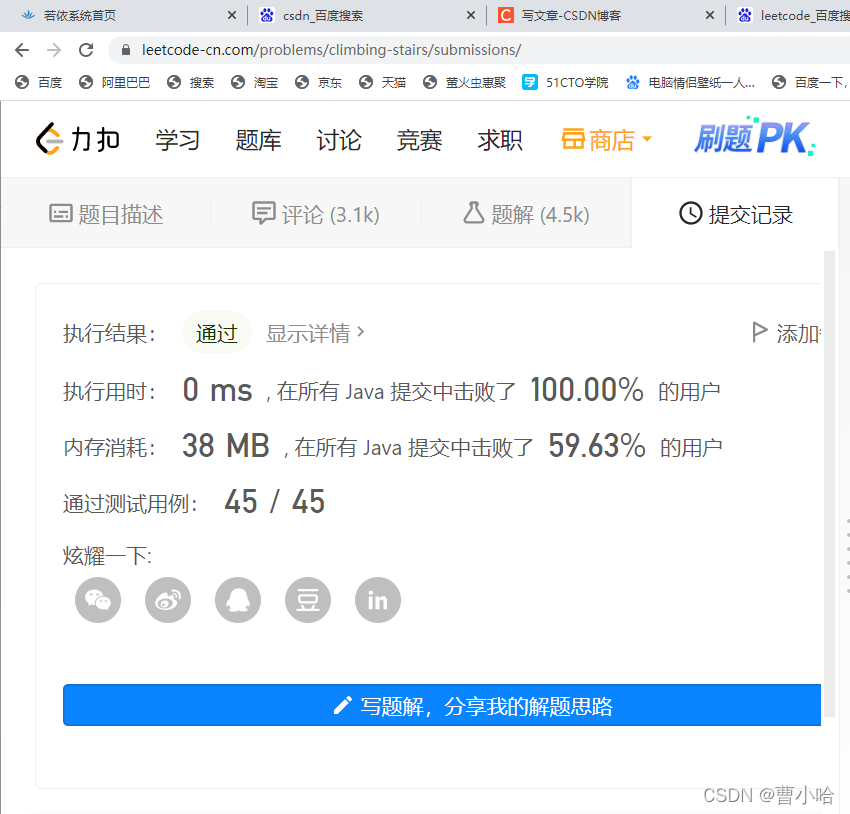
在这里插入图片描述