前言
数据库中最重要的基础是索引,索引为什么能被建立起来,因为能建立索引的字段都是可以排序的,(任何字符串都可以排序)只是我们平时感受不深。
排序是如何帮助加速找数据库里的东西的呢?
在数据库里存数据的方式真的有可能是有顺序的。比如数据库里面硬盘结构可能就有顺序。底层数据写在硬盘上是顺序的话,就在底层数据之上建出一颗索引树。
搜索二叉树(BST)
搜索二叉树单纯的加数据,找数据很容易,所以搜索二叉树本身就可以支持索引。(增删改查都在树上玩)
但问题是,在最坏情况下,这棵树会退化成为链表。
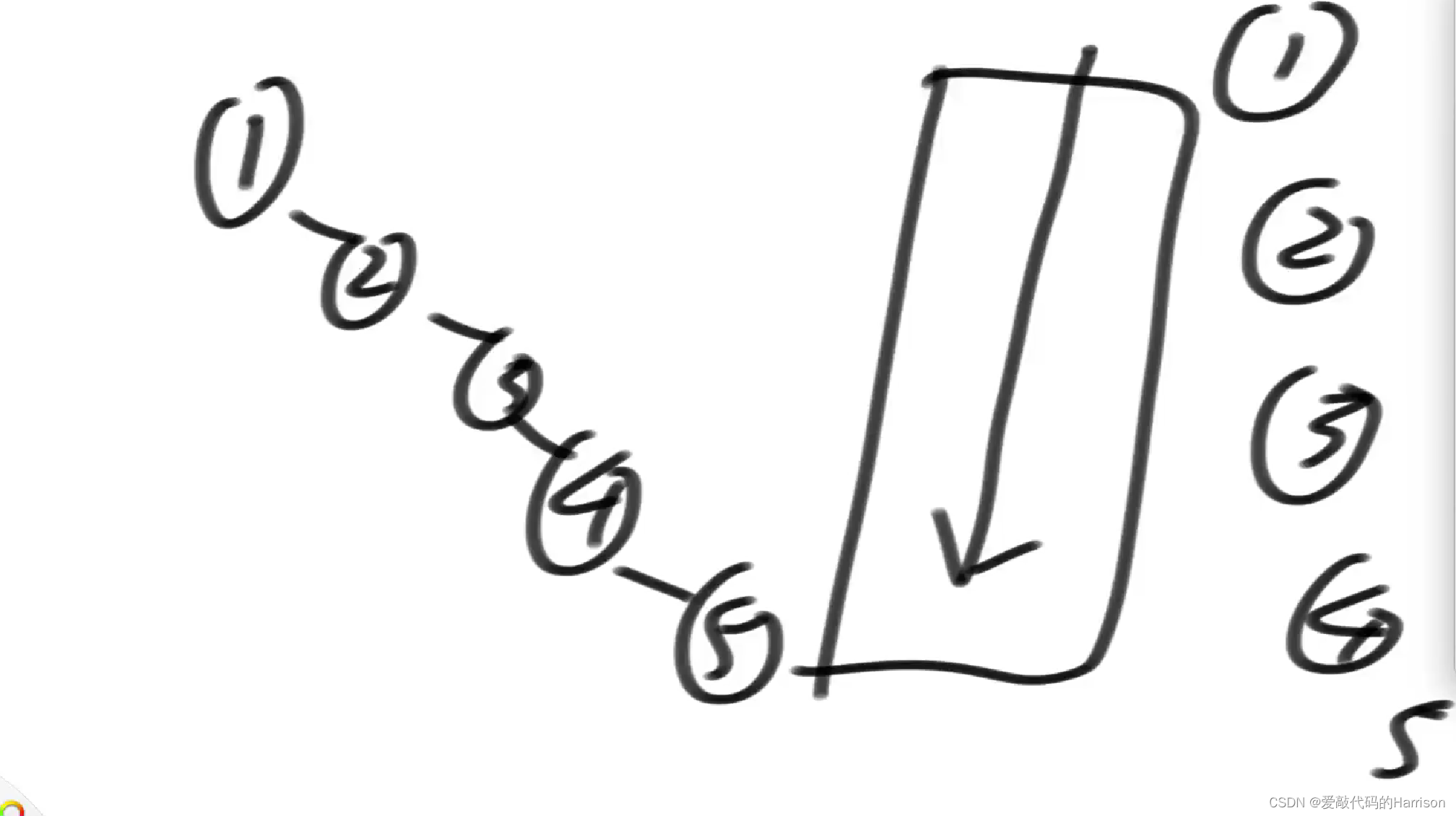
这个时候就引出了平衡搜索二叉树的概念:一棵树先保证是搜索二叉树的情况下,再保证它的平衡性。所谓平衡性:假设所有数据量为N的话,树的最大高度也仅仅是LogN的水平。
为什么不用哈希表(O(1))?因为现实情况下在数据库里的操作是有联系的,比如范围查询。
平衡搜索二叉树(AVL)
平衡搜索二叉树的基础操作,左旋和右旋,(左旋和右旋都不会破坏原本的搜索性)
头结点往哪左边倒就是左旋,头结点往右边倒就是右旋。
左旋
左旋:先指定头结点,然后,头结点往左边倒,头结点的右孩子上来
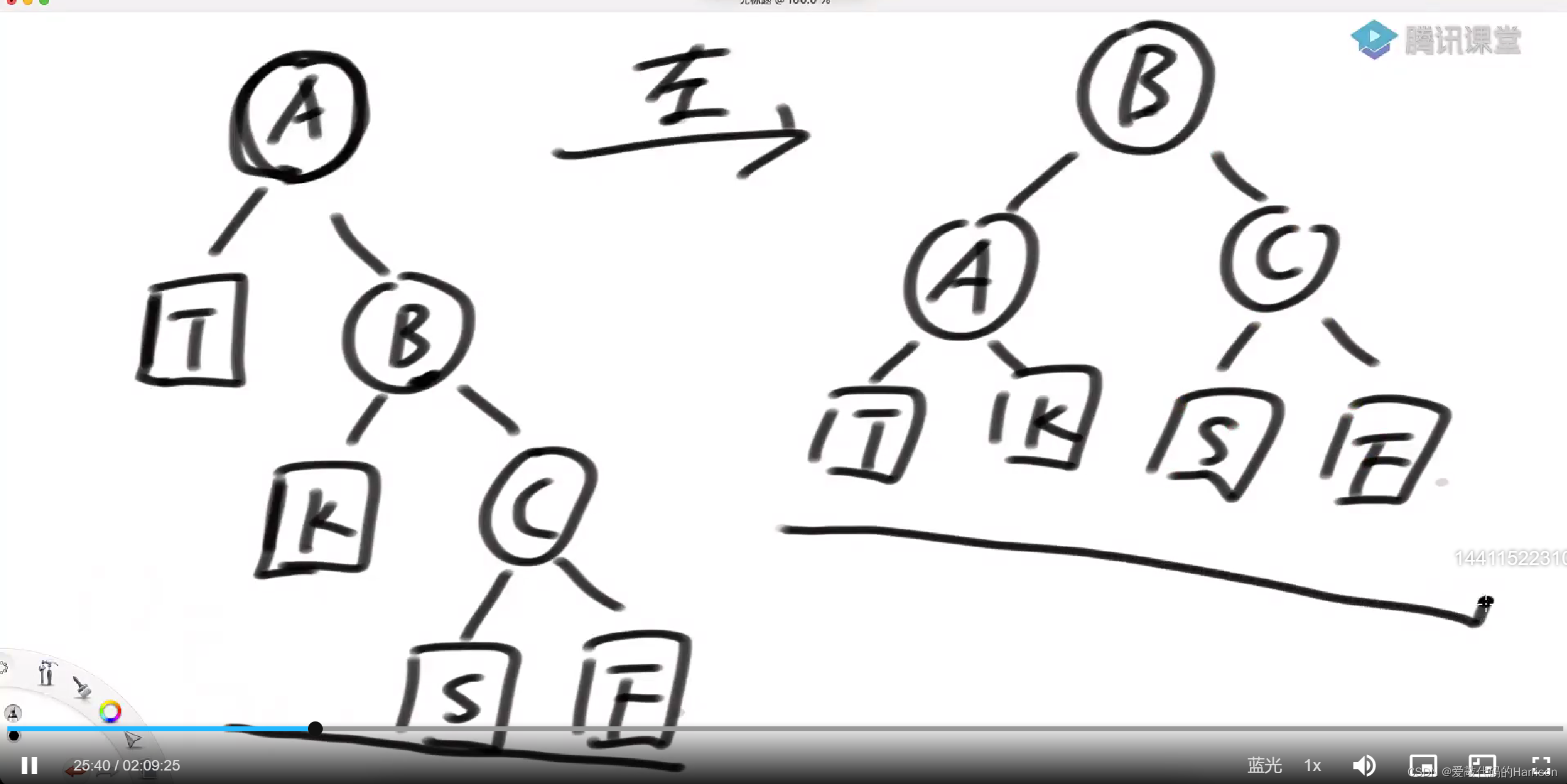
右旋
右旋:头结点往右边倒,头结点的左孩子上来。
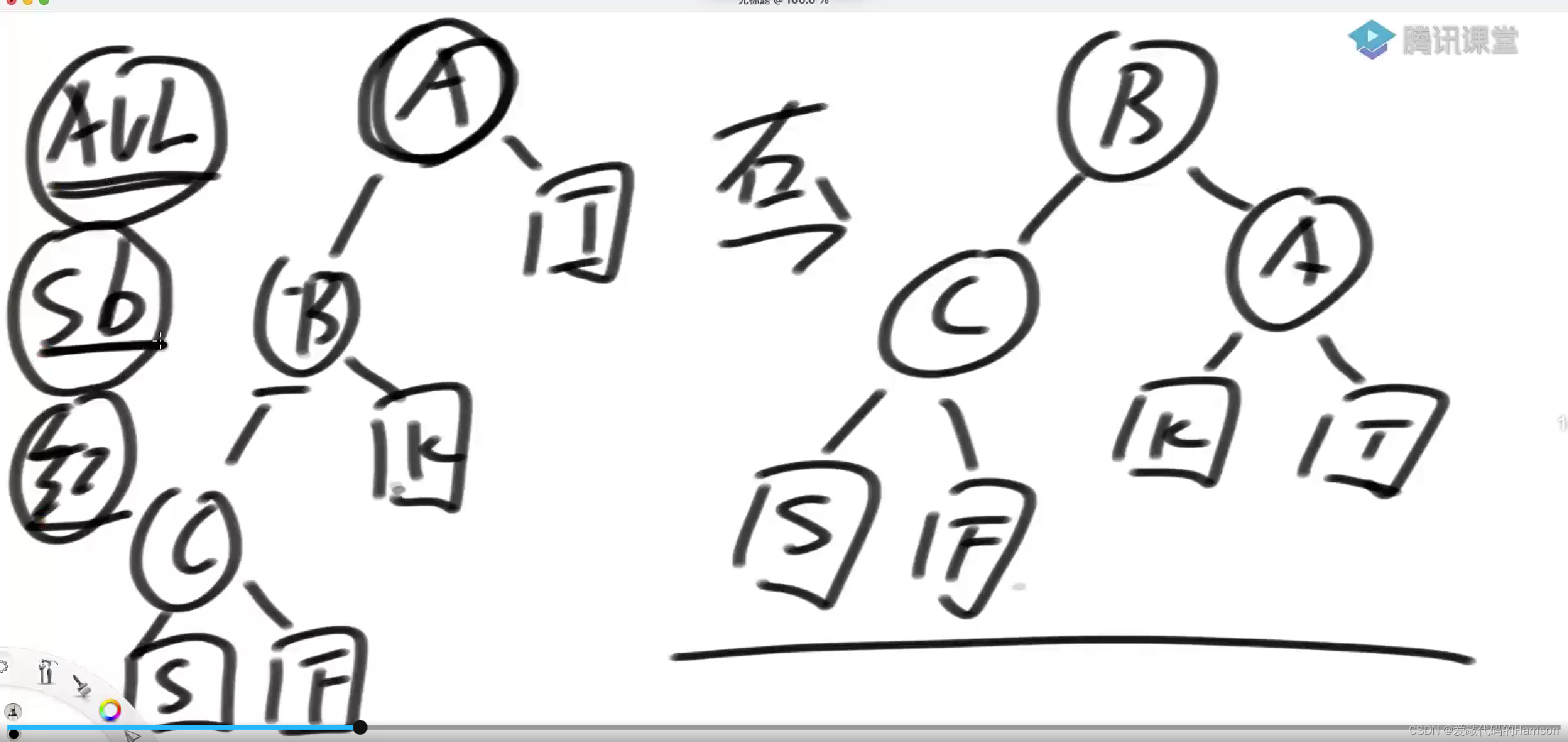
总结:经典的有序表有很多种实现方式,比如AVL树,SB树(size balance tree),红黑树等,但是不管是哪种平衡搜索二叉树,不管平衡性如何定义,底层让它们变平衡的方式只有左旋和右旋!
AVL树(平衡性最严苛)
为什么要有AVL树,因为AVL树的平衡性会使得在树上玩增删改查的效率会更高!!!
AVL树的平衡性:任何一个结点,|左树最大高度 - 右树最大高度| < 2
搜索二叉树添加结点很容易,但是删除结点并不那么容易,在coding上都是要花费很大功夫的。

搜索二叉树删除结点最麻烦的一种情况,就是要删除的结点既有左树,也有右树。 可以用要删除结点右树上的最左结点替换,也可以用左树上的最右结点替换。下面介绍用右树上的最左替换。
如下图,要删除的结点是X,找到X结点右树上最左边的结点a,覆盖X。这样,左右两边的搜索性都没有被破坏。因为在一课搜索二叉树中,a结点就是距离X结点最近且比它大的结点,这是搜索二叉树的性质。
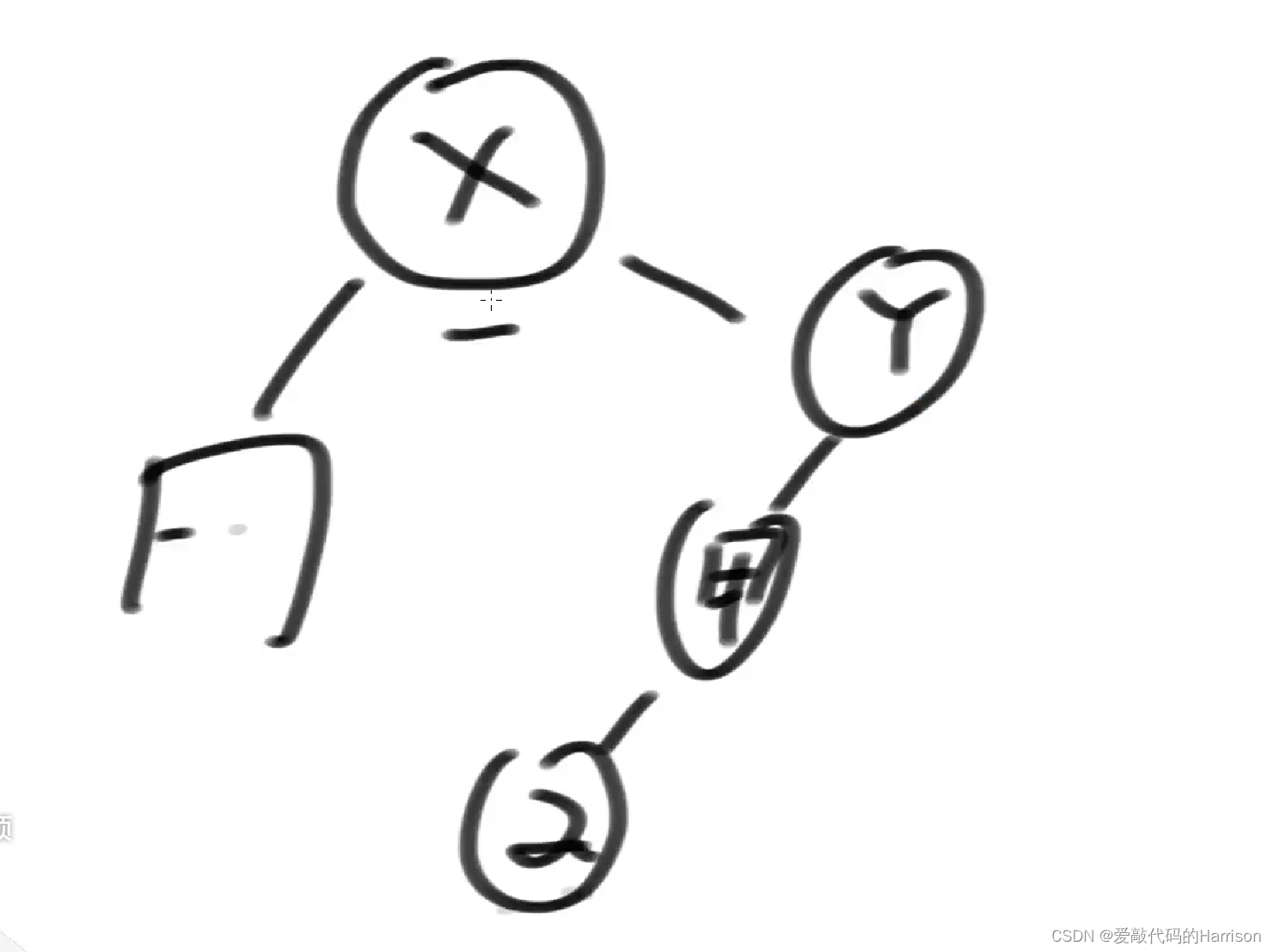
上面介绍了搜索二叉树的删除是如何进行的,当然,添加和查都很容易。AVL树,的添加,删除和查都跟搜索二叉树一样,只是在进行完了这些操作后,AVL树有自己平衡性的补充。
AVL树的平衡性
破坏AVL树平衡性的四种类型
那么AVL树如何调整平衡性?跟破坏AVL平衡性的类型有关。AVL树破坏平衡性的类型有如下四种(跟左旋和右旋无关):
以下是AVL树局部破坏平衡性的情况
- LL型
- LR型
- RR型
- RL型
LL型违规
遇到LL型违规,做一次右旋即可恢复平衡性,遇到RR型,做一次左旋即可。
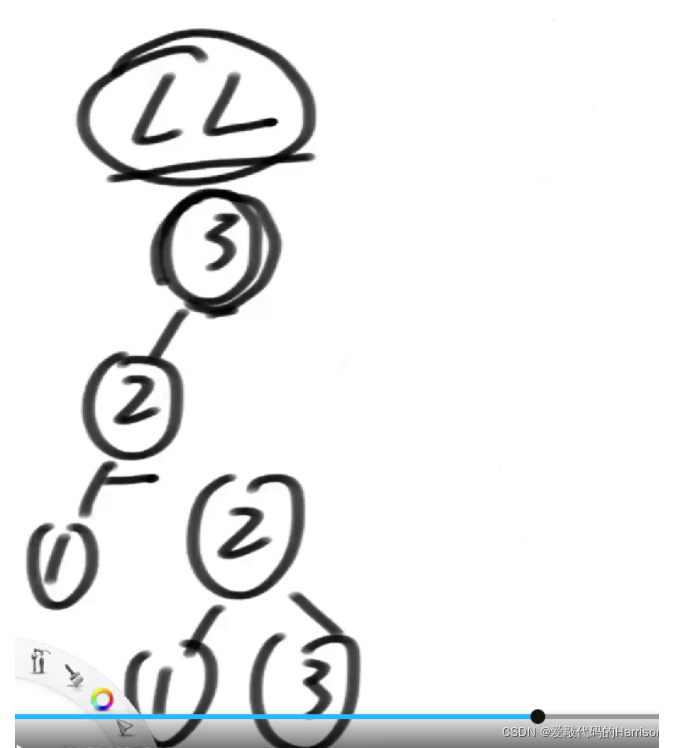
LR型违规
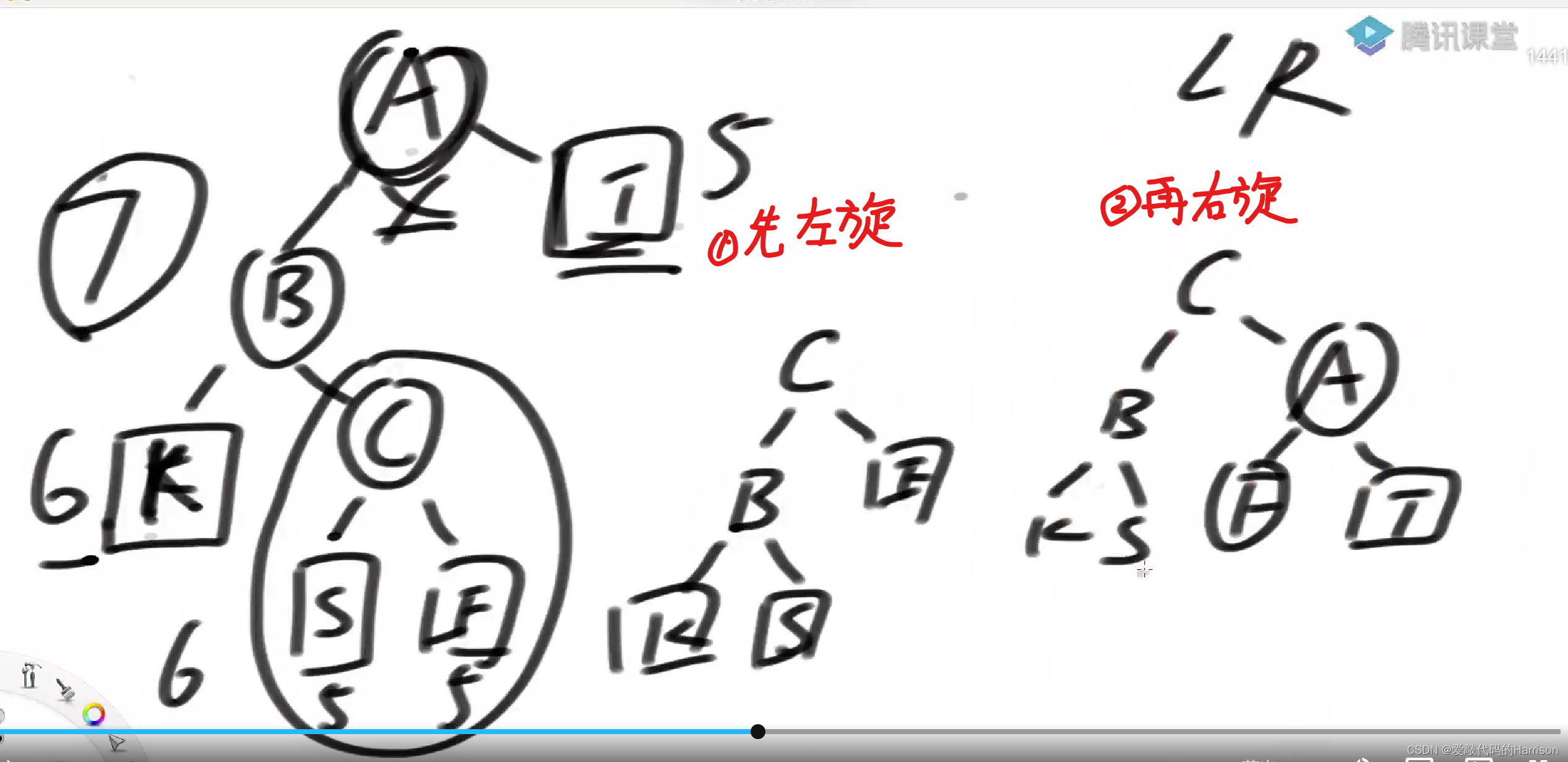
遇到LR型违规,如下图,右树的高度比较小,左树的高度比较大,并且是由于左树的右树高度比较大,才破坏的平衡性。
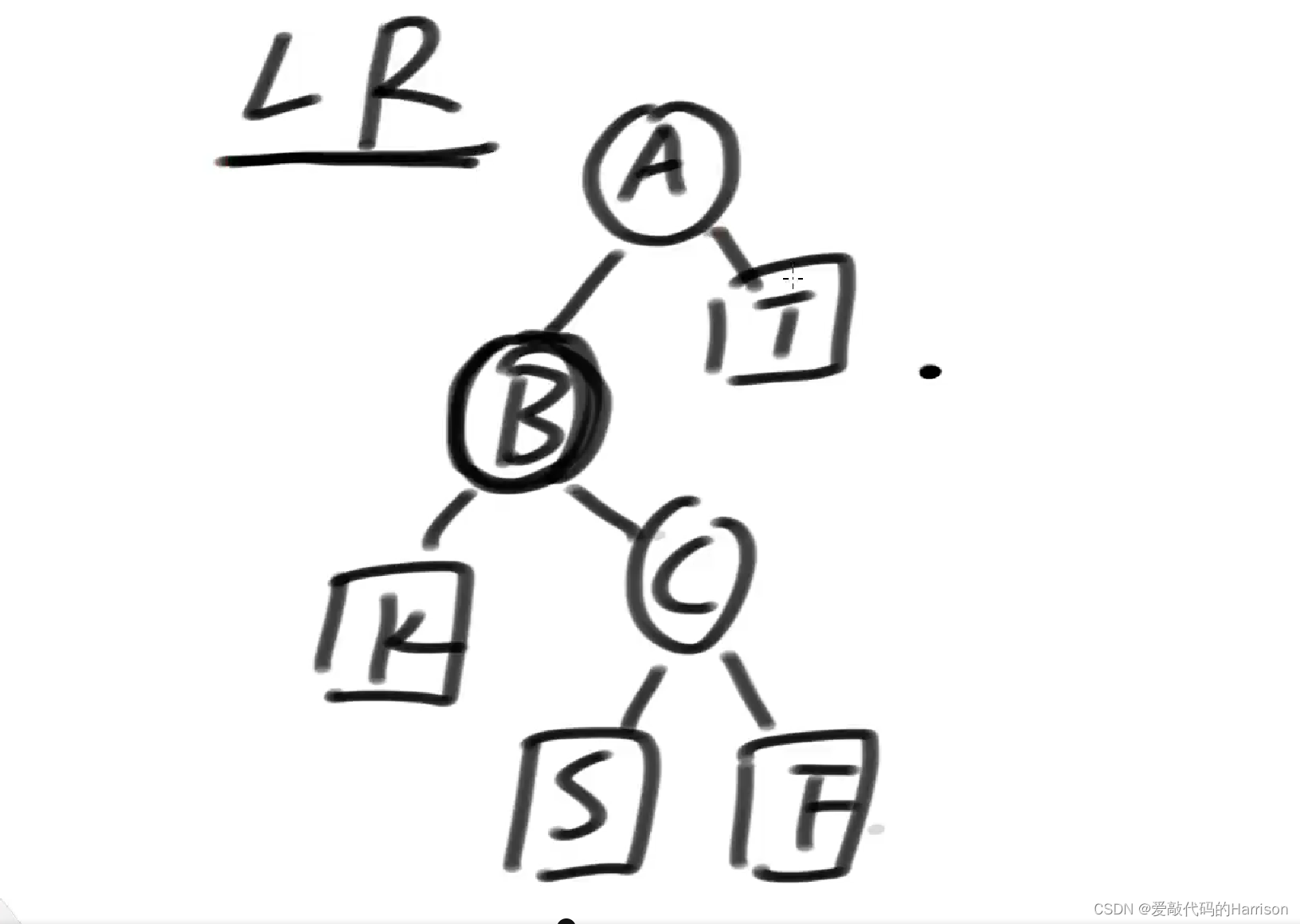
如何调整,想办法让孙子替换爷爷,也就是说让C替换A。
第一步:在以B为头结点的整棵树上做一次左旋,让C先往上走一步。
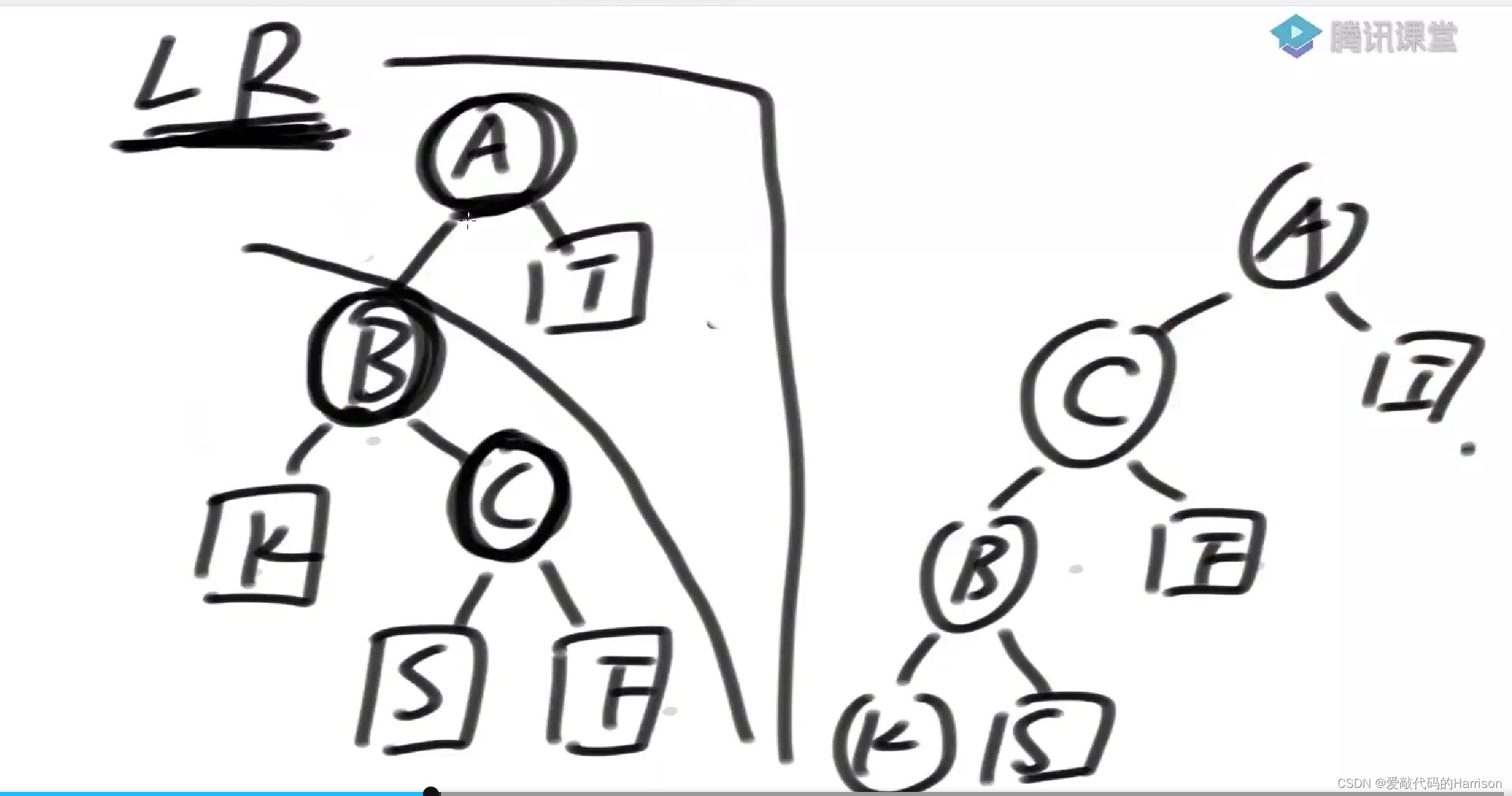
第二步:在以A为头结点的整棵树进行一次右旋,让C彻底来到头部。
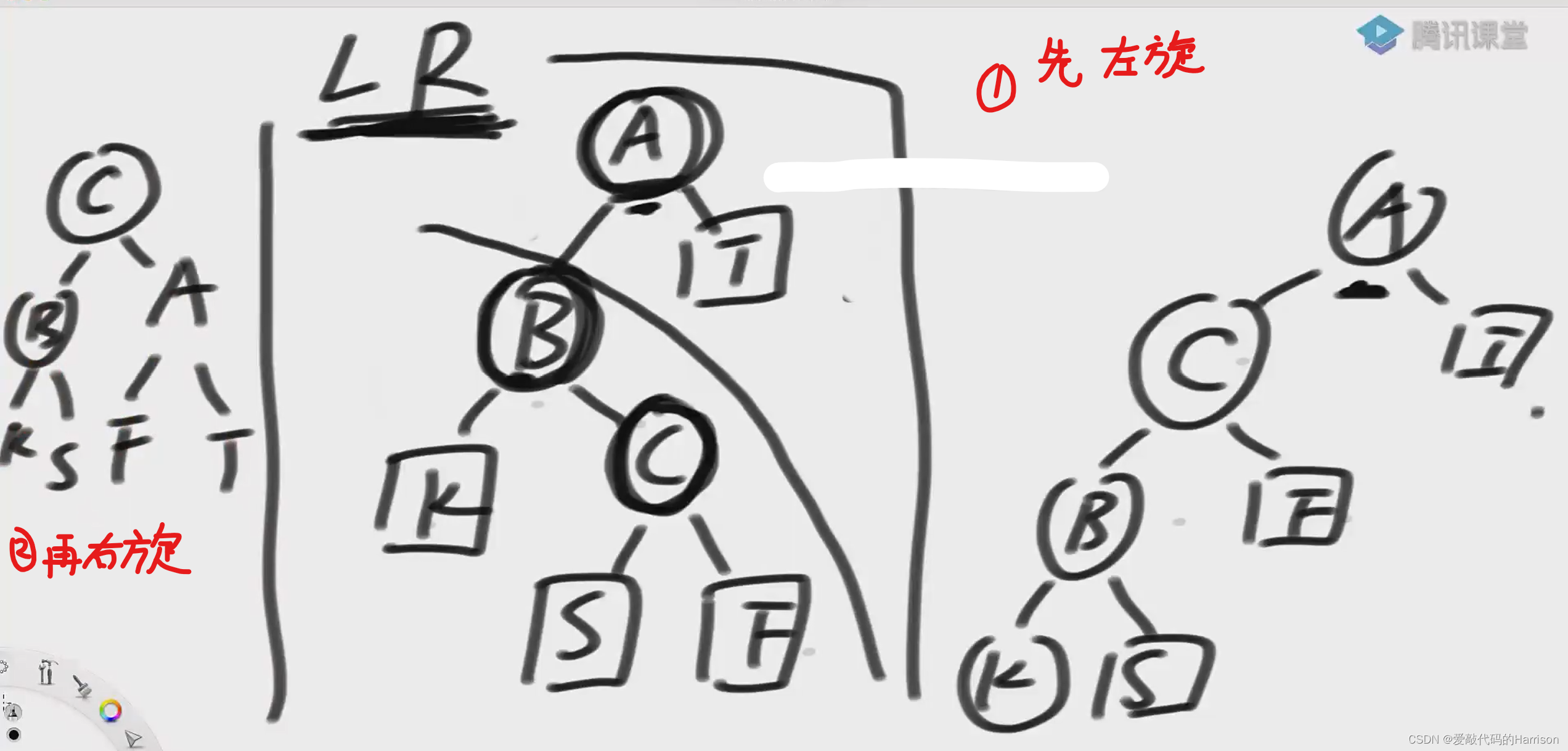
RR型违规
RR型:做一次左旋即可
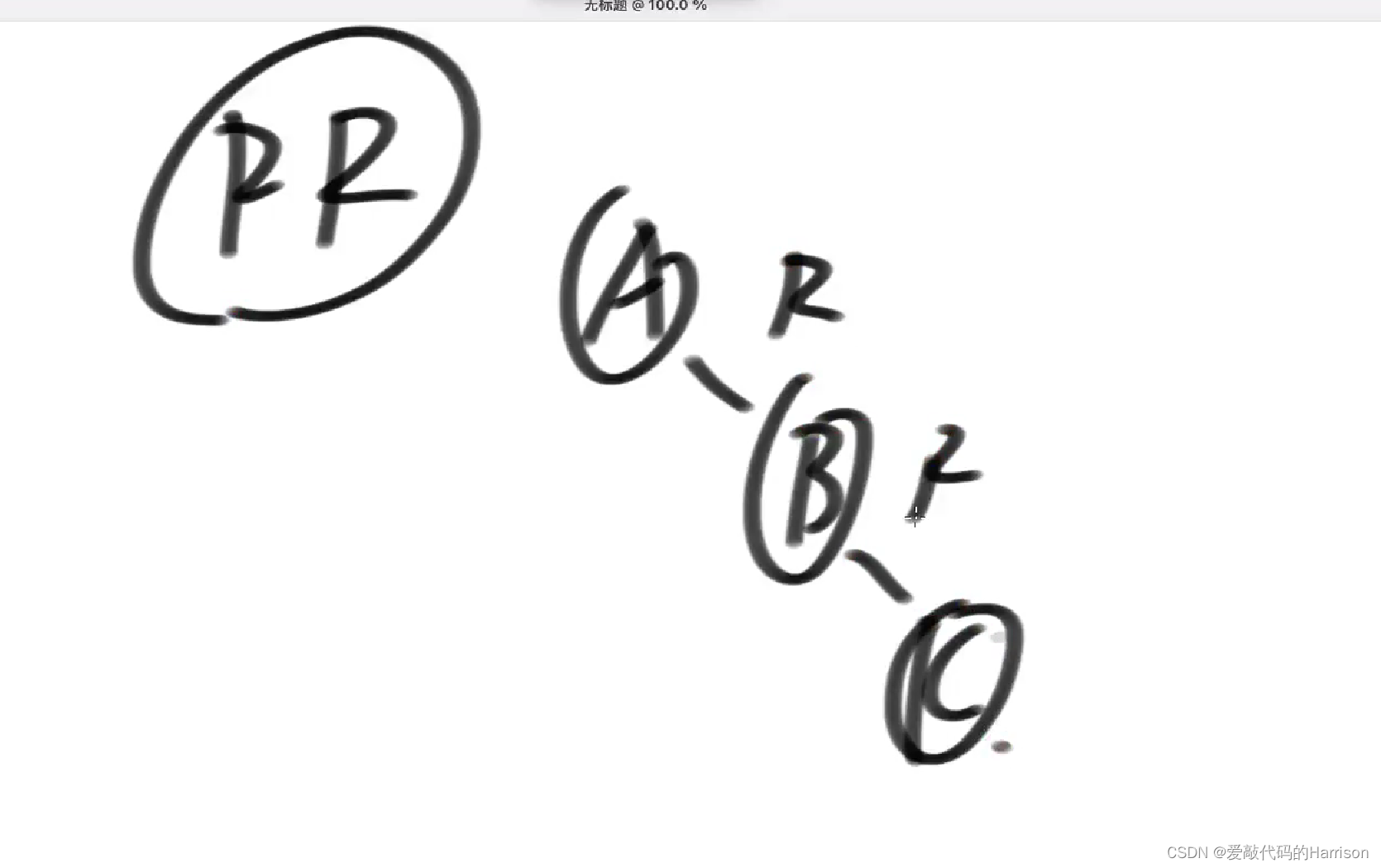
RL型违规
RL型:想办法让孙子去到顶部,也就是说C结点替换A。(C就是孙)
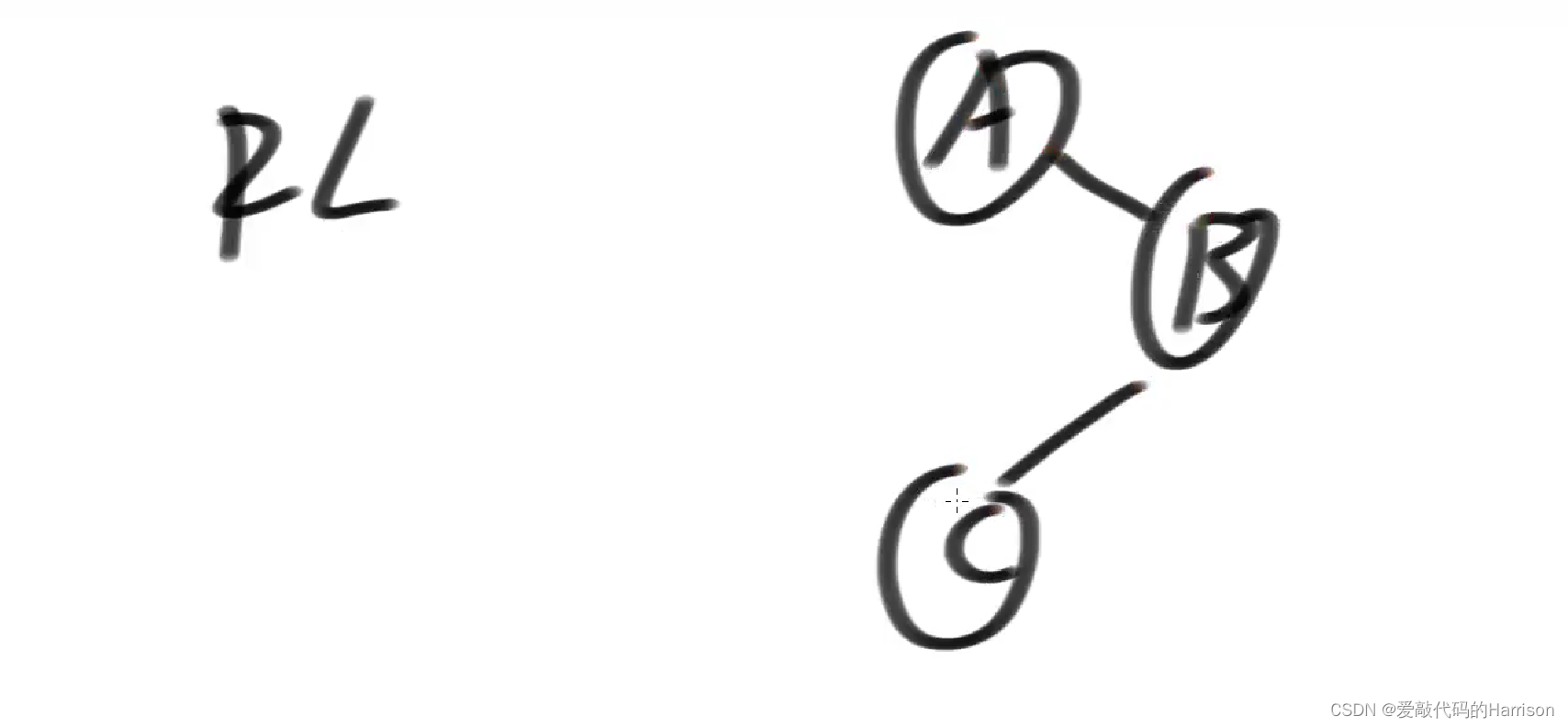
第一步:先在以B为头结点的整棵树玩一次右旋
第二步:在以A为头结点整棵树玩一次左旋
极端情况
但是存在一种极端情况,既属于LL违规型,又属于LR违规型。
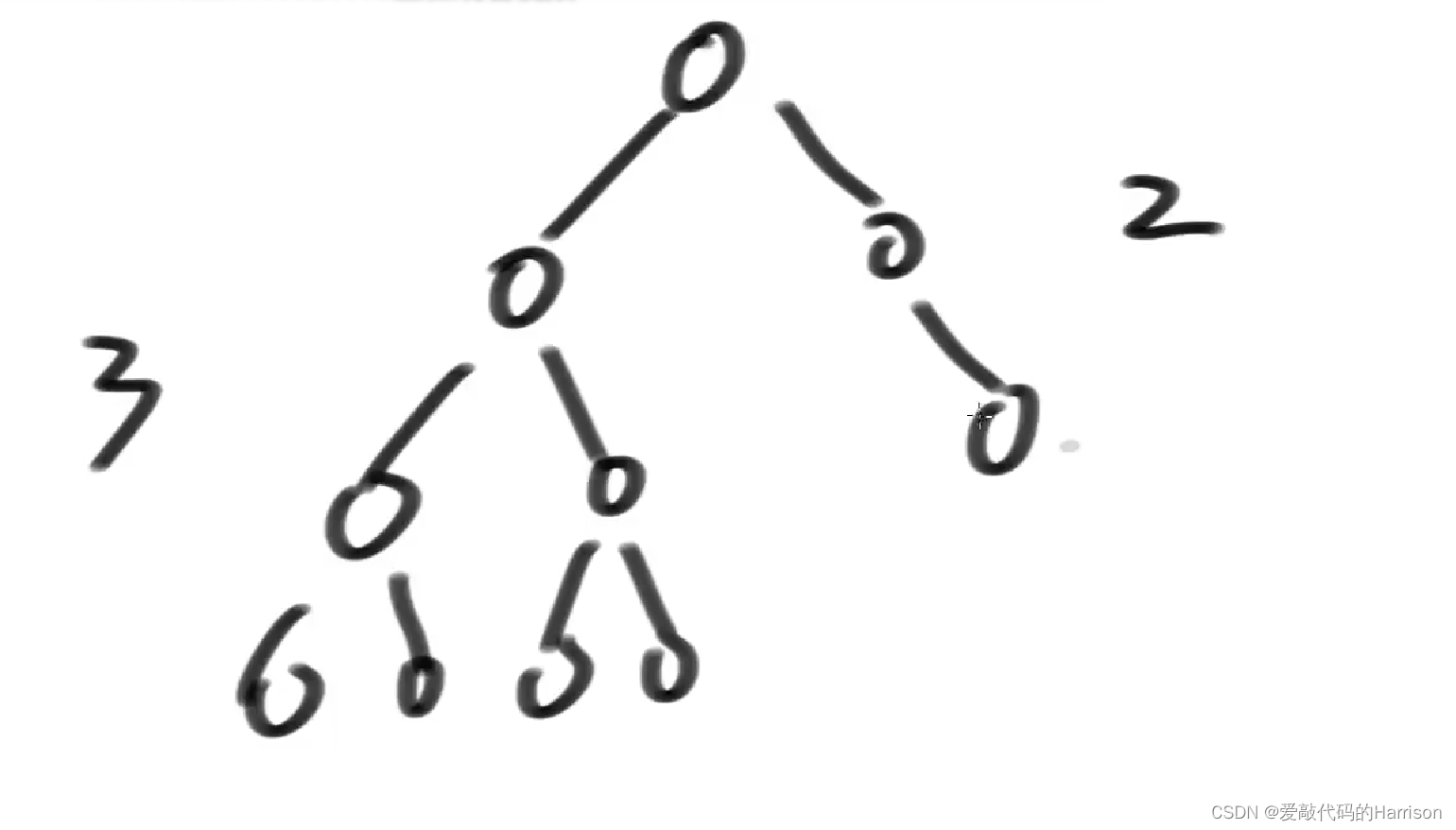
上图中的树,删掉右边一个结点后,就破坏平衡性,并且既是LL,又是LR。
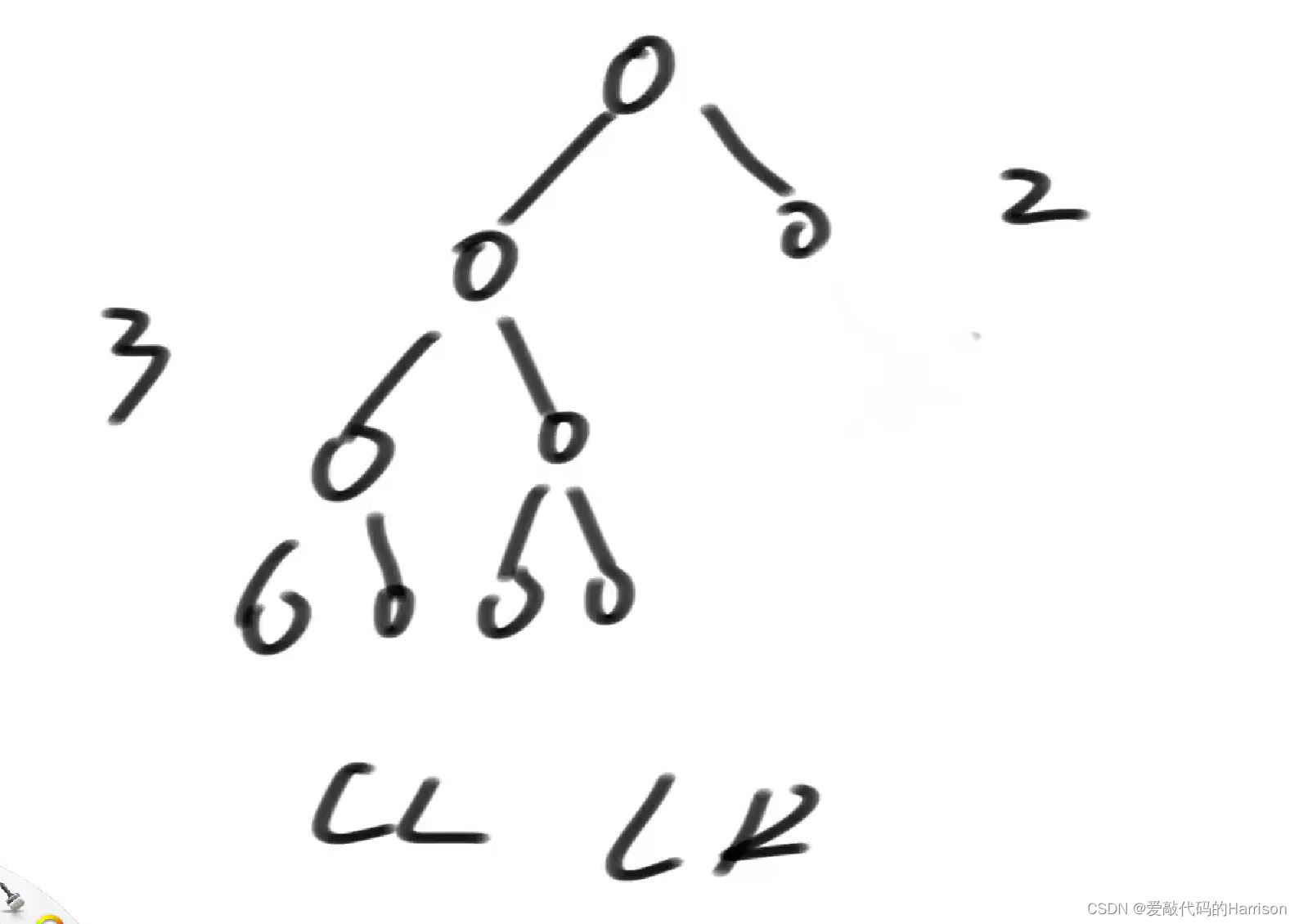
既是LL又是LR,直接按照LL型标准来调整,直接右旋。是正确的!
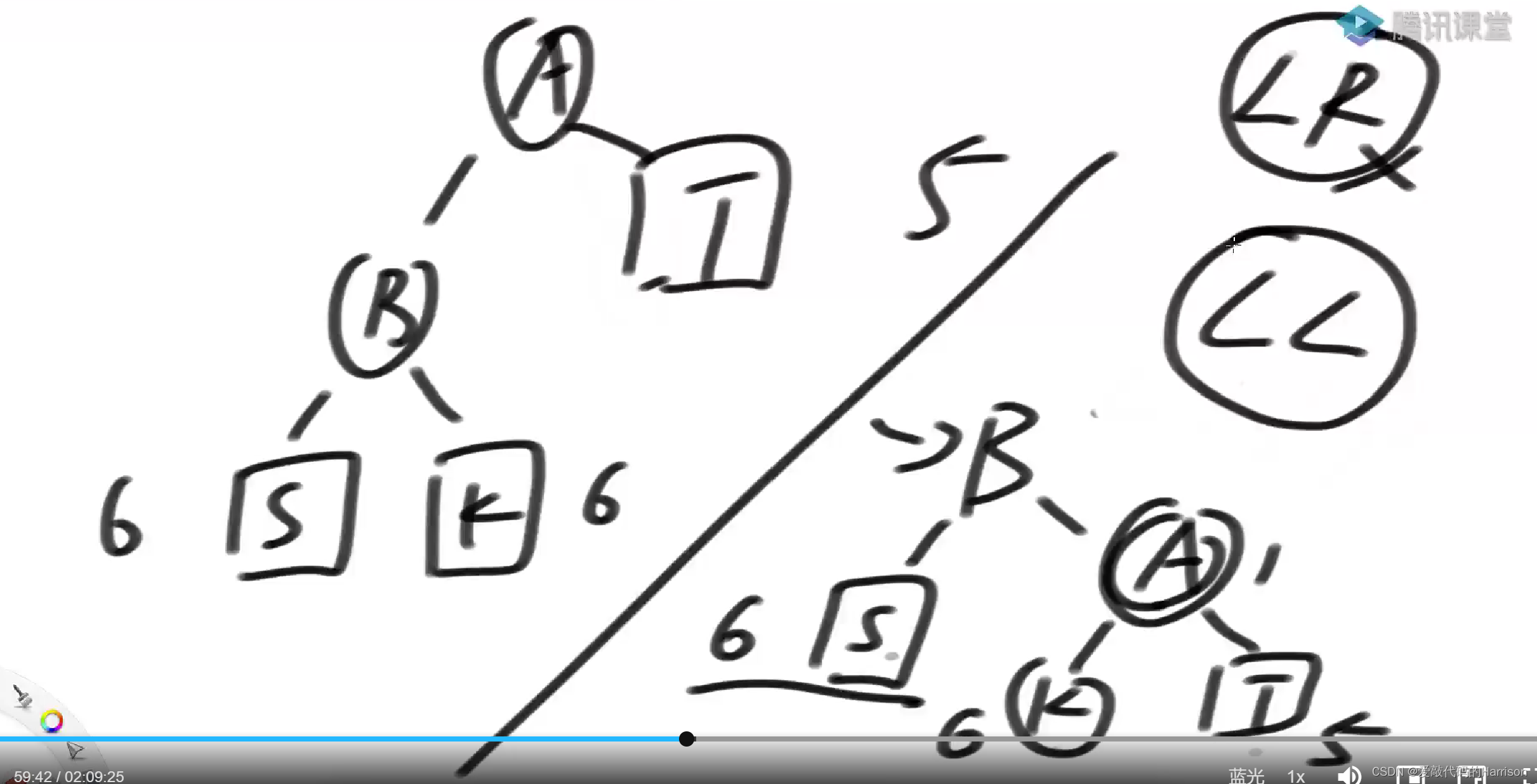
举个反例,既是LL型,又是LR型(下图A的整颗左树高度是7,整颗右树高度是5)按照LR型标准来调整是错误的。
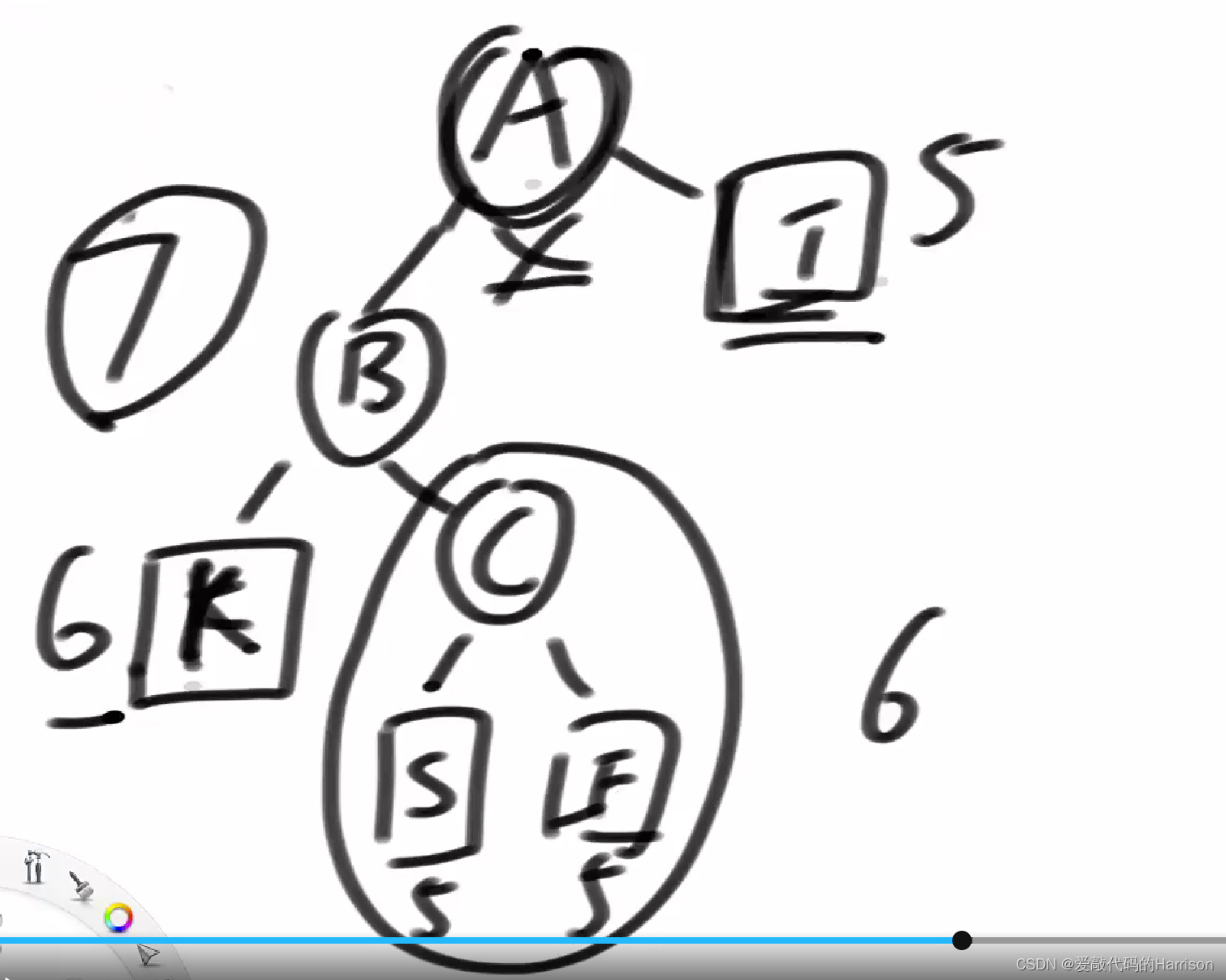
上图例子按照LL型调整后是正确的。
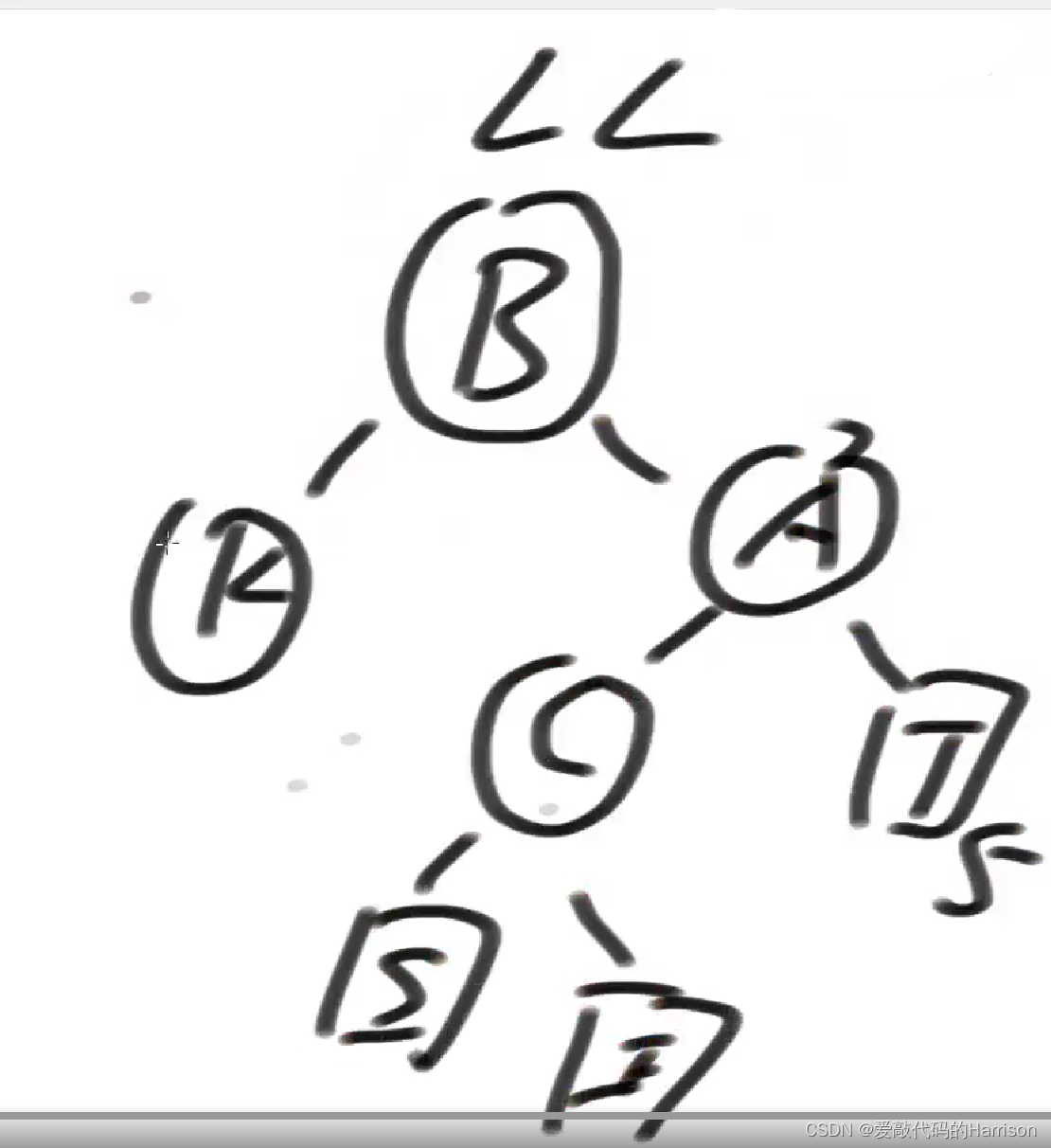
但是按照LR型调整是错误的。虽然下面例子(S的高度是5)是正确的,但是如果S的高度是4的话,依然破坏了平衡性。
如果S高度是4,按照LL型标准调整,依然正确,按照LR调整是错误的!!!,可以自己动手画一下试试。
同理,也会出现既是RL型违规和又是RR型违规。但是不会出现既是LL型,又是RR型。
AVL树的调整代价
上述四种违规类型的调整代价都是很小的,O(1)。
那么AVL树加入一个结点后,具体如何调整呢?是加入某个结点后,往上沿途每个结点都检查,看属于哪种违规类型。包括加入的结点。
如果AVL树在加入结点之前的最大高度为LogN,那么加入一个结点后,即使往上所有结点都要检查是否违规,因为上面只有LogN个结点,而每个节点的调整代价为O(1);所以,AVL树调整平衡性的代价就是O(LogN)
AVL树里,维持平衡的因子就是树的高度h,所以每一次结点相对位置调整完后,都要更新平衡因子h。如果别的树的平衡因子是另外的,也要这么干,比如红黑树,SB树等,后续文章会讲述到。
补充
有序表跟AVL树的关系
如果将有序表比作成一个接口,那么AVL树就是一个具体的类,而可以实现有序表的还有SB树,红黑树,跳表,234树,B树,B+树…,它们实现有序表的时间复杂度都是O(LogN),区别只是具体的实现细节不一样。
今天为什么关系型数据库走向了没落,随之流行的是水平扩展性数据库,一致性哈希数据库。待到后续文章继续了解吧
最后附上全部代码~
package com.harrison.class25;
/**
* @author Harrison
* @create 2022-04-03-10:46
* @motto 众里寻他千百度,蓦然回首,那人却在灯火阑珊处。
*/
public class Code01_AVLTreeMap {
/*
因为AVL树是有序表里面用到的,所以必须要求它的key可比较
没有办法比较,就不用谈有序表
*/
public static class AVLNode<K extends Comparable<K>, V> {
// AVL里的具体结点封装进去
public K k;
public V v;
// 指向左孩子和右孩子的结点
public AVLNode<K, V> l;
public AVLNode<K, V> r;
// AVL树中的平衡因子:高度(整棵AVL树的高度)
public int h;
public AVLNode(K key, V value) {
k = key;
v = value;
h = 1;
}
}
/*
用AVL树实现的有序表
*/
public static class AVLTreeMpa<K extends Comparable<K>, V> {
public AVLNode root;// 整棵树的根结点
public int size;// 加入的key的个数
public AVLTreeMpa() {
root = null;
size = 0;
}
// 针对cur结点整棵树玩右旋
private AVLNode<K, V> rightRotate(AVLNode<K, V> cur) {
// 先记住cur的左孩子,因为右旋是cur往右边倒
AVLNode<K, V> left = cur.l;
// 然后左孩子的右树挂在我的(cur)的左边
cur.l = left.r;
// 左孩子的右接管cur
left.r=cur;
// 调整cur和left的高度
// 并且一定要先调整cur的高度后再调整left
// 因为右旋后头结点是left了
cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
left.h = Math.max((left.l != null ? left.l.h : 0), (left.r != null ? left.r.h : 0)) + 1;
return left;
}
private AVLNode<K,V> leftRotate(AVLNode<K,V> cur){
AVLNode<K,V> right=cur.r;
cur.r=right.l;
right.l=cur;
cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
right.h = Math.max((right.l != null ? right.l.h : 0), (right.r != null ? right.r.h : 0)) + 1;
return right;
}
/*
搜索二叉树里不加重复的key
只要说搜索二叉树,它的潜台词就是每个key都不一样
*/
// 在以cur为头的整颗子树上,加记录,并且把整棵树的头结点返回
// add()方法不会遇到相同的key
public AVLNode<K,V> add(AVLNode<K,V> cur,K key,V value){
if(cur==null){
return new AVLNode<K,V>(key,value);
}else{
if(key.compareTo(cur.k)<0){
// 有可能存在换头的情况
cur.l=add(cur.l,key,value);
}else{
cur.r=add(cur.r,key,value);
}
}
cur.h = Math.max((cur.l != null ? cur.l.h : 0), (cur.r != null ? cur.r.h : 0)) + 1;
// 以上只是搜索二叉树的增加结点
// 加完结点后,调平衡
return maintain(cur);
}
// 在cur这棵树上,删掉key所代表的节点
// 返回cur这棵树的新头部
private AVLNode<K,V> delete(AVLNode<K,V> cur,K key){
if(key.compareTo(cur.k)>0){
cur.r=delete(cur.r,key);
}else if(key.compareTo(cur.k)<0){
cur.l=delete(cur.l,key);
}else{
if(cur.l==null && cur.r==null){
cur=null;
}else if(cur.l==null && cur.r!=null){
cur=cur.r;
}else if(cur.l!=null && cur.r==null){
cur=cur.l;
}else{
// 找到右树上的最左结点
AVLNode<K,V> des=cur.r;
while (des.l!=null){
des=des.l;
}
/*
先在右树调一个delete()方法,在删掉最左结点后,完成右树的平衡调整,
然后得到最左结点,替换要删除的结点,然后依次往上检查平衡性
*/
cur.r=delete(cur.r,des.k);
des.l=cur.l;
des.r=cur.r;
cur=des;
}
}
if (cur != null) {
cur.h = Math.max(cur.l != null ? cur.l.h : 0, cur.r != null ? cur.r.h : 0) + 1;
}
// 每删掉一个结点都会往上检查平衡性,所以递归函数会多次调用自己,而每一次都会检查自己的平衡性
return maintain(cur);
}
private AVLNode<K,V> maintain(AVLNode<K,V> cur){
if(cur==null){
return null;
}
int leftHeight=cur!=null?cur.l.h:0;
int rightHeiht=cur.r!=null?cur.r.h:0;
if(Math.abs(leftHeight-rightHeiht)>1){
if(leftHeight>rightHeiht){
int leftLeftHeight = cur.l != null && cur.l.l != null ? cur.l.l.h : 0;
int leftRightHeight = cur.l != null && cur.l.r != null ? cur.l.r.h : 0;
if(leftLeftHeight>leftRightHeight){
// 等于为什么放在这里,因为既是LL型,又是LR型,按照LL型标准来调整平衡性
cur=rightRotate(cur);
}else{
cur.l=leftRotate(cur.l);
cur=rightRotate(cur);
}
}else{
int rightLeftHeight = cur.r != null && cur.r.l != null ? cur.r.l.h : 0;
int rightRightHeight = cur.r != null && cur.r.r != null ? cur.r.r.h : 0;
if(rightLeftHeight>=rightRightHeight){
// 同理,如果既是RR型,又是RL型,按照RR型标准来调整平衡性
cur=leftRotate(cur);
}else{
cur.r=rightRotate(cur.r);
cur=leftRotate(cur);
}
}
}
return cur;
}
private AVLNode<K, V> findLastIndex(K key) {
AVLNode<K, V> pre = root;
AVLNode<K, V> cur = root;
while (cur != null) {
pre = cur;
if (key.compareTo(cur.k) == 0) {
break;
} else if (key.compareTo(cur.k) < 0) {
cur = cur.l;
} else {
cur = cur.r;
}
}
return pre;
}
private AVLNode<K, V> findLastNoSmallIndex(K key) {
AVLNode<K, V> ans = null;
AVLNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.k) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.k) < 0) {
ans = cur;
cur = cur.l;
} else {
cur = cur.r;
}
}
return ans;
}
private AVLNode<K, V> findLastNoBigIndex(K key) {
AVLNode<K, V> ans = null;
AVLNode<K, V> cur = root;
while (cur != null) {
if (key.compareTo(cur.k) == 0) {
ans = cur;
break;
} else if (key.compareTo(cur.k) < 0) {
cur = cur.l;
} else {
ans = cur;
cur = cur.r;
}
}
return ans;
}
public int size() {
return size;
}
public boolean containsKey(K key) {
if (key == null) {
return false;
}
AVLNode<K, V> lastNode = findLastIndex(key);
return lastNode != null && key.compareTo(lastNode.k) == 0 ? true : false;
}
public void put(K key, V value) {
if (key == null) {
return;
}
AVLNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.k) == 0) {
lastNode.v = value;
} else {
size++;
root = add(root, key, value);
}
}
public void remove(K key) {
if (key == null) {
return;
}
if (containsKey(key)) {
size--;
root = delete(root, key);
}
}
public V get(K key) {
if (key == null) {
return null;
}
AVLNode<K, V> lastNode = findLastIndex(key);
if (lastNode != null && key.compareTo(lastNode.k) == 0) {
return lastNode.v;
}
return null;
}
public K firstKey() {
if (root == null) {
return null;
}
AVLNode<K, V> cur = root;
while (cur.l != null) {
cur = cur.l;
}
return cur.k;
}
public K lastKey() {
if (root == null) {
return null;
}
AVLNode<K, V> cur = root;
while (cur.r != null) {
cur = cur.r;
}
return cur.k;
}
public K floorKey(K key) {
if (key == null) {
return null;
}
AVLNode<K, V> lastNoBigNode = findLastNoBigIndex(key);
return lastNoBigNode == null ? null : lastNoBigNode.k;
}
public K ceilingKey(K key) {
if (key == null) {
return null;
}
AVLNode<K, V> lastNoSmallNode = findLastNoSmallIndex(key);
return lastNoSmallNode == null ? null : lastNoSmallNode.k;
}
}
}