[数据结构与算法]LeetCode每日一题(All Possible Full Binary Trees)

Given an integer n, return a list of all possible full binary trees with n nodes. Each node of each tree in the answer must have Node.val == 0.

Each element of the answer is the root node of one possible tree. You may return the final list of trees in any order.

A full binary tree is a binary tree where each node has exactly 0 or 2 children.

Example 1:

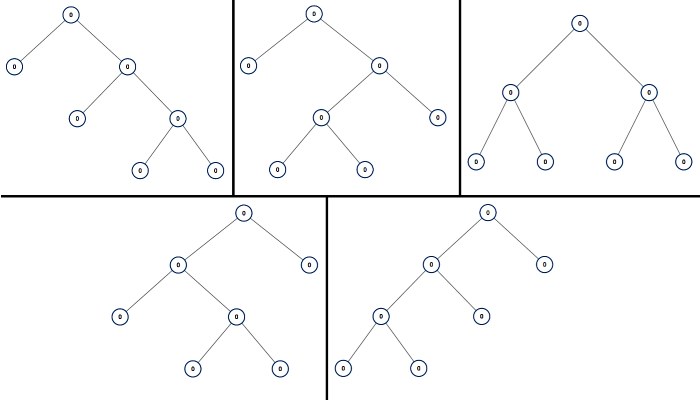
Input: n = 7
Output: [[0,0,0,null,null,0,0,null,null,0,0],[0,0,0,null,null,0,0,0,0],[0,0,0,0,0,0,0],[0,0,0,0,0,null,null,null,null,0,0],[0,0,0,0,0,null,null,0,0]]

Example 2:

Input: n = 3
Output: [[0,0,0]]

Constraints:

• 1 <= n <= 20

这题着实费了点功夫去想， 一开始还是想着用递归加遍历的方式来做， 但是因为是要生成完全二叉树， 所以比较复杂。后来看着图，突然想到，其实完全二叉树就是一个根节点和左右两个完全二叉树的组合， 这样我们从只包含一个节点的二叉树开始推， 推到 n 个节点的二叉树的所有排列就可以了。这里要注意一点的是，只有 n 为奇数的时候才能生成完全二叉树。

use std::cell::RefCell;
use std::collections::HashMap;
use std::rc::Rc;
impl Solution {
    fn clone(root: &Option<Rc<RefCell<TreeNode>>>) -> Option<Rc<RefCell<TreeNode>>> {
        if let Some(node) = root {
            let mut copy = TreeNode::new(node.borrow().val);
            copy.left = Solution::clone(&node.borrow().left);
            copy.right = Solution::clone(&node.borrow().right);
            return Some(Rc::new(RefCell::new(copy)));
        }
        None
    }
    pub fn all_possible_fbt(n: i32) -> Vec<Option<Rc<RefCell<TreeNode>>>> {
        if n % 2 == 0 {
            return vec![];
        }
        let mut m: HashMap<i32, Vec<Option<Rc<RefCell<TreeNode>>>>> =
            vec![(1, vec![Some(Rc::new(RefCell::new(TreeNode::new(0))))])]
                .into_iter()
                .collect();
        for i in (3..21).step_by(2) {
            if i > n {
                break;
            }

            let mut nodes = Vec::new();
            for l in (1..i).step_by(2) {
                let lefts = m.get(&l).unwrap().clone();
                let rights = m.get(&(i - 1 - l)).unwrap().clone();
                for left in &lefts {
                    for right in &rights {
                        nodes.push(Some(Rc::new(RefCell::new(TreeNode {
                            val: 0,
                            left: Solution::clone(left),
                            right: Solution::clone(right),
                        }))));
                    }
                }
            }
            m.insert(i, nodes);
        }
        m.get(&n).unwrap().clone()
    }
}