[数据结构与算法]比较排序：堆排序

堆

讲堆排序之前，我们先讲讲堆，下面是堆的的特点

• 堆总是一个完全二叉树
• 每个节点大于等于或者小于等于它的子节点

二叉树: 每个非叶子节点最多有两个分支节点
满二叉树: 每个非叶子节点都有两个子节点
除了最后一层，其上各层 (1～h-1) 的结点数都达到最大个数，并且最后一层所有的结点都连续集中在最左边，这就是完全二叉树
完全二叉树: 最后一层的最后一个节点的父节点不满足满二叉树之外，其它非叶子节点都满足满二叉树
满二叉树一定是完全二叉树，完全二叉树不一定是满二叉树

堆分为最小堆和最大堆

• 最大堆：是一个完全二叉树，父节点不小于子节点
• 最小堆：是一个完全二叉树，父节点不大于子节点

堆的特性：

• 堆的前一半是非叶子节点，后一般是叶子节点

下图是个最大堆，左子节点大于右子节点

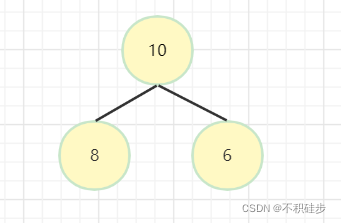
堆排序图解

堆排序如其它排序一样，给定一个数组 Integer[] array = {3,5,9,2,3,1,8};

• 数组中的元素是不符合堆的特性，所以首先要构建一个最大堆或者最小堆
• 构建一个堆的过程其实就是构建一颗完全二叉树，根据堆的特性，我们需要从最后一个分支节点开始向前堆化(堆调整)，至于为什么不向后，是因为后面都是叶子节点不需要在堆化了
• 堆排序：遍历构建的堆数组，从最后一个索引与第一个索引交换值，长度入当前堆化函数，做堆化，索引递减，直到索引为0结束循环

分支节点构建堆

思考：堆化其实就是当前节点与它们的孩子节点做比较，当前节点与孩子节点的最大值做交换形成最大堆或者最小堆，最后需要考虑堆化的临界条件

9是树的最后一个分支节点

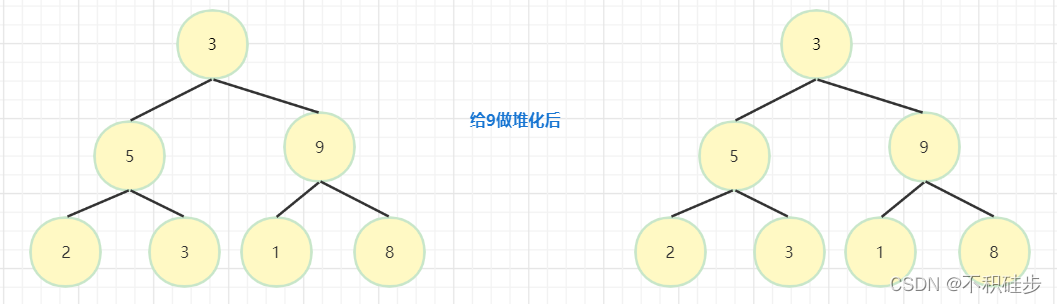
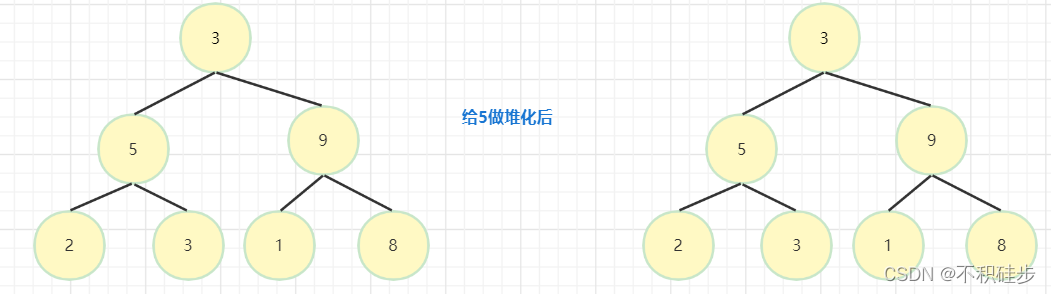
5做堆化

3做堆化

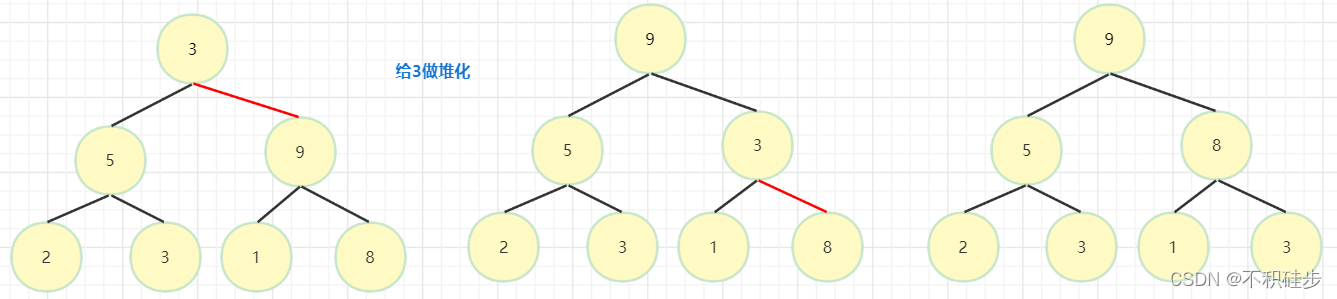
堆排序图解

遍历初始索引为6，索引6元素与第一个元素换值，传入元素在数组的索引为6，从0开始做堆化，大于等于6时结束

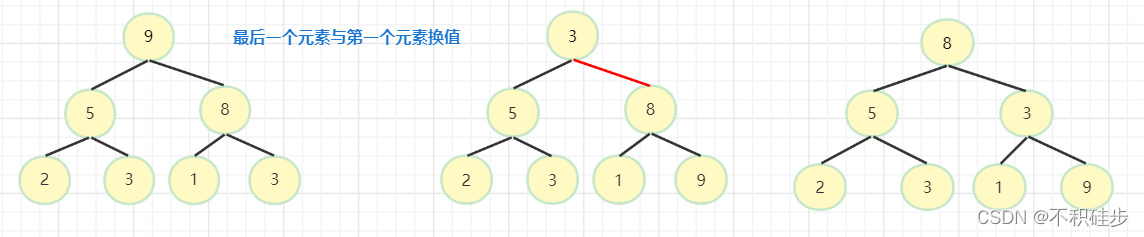
遍历到索引为5，索引5元素与第一个元素换值，传入元素在数组的索引为5，从0开始做堆化，大于等于5时结束

遍历到索引为4，索引4元素与第一个元素换值，传入元素在数组的索引为4，从0开始做堆化，大于等于4时结束

…

堆排序代码

java里面提供一个PriorityQueue类可以创建最大堆或者最小堆，想要快捷就可以调用它里面的sort方法

• 稳定性：不稳定
• 时间复杂度：O(nlogn)

import java.util.Arrays;

public class HeapSort {

    //交换值
    private void swap(Comparable[] array, int e1, int e2) {
        Comparable temp = array[e1];
        array[e1] = array[e2];
        array[e2] = temp;
    }

    //比较
    private boolean compare(Comparable e1, Comparable e2) {
        return e1.compareTo(e2) < 0;
    }

    //先构建堆
    private void buildHeap(Comparable[] array) {
        for (int i = array.length / 2 - 1; i >= 0; i--) {
            heapAdjust(array, i, array.length);
        }
        System.out.println("构建的堆:" + Arrays.toString(array));
    }


    public Comparable[] sort(Comparable[] array) {
        buildHeap(array);
        //遍历构建的堆数组,根据堆化完成排序
        //这个地方边界给>0,因为索引为0,长度为0,没必要做堆化
        for (int i = array.length - 1; i > 0; i--) {
            //这的操作有点向堆删除元素，进行下沉操作，但是下沉只能保证父节点不大于或者不小于子节点，并不能排序
            swap(array, i, 0);
            heapAdjust(array, 0, i);
            System.out.println(Arrays.toString(array));
        }
        return array;
    }

    //最主要的就是堆化的代码,需要琢磨清楚它的边界
    private void heapAdjust(Comparable[] array, int i, int len) {
        for (int index = 2 * i + 1; index < len; index = index * 2 + 1) {
            if (index + 1 < len && compare(array[index], array[index + 1])) {
                index = index + 1;
            }
            if (compare(array[i], array[index])) {
                swap(array, i, index);
                i = index;
            } else {
                break;
            }
        }
    }

}

public class HeapSortTest {
    public static void main(String[] args) {
        Integer[] array = {3, 5, 9, 2, 3, 1, 8};
        array = (Integer[]) new HeapSort().sort(array);
        System.out.println(Arrays.toString(array));
    }
}



构建的堆:[9, 5, 8, 2, 3, 1, 3]
[8, 5, 3, 2, 3, 1, 9]
[5, 3, 3, 2, 1, 8, 9]
[3, 2, 3, 1, 5, 8, 9]
[3, 2, 1, 3, 5, 8, 9]
[2, 1, 3, 3, 5, 8, 9]
[1, 2, 3, 3, 5, 8, 9]
[1, 2, 3, 3, 5, 8, 9]