1. 直线

题目

在这里插入图片描述

解析

因为要统计不同的直线，所以用直线的性质：斜率和截距来区分，并存放到集合容器里

直接使用k斜率去计算b截距，会产生精度爆炸，也就是说，编译器会自动省略掉后几位数字，导致题目错误，最常见的错误答案如下：

公式推导如下：

代码

points = [(x,y) for x in range(20) for y in range(21)]
docker = set()

for x in points:
    for y in points:
        x1,y1 = x[0],x[1]
        x2,y2 = y[0],y[1]
        if x1!=x2 and y1!=y2: # 同一竖线和横线不做计算
            k = (y2-y1)/(x2-x1)
            b = (x2*y1-x1*y2)/(x2-x1)
            docker.add((k,b))

print(len(docker) + 20 + 21)

2. 路径

题目

在这里插入图片描述

解析

融合了最短路径，最小公倍数和动态规划。
其中最小公倍数需要使用时间复杂度最低的，不能用while循环来找最小公倍数，亲测时间会很长。

最小公倍数数时间复杂度最低的模板：

# 最小公倍数模板(least common multiple)
def lcm(a,b):
    if a<b:
        a,b=b,a
    c,d=a,b
    while d!=0:
        c,d=d,c%d
    return (a*b)//c

关于动态规划的解析：
https://blog.csdn.net/lijiamingccc/article/details/123673506

这里动态规划的递推公式如下：
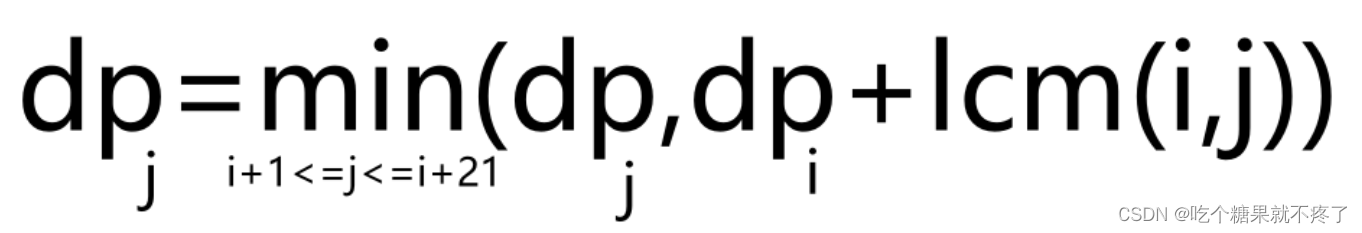
在这里插入图片描述
其中 dp[j] 是1到j位置的路径长度，dp[i]+lcm(i,j) 从第i个结点经过lcm(i,j) 的距离到达j位置的路径长度，两者取最小值

代码

# 最短路径(dp)
n=2021                          #结点数量
dp=[float('inf')]*(n+1)         #创建列表赋值为无穷大
dp[1]=0                         #结点1的长度初始化为0
for i in range(1,n+1):          #结点a：遍历结点1~n
    for j in range(i+1,i+22):   #结点b：遍历结点i+1~i+21
        if j>n:                 #j超出结点范围时
            break               #结束循环
        dp[j]=min(dp[j],dp[i]+lcm(i,j))#递推公式
print(dp[n])                    #输出结果：10266837

3. 双阶乘

题目

在这里插入图片描述

代码

送分题无解析

sum_ = 1
for i in range(1,2022,2):
    sum_ = (sum_*i) %100000

print(sum_)

在这里插入图片描述

4. 几个2020

题目

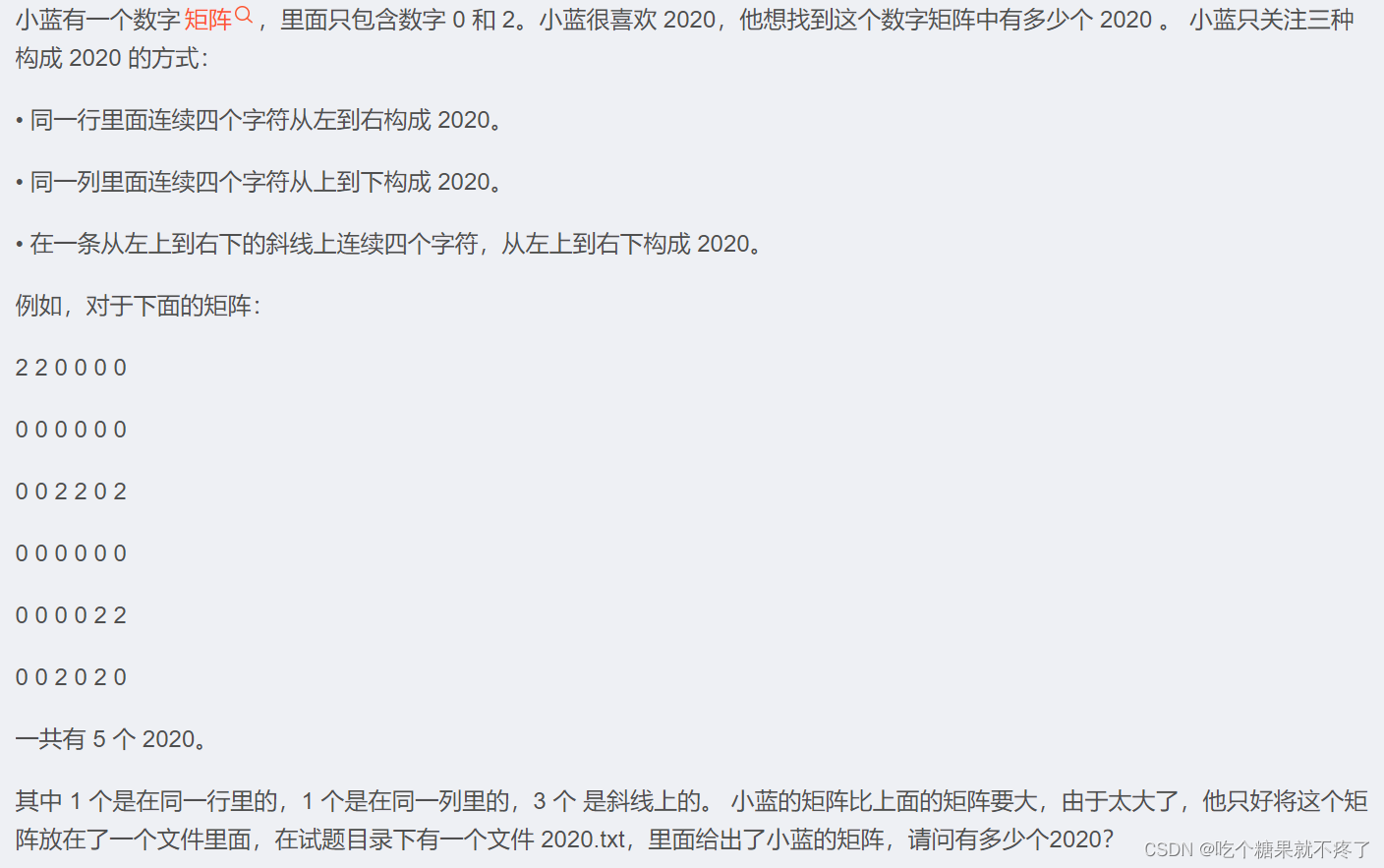
在这里插入图片描述
常见错误示例：

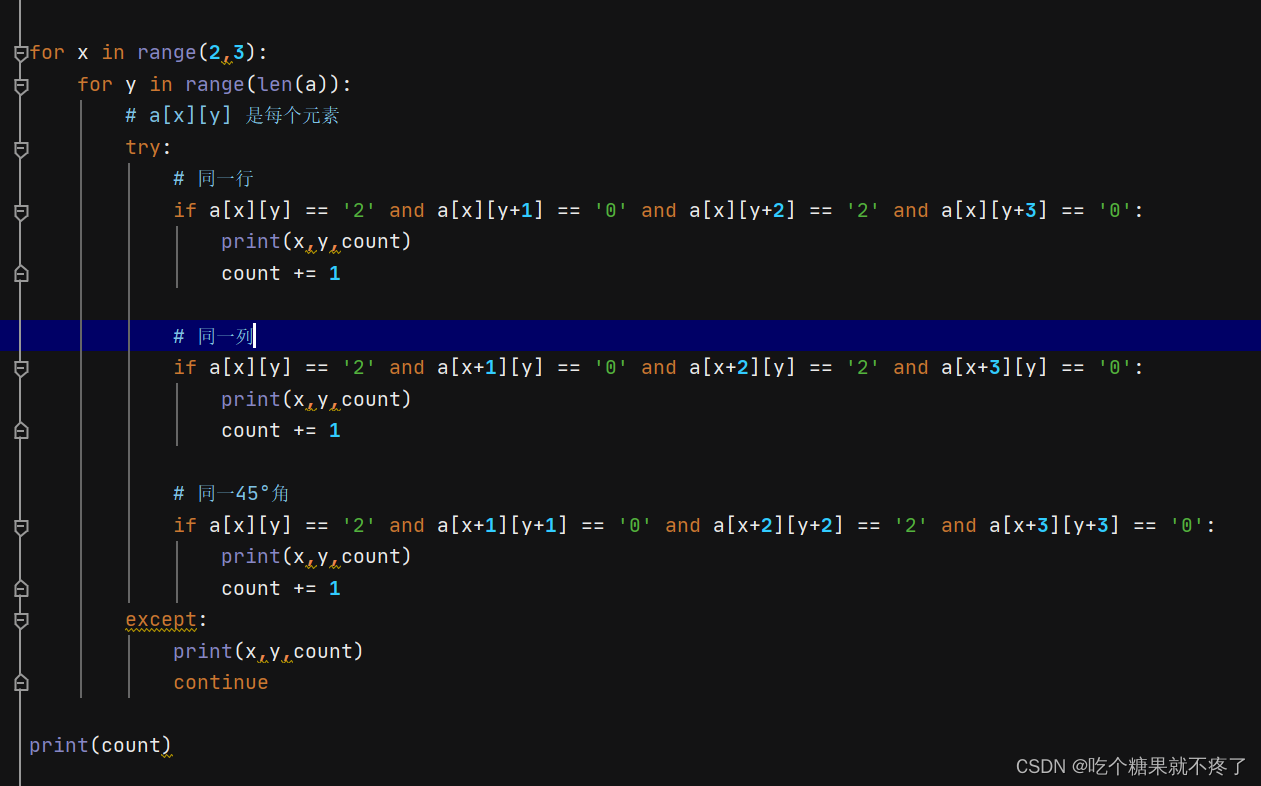
这里不正确的原因，主要是边界判断条件不一致，容易提前退出循环，导致统计不充分

代码

正确代码

#枚举-2020
a = [["2","2","0","0","0","0"],
    ["0","0","0","0","0","0"],
    ["0","0","2","2","0","2"],
    ["0","0","0","0","0","0"],
    ["0","0","0","0","2","2"],
    ["0","0","2","0","2","0"]]
cnt=0                   #计数器
n=len(a)                #长和宽一样长

for i in range(n):      #按行遍历
    for j in range(n-3):
        if a[i][j]=="2" and a[i][j+1]=="0" and a[i][j+2]=="2" and a[i][j+3]=="0":
            cnt+=1

for i in range(n-3):    #按列遍历
    for j in range(n):
        if a[i][j]=="2" and a[i+1][j]=="0" and a[i+2][j]=="2" and a[i+3][j]=="0":
            cnt+=1

for i in range(n-3):    #按对角线遍历
    for j in range(n-3):
        if a[i][j]=="2" and a[i+1][j+1]=="0" and a[i+2][j+2]=="2" and a[i+3][j+3]=="0":
            cnt+=1
            
print(cnt)              #输出结果：5