1、什么是字典树
如下图就是一颗字典树, 这是往树里插入字符串 he、she、hers、his、shy 生成的树
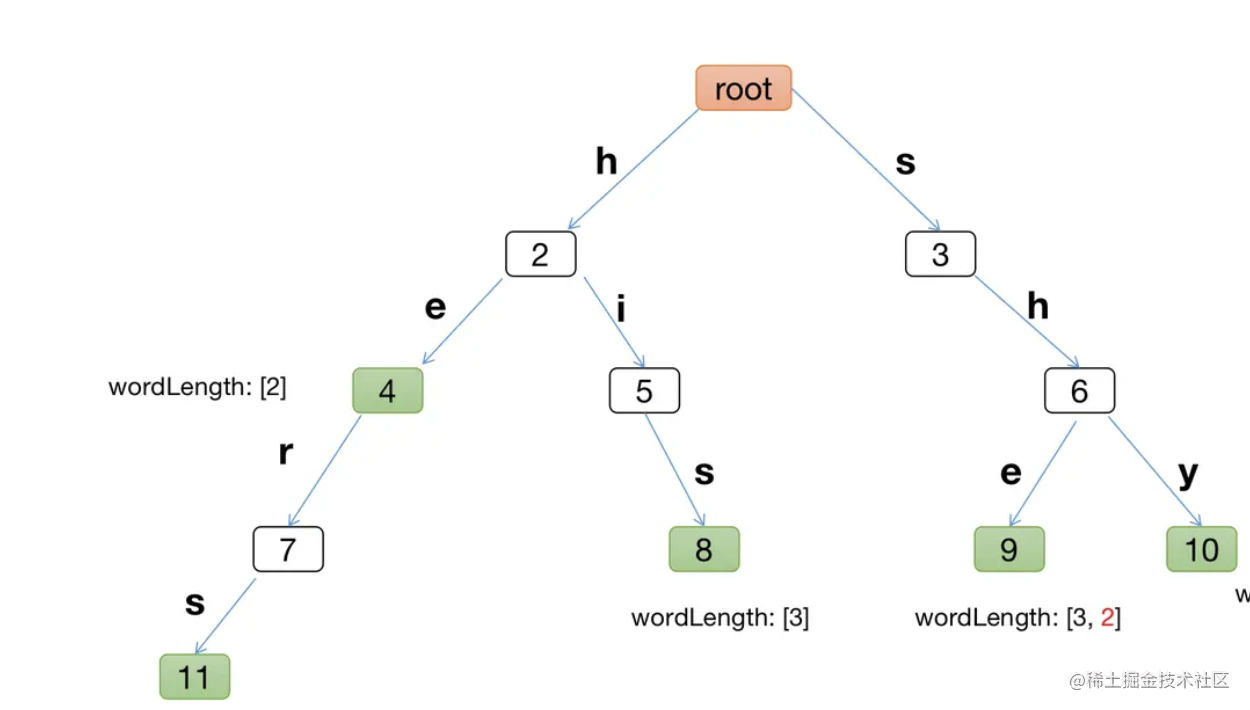
特点
-
字典树又名
前缀树和单词查找树, 每个字符串的公共前缀都将作为一个字符节点保存。 -
它本质是一颗多叉树, 除了根节点, 每个节点只存放一个字符, 从根节点到某一
绿色节点,路径上经过的字符连接起来,就是该节点对应的字符串。- 比如 从根节点root到 8号节点 经过的路径连接起来就是一个插入的字符串
his
- 比如 从根节点root到 8号节点 经过的路径连接起来就是一个插入的字符串
2、字典树能做什么
核心是空间换时间,优点是利用字符串的公共前缀来降低查询时间的开销以达到提高效率的目的,查询的时间复杂度仅与搜索的字符串的长度有关,即 时间复杂度为O(len), 而普通二分搜索树的时间复杂度为O(logN), 缺点是比较耗空间, 毕竟以前一个节点可以存放一整个字符串,现在只能存放一个字符, 虽然可以通过修改为压缩字典树, 但同时也增加了维护成本
常见应用场景
词频统计- 如果不需要用到字典树的其他特性,还是用哈希表好,毕竟时间复杂度接近O(1), 而且字典树比较耗空间
前缀匹配- 通讯录前缀匹配
- 浏览器搜索提示匹配,自动补全
字符串搜索- 在一个字符串集合, 判断是否存在某一个字符串
其他数据结构扩展- 如后缀树,压缩字典树、三分搜索树、AC自动机
3、代码实现
/**
* 字典树
* @author burukeyou
*/
public class Trie {
// 树节点
@Data
@EqualsAndHashCode
class Node {
//当前节点表示的字符
public Character name;
// 子节点列表 Map<子节点字符,子节点>
public TreeMap<Character,Node> next;
// 是否表示一个单词的结尾
public boolean isWordEnd;
// 前缀经过这个节点的字符的数量
public int prefixCount;
// 父节点
private Node parent;
public Node(boolean isWordEnd) {
this(null,isWordEnd,0);
}
public Node(Character name, boolean isWordEnd, int prefixCount) {
this.name = name;
this.isWordEnd = isWordEnd;
this.prefixCount = prefixCount;
this.next = new TreeMap<>();
}
public Node(Character name, boolean isWordEnd, int prefixCount, Node parent) {
this(name,isWordEnd,prefixCount);
this.parent = parent;
}
}
// 根节点
private Node root;
//字典树中单词的个数
private int size;
public Trie() {
this.root = new Node(false);
this.size = 0;
}
/**
* 添加单词word
- 先将字符串拆成每个字符, 然后每个字符作为一个节点依次从上往下插入即可。 生成的树的路径结构刚好就是字符串字符的顺序。
*/
public void add(String word){
//
Node cur = this.root;
for (char key : word.toCharArray()) {
//cur节点的子节点们不存在该字符,则直接插入该子节点即可
if(!cur.next.containsKey(key)){
cur.next.put(key,new Node(key,false,1,cur));
}else{
// 存在相同前缀, 前缀数量+1
cur.next.get(key).prefixCount++;
}
// 更新指针
cur = cur.next.get(key);
}
// 此时 cur指针指向一个单词的最后一个字符节点,如果这个节点还不是表示一个单词结尾,则标记它
if (!cur.isWordEnd){
cur.isWordEnd = true;
this.size++;
}
}
/**
* 删除单词
先向下搜索到此字符串的最后一个子节点。 如果字符串不存在则无需删除。 如果存在, 则看是不是
叶子节点, 如果不是叶子节点直接把节点的单词标记位清除即可。
如果是叶子节点, 则一直往上搜索是标记单词的节点 或者 是被使用过的节点就停止搜索(说明从该节点开始是无需删除的),
然后从直接删除该节点下的要被删除的子节点即可。
*/
public void remove(String word){
Node node = getPrefixLastNode(word);
if (node == null || !node.isWordEnd){
System.out.println("单词不存在");
return;
}
// 如果不是叶子节点直接把单词标记去掉即可
if (!node.next.isEmpty()){
node.isWordEnd = false;
}else{
// 往上找到是标记单词的 或者 被使用过的节点 就停止
Node pre = node; //指向需要被删除的子树的第一个节点
node = node.parent; // 当前迭代指针
while (node != null && !node.isWordEnd && node.prefixCount <= 1){
pre = node;
node = node.parent;
}
// 删除节点node的子节点pre.name
if (node != null){
node.next.remove(pre.name);
}
}
// 更新 从 root -> node路径上所有节点的 prefixCount 减1
while(node != null){
node.prefixCount--;
node = node.parent;
}
}
/**
* 广度遍历
*/
public void bfsTraverse() {
Queue<Node> queue = new ArrayDeque<>();
queue.offer(this.root);
// 上一层的最后一个节点
Node preLayerLastNode = this.root;
// 本层最后一个节点
Node curLayerLastNode = this.root;
int curLayer = 0; // 当前层数
while(!queue.isEmpty()){
Node tmp = queue.remove();
if (curLayer != 0){
System.out.print(tmp.name +"("+ tmp.prefixCount+"-" + tmp.isWordEnd + ")" + "\t");
}
TreeMap<Character, Node> treeMap = tmp.next;
if (treeMap != null && !treeMap.isEmpty()){
List<Node> arrayList = new ArrayList<>(treeMap.values());
queue.addAll(arrayList);
if (!arrayList.isEmpty()){
curLayerLastNode = arrayList.get(arrayList.size()-1);
}
}
//遍历到每一层的末尾就进行换行
if (preLayerLastNode.equals(tmp)){
curLayer++;
preLayerLastNode = curLayerLastNode;
System.out.print("\n" + curLayer + "| ");
}
}
}
/**
* 查询单词word是否在Trie中
按照word每个字符顺序向下搜索即可
*/
public boolean contains(String word) {
Node node = getPrefixLastNode(word);
return node != null && node.isWordEnd;
}
/**
* 查询是否在Trie中有单词以prefix为前缀
* @param prefix 前缀
按照prefix每个字符顺序向下搜索即可
*/
public boolean hasPrefix(String prefix){
return getPrefixLastNode(prefix) != null;
}
/**
* 是否包含某个模式的单词。 如 a..b. .可代表任意单词
* 见: leetcode: 211. 添加与搜索单词
*/
public boolean containPatternWord(String word) {
return match(root, word, 0);
}
// 从 Node 开始搜索 单词word的[index, 结尾]部分
private boolean match(Node node, String word, int index){
if(index == word.length())
return node.isWordEnd;
char c = word.charAt(index);
if(c != '.'){
if(node.next.get(c) == null)
return false;
return match(node.next.get(c), word, index + 1);
}
else{
for(char nextChar: node.next.keySet())
if(match(node.next.get(nextChar), word, index + 1))
return true;
return false;
}
}
/**
* 查找前缀为prefix的所有单词
*/
public List<String> searchPrefix(String prefix) {
Node cur = getPrefixLastNode(prefix);
// 从这个节点往下深搜
List<String> paths = new ArrayList<>();
dfsSearchAllPath(cur,paths,prefix);
return paths;
}
/**
* 从节点开始深搜每条路径
* @param node 起始节点
* @param paths 保存结果的路径
* @param curPath 当前搜索的路径
*/
private void dfsSearchAllPath(Node node, List<String> paths, String curPath) {
if (node == null || node.next.isEmpty()) {
paths.add(curPath);
return;
}
for (Node child : node.next.values()) {
dfsSearchAllPath(child,paths,curPath + child.name);
}
}
/**
* 词频统计
* 获取前缀prefix的数量
*/
public int getPrefixCount(String prefix){
Node node = getPrefixLastNode(prefix);
return node != null ? node.prefixCount : 0;
}
// 获取前缀表示的最后一个节点
private Node getPrefixLastNode(String prefix){
// 往下搜每个字符节点,能搜到结尾即代表存在并返回
Node cur = root;
for (char key : prefix.toCharArray()) {
if(!cur.next.containsKey(key))
return null;
cur = cur.next.get(key);
}
return cur;
}
/**
* 搜索模式串
*/
public List<String> search(String patternWord){
// 去除空格特殊字符之类
patternWord = patternWord
.replaceAll("\s*","")
.replaceAll("((?=[\x21-\x7e]+)[^A-Za-z0-9])[\x21-\x7e]+[^A-Za-z0-9]","");
List<String> paths = new ArrayList<>();
dfsSearchAllPatternPath(root,patternWord,0,paths,"");
return paths;
}
/**
* 深搜每条路径, 如果路径经过 word就保存起来
* @param node 当前处理的节点
* @param patternWord 搜索的模式串
* @param index 当前搜索的模式串中的字符的下标
* @param paths 保存结果
* @param curPath 当前搜索的路径
*/
private void dfsSearchAllPatternPath(Node node, String patternWord, int index, List<String> paths, String curPath){
if (node == null) {
return;
}
if (node.isWordEnd && patternWord.length() == index){
paths.add(curPath);
}
for (Node child : node.next.values()) {
int tmpIndex = index;
if (tmpIndex < patternWord.length() && patternWord.charAt(tmpIndex) == child.name){
tmpIndex++;
}
dfsSearchAllPatternPath(child,patternWord,tmpIndex,paths,curPath + child.name);
}
}
}
4、快速开始
4.1 生成字典树
Trie trie = new Trie();
// 添加词库
trie.add("这个杀手冷静");
trie.add("冷静的杀手");
trie.add("杀手冷静");
trie.add("杀手百度云");
trie.add("杀手冷静点说的什么");
trie.add("杀手冷静成本");
trie.add("这个杀手不太冷静完整版在线观看");
trie.add("这个杀手不太冷静电影");
trie.add("这个杀手不太冷静是什么意思");
trie.add("这个杀手不太冷静电影");
trie.add("这个杀手不太冷静迅雷下载");
trie.add("这个杀手不太冷静百度网盘");
trie.add("豆瓣这个杀手不太冷静");
trie.add("这个杀手不太冷静");
trie.add("这个杀手不太冷静");
trie.add("这个诅咒太棒了");
trie.add("这个杀手不太冷静");
trie.add("极其安静的顶尖杀手");
trie.add("这个杀手不冷漠");
trie.add("最冷酷的杀手");
trie.add("一个极其安静的顶尖杀手");
4.2 树广度遍历
也叫层序遍历, 原理就是通过队列去维护遍历的顺序, 如遍历第一层后, 下一次要遍历的就是第二层, 所以把第二层的元素都添加到队列。
trie.bfsTraverse();
结果如下:
- 冷(1-false)表示一个节点, 存放的字符是冷, 前缀词频是1, fasle表示不是一个单词的结尾
1| 一(1-false) 冷(1-false) 最(1-false) 杀(4-false) 极(1-false) 豆(1-false) 这(12-false)
2| 个(1-false) 静(1-false) 冷(1-false) 手(4-false) 其(1-false) 瓣(1-false) 个(12-false)
3| 极(1-false) 的(1-false) 酷(1-false) 冷(3-false) 百(1-false) 安(1-false) 这(1-false) 杀(11-false) 诅(1-false)
4| 其(1-false) 杀(1-false) 的(1-false) 静(3-true) 度(1-false) 静(1-false) 个(1-false) 手(11-false) 咒(1-false)
5| 安(1-false) 手(1-true) 杀(1-false) 成(1-false) 点(1-false) 云(1-true) 的(1-false) 杀(1-false) 不(10-false) 冷(1-false) 太(1-false)
6| 静(1-false) 手(1-true) 本(1-true) 说(1-false) 顶(1-false) 手(1-false) 冷(1-false) 太(9-false) 静(1-true) 棒(1-false)
7| 的(1-false) 的(1-false) 尖(1-false) 不(1-false) 漠(1-true) 冷(9-false) 了(1-true)
8| 顶(1-false) 什(1-false) 杀(1-false) 太(1-false) 静(9-true)
9| 尖(1-false) 么(1-true) 手(1-true) 冷(1-false) 完(1-false) 是(1-false) 电(2-false) 百(1-false) 迅(1-false)
10| 杀(1-false) 静(1-true) 整(1-false) 什(1-false) 影(2-true) 度(1-false) 雷(1-false)
11| 手(1-true) 版(1-false) 么(1-false) 网(1-false) 下(1-false)
12| 在(1-false) 意(1-false) 盘(1-true) 载(1-true)
13| 线(1-false) 思(1-true)
14| 观(1-false)
15| 看(1-true)
16|
4.3 搜索前缀匹配

如上图通过我们输入前缀这个,就会提示后面可以输入的所有单词如, 这时可以用前缀匹配, 先搜索到前缀的最后一个节点, 然后从该节点开始DFS深搜每条路径,找到所有符合的单词
// 搜索前缀为 “这个”的所有单词
List<String> searchPrefix = trie.searchPrefix("这个");
for (String prefix : searchPrefix) {
System.out.println(prefix);
}
结果:
这个杀手不冷漠
这个杀手不太冷静完整版在线观看
这个杀手不太冷静是什么意思
这个杀手不太冷静电影
这个杀手不太冷静百度网盘
这个杀手不太冷静迅雷下载
这个杀手冷静
这个诅咒太棒了
4.4 搜索单词提示
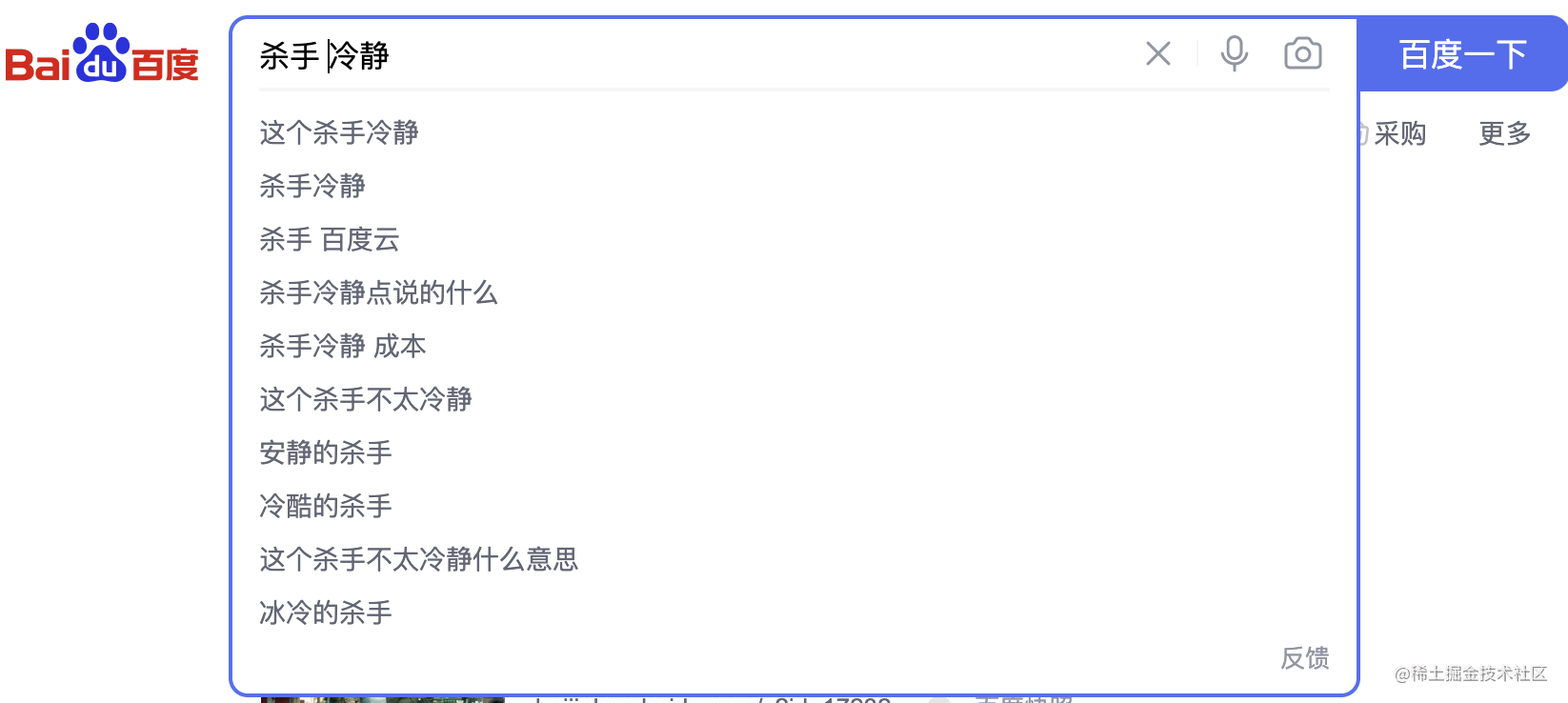
如上图, 我们搜索 两个关键字 杀手冷静, 将包含这四个字符的并且顺序一致的所有单词搜索出来。 原理也是用DFS深搜每条路径, 但是只把包含搜索字符的路径保存下来
// 搜索单词杀手冷静
List<String> tmpList = trie.search("杀手冷静");
for (String tmp : tmpList) {
System.out.println(tmp);
}
结果:
杀手冷静
杀手冷静成本
杀手冷静点说的什么
豆瓣这个杀手不太冷静
这个杀手不太冷静
这个杀手不太冷静完整版在线观看
这个杀手不太冷静是什么意思
这个杀手不太冷静电影
这个杀手不太冷静百度网盘
这个杀手不太冷静迅雷下载
这个杀手冷静
4.5 前缀词频统计
由于在添加的时候就维护了前缀的数量, 所以搜索到单词最后一个节点后直接获取词频即可。
int prefixCount = trie.getPrefixCount("");
List<String> tmp = trie.search("杀手冷静");
for (String name : tmp) {
int prefixCount = trie.getPrefixCount(name);
System.out.println("关键字: "+ name + ", 前缀搜索次数: " + prefixCount);
}
结果:
关键字: 杀手冷静, 前缀搜索次数: 3
关键字: 杀手冷静成本, 前缀搜索次数: 1
关键字: 杀手冷静点说的什么, 前缀搜索次数: 1
关键字: 豆瓣这个杀手不太冷静, 前缀搜索次数: 1
关键字: 这个杀手不太冷静, 前缀搜索次数: 9
关键字: 这个杀手不太冷静完整版在线观看, 前缀搜索次数: 1
关键字: 这个杀手不太冷静是什么意思, 前缀搜索次数: 1
关键字: 这个杀手不太冷静电影, 前缀搜索次数: 2
关键字: 这个杀手不太冷静百度网盘, 前缀搜索次数: 1
关键字: 这个杀手不太冷静迅雷下载, 前缀搜索次数: 1
关键字: 这个杀手冷静, 前缀搜索次数: 1