[数据结构与算法]蓝桥杯算法提高-能量项链（区间DP）

?

?解题思路：一开始就理解错题意了，以为是从n个珠子中随机选一个，然后按顺时针挨个合并最后取个最大值就完了，然后提交答案WA在了第50个样例，一开始以为模拟过程模拟的不对，后来发现没有问题，越想越感觉没毛病，没招了只好偷偷瞄了一眼答案，发现理解错题意了QAQ，理解能力实在是太差了，之间重要的比赛在这上面吃了不少亏了，还是改不了，果然是自作孽不可活。

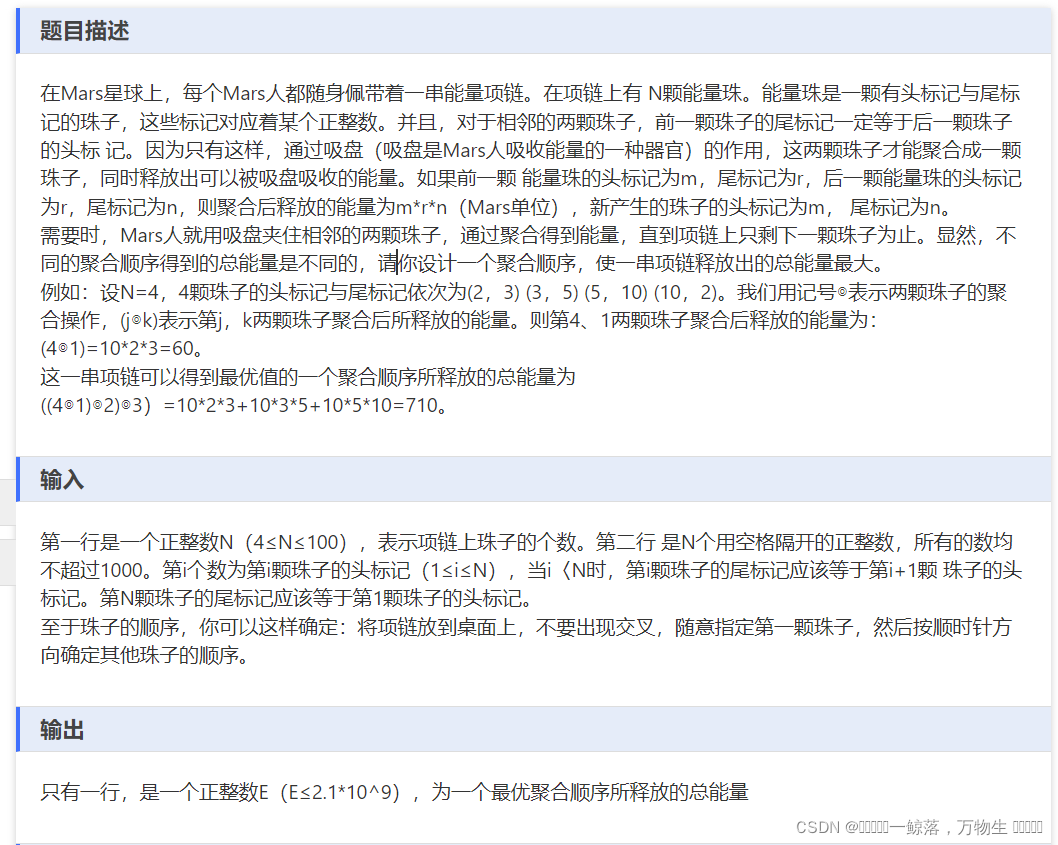
回到正题，终于了解了正确题意的我，不由自主的被偷瞄到的答案带到了区间DP上来，额，还是先来说下题意把，给我们了n个数，第i个数表示第i个珠子的头表示是ai，它的尾节点是它的后一个数（第i+1个数），我们对每两个珠子可以进行合并操作，合并后会释放一定的能量，释放的能量=前一个珠子的头标记*后一个珠子的头标记*后一个珠子的尾标记，每次只能是按顺时针进行合并，就是相邻的2个珠子，左边的和右边的合并，合并后2个珠子变成一个珠子，谁先合并没有要求，注意这串珠子是围成一个圈的，题目要我们输出释放能量的最大值。想到这里不难看出这是一个非常典型的区间DP问题，它和环形石子合并问题几乎就是一模一样的，思路比较简单看代码就能看明白，就是在枚举中间变量k的时候需要思考一下从那一段来枚举。

代码如下：

#include <iostream>
#include <cstring>
#include <cstdio>
#include <algorithm>
using namespace std;
int a[310];
int dp[110][110];
int main()
{
	int n;	
	cin>>n;
	for(int i=1;i<=n;i++)
	cin>>a[i];
	for(int i=n+1;i<=n+n;i++)
	a[i]=a[i-n];
	int maxv=-0x3f3f3f3f;
    for(int len=2;len<=n;len++)
    {
    	for(int i=1;i+len-1<=n+n;i++)
    	{
    		int j=i+len-1;
    		for(int k=i;k<j;k++)
    		dp[i][j]=max(dp[i][j],dp[i][k]+dp[k+1][j]+a[i]*a[k+1]*a[j+1]);
		}
	}
	for(int i=1;i<=n;i++)
	maxv=max(maxv,dp[i][i+n-1]);
	cout<<maxv<<endl;
	return 0;
 }