[数据结构与算法]欧拉降幂（串联欧拉函数，逆元等等）

欧拉函数？

含义

欧拉函数φ(n) 代表的是小于n的数中，与n互质的数（gcd=1)的个数。

如何求解

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long ll;
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        ll x;
        cin>>x;
        ll phi=x;
        for(ll i=2;i*i<=x;i++)
        {
            if(x%i==0)
            {
                phi=phi*(i-1)/i;
                while(x%i==0)
                    x/=i;
            }
        }
        if(x>1) phi=phi*(x-1)/x; //别忘了
        cout<<phi<<endl;
    }
    return 0;
}

乘法逆元

首先，数学上的乘法逆元就是指直观的倒数，即 [公式] 的逆元是 [公式]，也即与 [公式] 相乘得 1 的数。[公式]，则[公式]是[公式]的乘法逆元。

这里我们讨论关于取模运算的乘法逆元，即对于整数 [公式]，与 [公式] 互质的数 [公式] 作为模数，当整数 [公式] 满足 [公式] 时，称 [公式] 为 [公式] 关于模 [公式] 的逆元，代码表示就是a * x % b == 1。

费马小定理

若存在整数 a , p 且gcd(a,p)=1,即二者互为质数，则有a^(p-1)≡ 1(mod p)。(这里的 ≡ 指的是恒等于，a^(p-1)≡ 1(mod p)是指a的p-1次幂取模与1取模恒等)

欧拉降幂

公式：

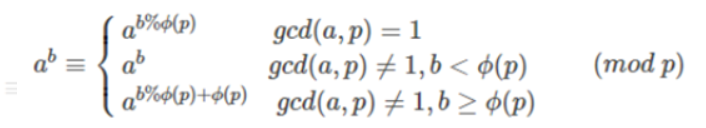
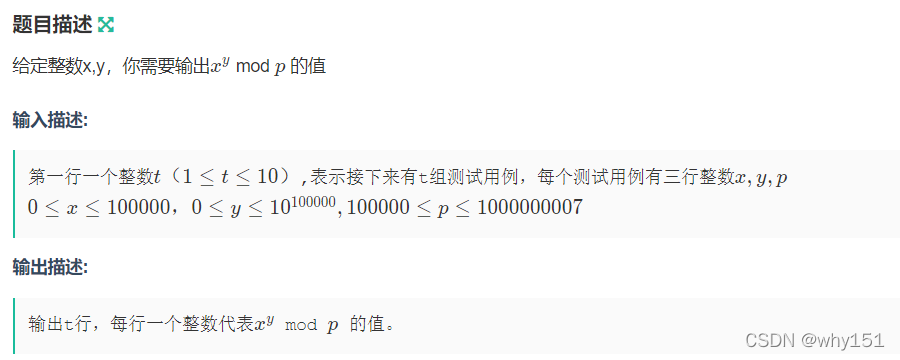
例题：

https://ac.nowcoder.com/acm/contest/30825/J

#include<iostream>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
bool book;
ll find_phi(ll x)
{
    ll ans=x;
    for(ll i=2;i*i<=x;i++)
    {
        if(x%i==0)
        {
            ans=ans*(i-1)/i;
            while(x%i==0) x/=i;
        }
    }
    if(x>1) ans=ans*(x-1)/x;
    return ans;
}
ll find_yy(string y,ll phi)
{
    ll now=0;
    for(int i=0;i<y.size();i++)
    {
        now=now*10+y[i]-'0';
        if(now>=phi)
            now%=phi,book=1;
    }
    return now;
}
ll qpow(ll x,ll y,ll p)
{
    ll ans=1;
    while(y)
    {
        if(y&1) ans=(ans*x)%p;
        x=(x*x)%p;
        y>>=1;
    }
    return ans;
}
int main()
{
    int t;
    cin>>t;
    while(t--)
    {
        book=0;
        string y;
        ll x,p;
        cin>>x>>y>>p;
        ll phi=find_phi(p);
        ll yy=find_yy(y,phi);
        if(__gcd(x,p)!=1&&book) yy+=phi;
        ll ans=qpow(x,yy,p);
        cout<<ans<<endl;
    }
    return 0;
}