临近蓝桥杯需要练习真题以提高自身算法基本功,当然说实话时间也是没多少,只能抽时间来做并且做个讲解了。这是2021年的蓝桥杯试题解析点击此处
分析这2份真题还是能发现出很多共性的,首先是基本题目给分到位,接近一半的题目都可以通过暴力枚举来得出答案,然而这其中还是有很多小细节的。不过可以清晰地发现蓝桥杯题目确实一年比一年难了,所以也只能提高自身技术才会游刃有余。
每一个思路都能在20年和21年找到类似,这里做个大致汇总:
1.gcd辗转相除法 :20年既约分数 21年路径
2.查找数字包含的个数 :20年门牌制作 21年卡片
3.set去重判断交点 : 20年平面切分 21年直线
4.针对已知矩阵找规律打表 : 20年蛇形填数 21年杨辉三角形
本次填空题5道4道完全可以做出来,没有一丝难度。大题除最后一题难度比较高以外其他都比较正常,都是常见题目,下面通过我一步步讲解来吧,不过最后一题我暂时没有太好的思路。
注意,20年和21的算法题非常类似,所以抓住真题练习算法绝对有收获!
本文难题参考博客(最后一题):
参考博客1
门牌制作(5分)

总体思路就是拆分数字,思路和21年蓝桥杯题目2类似,应该重点关注。只要从1-2000找出包含2,然后sum++即可,不过友情提醒,需要在每次循环的时候保存到temp中,不然循环会一直进行哦!
#include <iostream>
using namespace std;
int main(){
int sum=0,temp;
for(int i=1;i<=2020;i++){
int ti=i;
while(ti){
temp=ti%10;
if(temp==2){
sum++;
}
ti/=10;
}
}
cout<<sum<<endl;
return 0;
}
既约分数(5分)

不用多说了吧,去年蓝桥杯图论也考了相应的知识点,就是gcd,寻找公因数与公倍数,使用辗转相除法,重点算法。
#include <iostream>
using namespace std;
int gcd(int a,int b){
return a%b==0?b:gcd(b,a%b);
}
int main(){
int sum=0;
for(int i=1;i<=2020;i++){
for(int j=1;j<=2020;j++){
int mi=max(i,j);
int mj=min(i,j);
if(gcd(i,j)==1){
sum++;
}
}
}
cout<<sum<<endl;
return 0;
}
蛇形填数(10分)

此题我是思考许久,思路就是先打表然后找出在表中的数字,但是如何对表进行填数,这就很关键了。仔细观察这个矩阵,很容易发现,每行与每行之间存在着关系例如这里选取一部分进行观察。
我们把矩阵拆分成这样来看,很清晰的发现以下规律:
1.偶数列的数字从小到大每次加1;
2.奇数列的数字从大到小每次减1;
通过以上发现便很清晰的找到了关系,也就是说我们算出第一行其余也都出来了。所以第一行又有什么规律呢?
将每2个数分成1组,即(1,2),(6,7)(15,16),也就是说只要找到奇数项偶数项只要+1即可,而奇数项规律:以1,6,15分析,差值为5,9…猜想差值按照等差数列d=4进行排列。
至此规律已全部找出,下面就是解题过程:
1.先找出按照公式找出第1行数据,2.按照j>=i的规律打印此矩阵。3.然后把此矩阵赋给另一个矩阵B,遇到0就跳过,这样就确保了正确,以下是代码过程!
当然了这个题目还是有简单的方法,直接观察:可以斜着看,第一条斜线是:1;第二条是:2, 3;第20行第20列的数在第39条斜线上的中点位置。所以该数是:1+2+…+38+20=761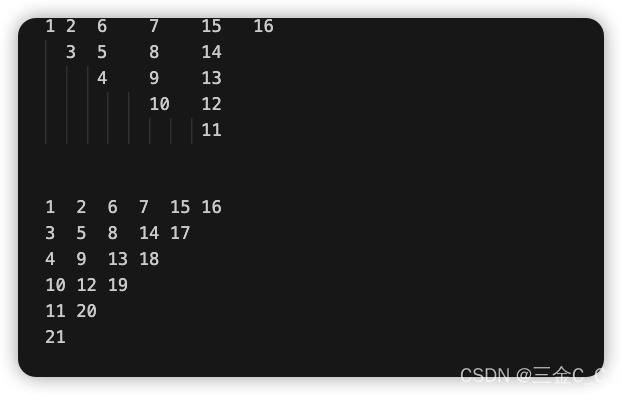
#include <iostream>
#include <cstring>
using namespace std;
long long a[90][90];
long long b[90][90];
int main(){
int di=4;
memset(a,0,sizeof(a));
a[1][1]=1;
a[1][2]=2;
for(int i=3;i<=90;i++){
if(i%2!=0){
a[1][i]=a[1][i-1]+di;
di+=4;
}else{
a[1][i]=a[1][i-1]+1;
}
}
for(int i=2;i<=90;i++){
for(int j=i;j<=90;j++){
if(j%2==0){
a[i][j]=a[i-1][j]+1;
}else{
a[i][j]=a[i-1][j]-1;
}
}
}
for(int i=1;i<=90;i++){
int temp=1;
for(int j=1;j<=90;j++){
if(a[i][j]>0){
b[i][temp]=a[i][j];
temp++;
}
}
}
cout<<b[20][20]<<endl;
return 0;
}
跑步锻炼(10分)

简单的日期题,不过使用c++要自己写出代码实在是麻烦了,不过可以使用python或者java中的时间来解决。
#include <iostream>
using namespace std;
int year,month,day;
int mon[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
long long csum=0;
bool cmp_year(int year){
return (year%4==0&&year%100!=0)||(year%400==0)?true:false;
}
int main(){
cin>>year>>month>>day;
int week=6;
for(int i=2000;i<=year;i++){
mon[2]=28;
if(cmp_year(i)) {++mon[2];}
for(int j=1;j<=12;j++){
for(int k=1;k<=mon[j];k++){
++csum;
if(k==1||week%7==1) {++csum;}
++week;
if(i==year&&j==month&&k==day) goto here;
}
}
}
here:
cout<<csum<<endl;
return 0;
}
下面附个python代码轻松解决
import datetime
begin = datetime.date(2000, 1, 1) # datetime.date(year, month, day)
# print(begin) # 2000-01-01
end = datetime.date(2020, 10, 2)
# print(end)# 2020-10-02
count = 0
while begin != end:
if begin.day == 1 or begin.weekday() == 0: # date.weekday()返回一个整数代表星期几,星期一为0,星期天为6。
count += 2
else:
count += 1
begin += datetime.timedelta(days=1) # datetime.timedelta:表示两个 date 对象或 time 对象,或者 datetime 对象之间的时间间隔,精确到微秒
print(count)
七段码(15分)

这个题目呢我觉得考场有时间可以强行暴力枚举一下,答案也不多。这个题目我一开始以为就是从这7个里面选1,2,…7个的情况,然而并非如此简单,因为他需要连成一片。一想到这里,就明白这个题目意思了。问连通性的情况,那必定有图论的dfs来做了。
思路:首先定义1-7序号的完全无向图,将边赋值为1。重点是每次的循环与dfs,具体的代码如下,学过dfs的同学比较好理解,考场这个题目没时间也不介意去写了。
#include<iostream>
using namespace std;
int d[8][8]={0};
int dp[8],cnt=-1;
int dfs2(int i,int p[]){
int sum=0;
for(int j=1;j<8;j++)
if(d[i][j]==1&&p[j]==0&&dp[j]==1){
sum+=j;
p[j]=1;
sum+=dfs2(j,p);
}
return sum;
}
int dfs1(){
int p[8]={0};
for(int i=1;i<8;i++)
if(dp[i]!=0){
p[i]=1;
return i+dfs2(i,p);
}
}
void csh(){
d[1][2]=d[2][1]=1;
d[1][7]=d[7][1]=1;
d[2][3]=d[3][2]=1;
d[2][4]=d[4][2]=1;
d[3][5]=d[5][3]=1;
d[3][4]=d[4][3]=1;
d[5][6]=d[6][5]=1;
d[6][4]=d[4][6]=1;
d[6][7]=d[7][6]=1;
d[4][7]=d[7][4]=1;
}
int fax(int i){
if(i==8)
{
int sum=0;
for(int j=1;j<8;j++)
sum+=dp[j]*j;
if(sum==dfs1())
cnt++;
}
else
{
dp[i]=0;
fax(i+1);
dp[i]=1;
fax(i+1);
}
}
int main()
{
csh();
fax(1);
cout<<cnt<<endl;
}
成绩统计 (15分)

额,这个题不就是明摆着送分吗?但是也要注意四舍五入的情况哦,这个还是有点讲究的,那就使用一下round函数啦,当然如果考场想不起来了,那就自己写个函数吧,这个还是比较简答的,思路呢就是先就是对这个数+0.5然后强制成Int就成了。
#include <iostream>
#include <cmath>
using namespace std;
int n;
int main(){
cin>>n;
int m=0,t=0;
for(int i=1;i<=n;i++){
int x;
cin>>x;
if(x>=60)m++;
if(x>=85) t++;
}
double d=m*100*1.0/n;
double b=t*100*1.0/n;
cout<<round(d)<<"%"<<endl<<round(b)<<"%"<<endl;
return 0;
}
回文日期(20分)

这个题目又是回文,看来回文数是重点啊,这里面需要注意这几个方面,第一,是回文的判断,一般我就是使用string中的reverse函数了,不过这个遇到大的数字肯定会TLE,这次也。还有一种就是对数字来判断回文,主要思路就是使用栈,不过我没有进行尝试,因为有现成的还是使用现成的吧。当然了还有这个输出的日期是否符合题意,这个也非常重要,所以又要写个判断时间的函数了。
以下是通过80%样例的代码,还有20%是因为超时了,不过答案也可以算出来,可以值得优化。
#include <iostream>
#include <string>
#include <cstring>
#include <algorithm>
#include <sstream>
using namespace std;
int data;
int mon[13]={0,31,28,31,30,31,30,31,31,30,31,30,31};
bool fun(int n){
string s="";
while(n){
int temp=n%10;
s+=temp-'0';
n/=10;
}
string m=s;
reverse(s.begin(),s.end());
return m==s?true:false;
}
bool sfun(int n){
string s="";
while(n){
int temp=n%10;
s+=temp-'0';
n/=10;
}
string m=s;
reverse(s.begin(),s.end());
if(s!=m) return false;
if(s[2]!=s[0]) return false;
if(s[3]!=s[1]) return false;
if(s[4]!=s[1]) return false;
if(s[5]!=s[0]) return false;
if(s[6]!=s[1]) return false;
if(s[7]!=s[0]) return false;
return true;
}
bool year(int n){
int mday=n%100;
int mmon=(n%10000-mday)/100;
int myea=(n-n%10000)/10000;
if((myea%4==0&&myea%100!=0)||(myea%400==0)) mon[2]++;
if(mmon>12) return false;
if(mday>mon[mmon]) return false;
return true;
}
int main(){
cin>>data;
int temp;
for(int i=data+1;;i++){
if(fun(i)){
if(year(i)){
cout<<i<<endl;
temp=i;
break;
}
}
}
for(int i=temp;;i++){
if(sfun(i)){
if(year(i)){
cout<<i<<endl;
break;
}
}
}
return 0;
}
子串分值和(20分)

这个题目我自己想的就是简单的暴力枚举,只能通过40%样例,思路就是使用set去重,不过这个时间复杂度也比较高,需要优化。
#include <iostream>
#include <set>
using namespace std;
set<char> m;
int sum=0;
int fun(string s){
m.clear();
for(int i=0;i<s.length();i++){
m.insert(s[i]);
}
return m.size();
}
int main(){
string str;
cin>>str;
for(int i=0;i<str.length();i++){
for(int j=0;j<str.length()-i;j++){
sum+=fun(str.substr(i,j+1));
}
}
cout<<sum<<endl;
return 0;
}
但是这个题有个绝杀思路,采用的是贡献值方法,代码如下:
通过100%样例
#include <iostream>
using namespace std;
int last[30];
long long ans = 0;
int main() {
string s;
cin >> s;
int len = s.length();
s = '0' + s; //下标从1开始
for (int i = 1; i <= len; i++) {
ans += (long long)(len - i + 1) * (i - last[s[i]-'a']);
last[s[i]-'a'] = i;
}
cout << ans;
return 0;
}
平面切分(25分)

这个题目乍一看很像高中时期做的题目,当时我记得我做的题目大概意思就是说,有N条直线如何划分最大空间。当时我清楚记得这个规律应为f(n)=f(n-1)+n,计算可得f(n)=n(n+1)/2+1。
那么这个思路又是怎么来的,这个就是猜的,通过数学归纳法总结的。但是我忽然也发现此题的规律,
首先这个题目先找出交点,还是需要double类型,是不是和21年蓝桥杯一个思路呢?
整理的规律可以划分成这样:
下面的直线都优先进行去重操作,然后再进行接下来操作
1.如果新增的直线和一个直线平行,那么就只要+1就行了
2.如果新增的直线与平面内所有的直线有交点,且这个交点和之前的交点不一样(所以这样要把交点放进set里面)那么增加的分割数就是交点数+1。
#include <iostream>
#include <set>
using namespace std;
int n;
double A[1005],B[1005];
int main(){
cin>>n;
set<pair<double,double> >a;
while(n--){
double x;
double y;
cin>>x>>y;
a.insert(pair<double,double>(x,y));
}
set<pair<double,double> >:: iterator it=a.begin();
for(int i=0;i<a.size();i++){
A[i]=it->first;
B[i]=it->second;
it++;
}
long long ans = 2;
for(int i = 1; i < a.size(); i++)
{
set<pair< double, double> > pos;
for(int j = 0; j <= i-1; j++)
{
double a1 = A[i], b1 = B[i];
double a2 = A[j], b2 = B[j];
if(a1 == a2) continue;
double x= (b2-b1)/(a1-a2);
double y= a1*(b2-b1)/(a1-a2) + b1;
pos.insert(pair<double,double>(x,y));
}
ans += pos.size() + 1;
}
cout<<ans<<endl;
return 0;
}
字串排序 (25分)

不说了我觉得这题还是比较难的,暂时没有太好的思路,参考别人的答案,代码如下:
#include <bits/stdc++.h>
using namespace std;
const int N = (int)1e4+5;
int num[N];
int main() {
int n, m;
int _max, id, len, sum;
scanf("%d", &n);
sum = 0; len = 0;
while (sum < n) {
id = 1;
for (int i = 2; i <= 26; i++) { //找到s最小的点, 如果存在多个取字典序更小的
if (num[i] < num[id]) id = i;
}
sum = sum + len - num[id];
len ++;
num[id] ++;
}
m = sum - n; //注意更新逆序数差值
for (int i = 1; i <= 26; i++) {
if (num[i]) {
_max = i;
}
}
for (int i = _max; i >= 1; i--) {
for (int j = 0; j < num[i]; j++) {
printf("%c", 'a'+i-1);
}
}
printf("\n");
for (int i = 1; i <= m; i++) {
/*
//尽量消去最大的数字,并且逆序数变化得最少,如果变化量相同则选择字典序较小的方案
id = 0; sum = INT_MAX;
for (int j = 1; j <= 26; j++) {
if (m - i + num[_max] - num[j] >= 0) {
if (sum > num[j] - num[_max] + 1) {
sum = num[j] - num[_max] + 1;
id = j;
}
}
}
if (id) {
num[id] ++;
num[_max] --;
if (!num[_max]) _max--;
i += sum - 1;
printf("~%d\n", id);
continue;
}
*/
for (int j = _max; j >= 1; j--) {
id = 0;
while(num[++id]!= num[j]);
if (id != j) {
num[id] ++;
num[j] --;
break;
}
}
if (!num[_max]) {
_max--;
}
}
for (int i = _max; i >= 1; i--) {
for (int j = 0; j < num[i]; j++) {
printf("%c", 'a'+i-1);
}
}
printf("\n");
return 0;
}