题目来源:牛客,阿里巴巴编程题(2星),第3题
题目描述

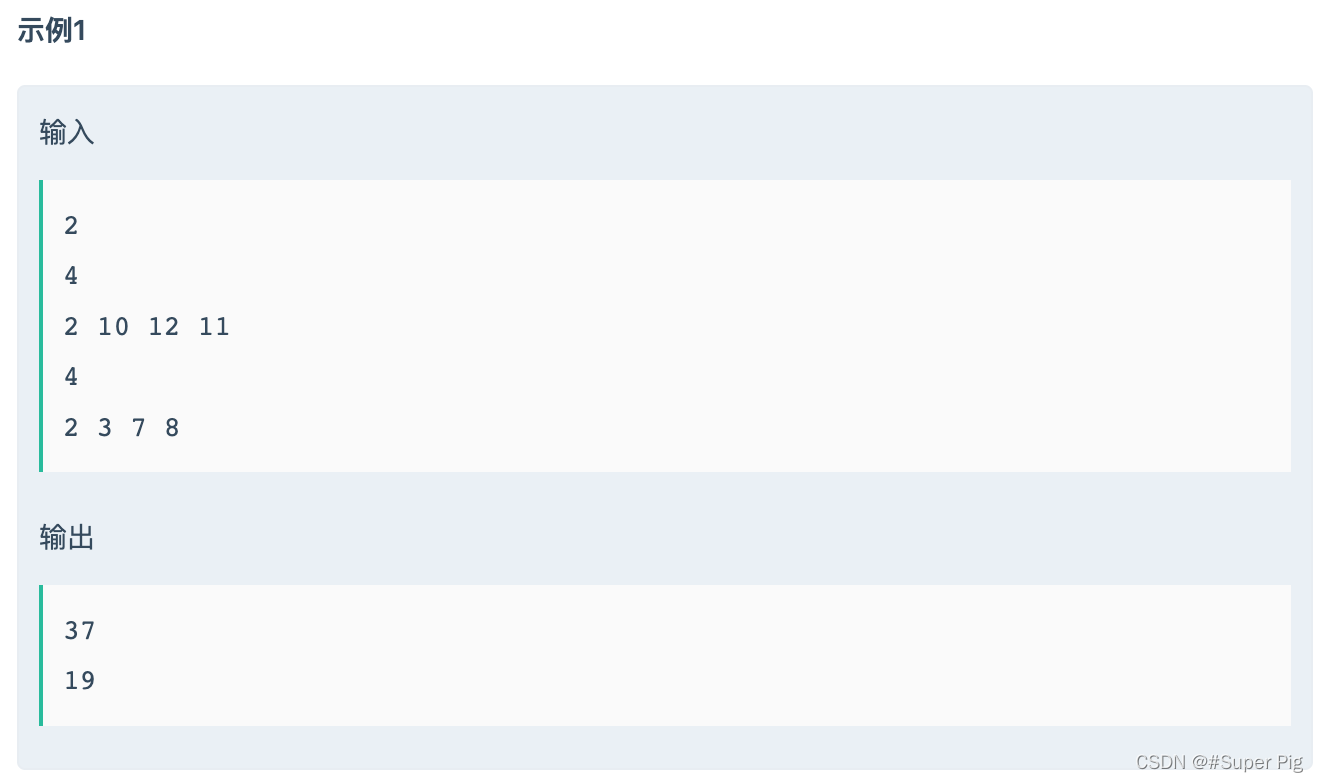
从样例就可以看出,在选择由谁往回划的时候有两种选择方法。
对样例1([2,10,12,11])来说,每次都由最轻的人往回划,这种方法是最省时的;
对样例2([2,3,7,8])来说,如果每次都由最轻的人往回划,这种方法的耗时为22,而样例2给的答案是19。
这时需要转换思路,先搞清楚19是怎么来的:
令time=0;
第一次“往”:2和3一起,time+=3;
第一次“返”:2独自回来,time+=2;
第二次“往”:7和8一起,time+=8;
第二次“返”:3独自回来,time+=3;
第三次“往”:2和3一起,time+=3;
结束,总耗时time=3+2+8+3+3=19。
假设我们从河流左岸出发是“往”,从河流右岸回来是“返”。
至此,我们需要判断什么时候由左岸最轻者“返”,什么时候需要由右岸最轻者“返”。
题解
法一:超时的方法
我在判断由谁负责“返”时,采用了模拟的方法,会不断产生insert和pop的操作,所以超时了,代码如下:
【每一段错误的代码也有被记住的权利-----来自菜狗的卑微】
称“由左岸最轻者“返””的方法为法1,称“由右岸最轻者“返””的方法为法2。
以一次往返为单位,比较两种方法的耗时time和收益gain(即对面增加的重量),由此判断方法选择。
很显然,这样很慢。
def main():
T = int(input())
for i in range(T):
n = int(input())
left = [int(ni) for ni in input().split()]
left.sort()
if n==1:
print(left[0])
continue
elif n==2:
print(left[1])
continue
ans,right = left[0]+left[1],[left.pop(1)]
while len(left)>2:
minleft = left[0]
maxleft = left[-1]
time1 = maxleft+minleft
gain1 = maxleft
midleft = left[-2]
minright = right[0]
time2 = maxleft+minright
gain2 = maxleft+midleft-minright
if gain1-gain2>time1-time2:
ans+=time1
left.pop()
right.append(maxleft)
else:
ans+=time2
left.pop()
left.pop()
right.append(midleft)
right.append(maxleft)
left.insert(1,minright)
ans += left[-1]
print(ans)
return
if __name__=='__main__':
main()
法二:正解
以“两次来回”为单位,比较两种方法的耗时。
当左岸人数小于等于3时,则无须考虑方法选择。
def main():
T = int(input())
for i in range(T):
left,ans = int(input()),0
nums = [int(ni) for ni in input().split()]
nums.sort()
while left>0:
if left==1:
ans+=nums[0]
left=0
elif left==2:
ans+=nums[1]
left=0
elif left==3:
ans+=sum(nums[:3])
left=0
else:
t1 = nums[0]*2+nums[left-1]+nums[left-2]
t2 = nums[0]+nums[1]*2+nums[left-1]
ans+=min(t1,t2)
left-=2
print(ans)
return
if __name__=='__main__':
main()
总结:
解题思路上,太乱【每日一emo】