目录
算法
什么是算法?
算法 (Algorithm): 就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单 来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
算法复杂度
复杂度用来衡量一个算法执行效率好与坏,复杂度又被分为了两个维度去分析,一个是时间复杂度,另一个是空间复杂度。
时间复杂度用来衡量一个算法在运行时,算法执行次数的一个大概的估算。
空间复杂度用来衡量执行一个算法时,该算法在执行时产生的额外空间大小的一个估算。
纠正一个小误区:时间复杂度并不代表一个算法的执行时间,仅代表了一个算法的执行效率。因为执行时间是无法被精准的衡量的,执行时间可能会受到硬件等因素的影响,有时会快有时会慢,所以是无法通过时间的角度去衡量一个算法的优劣。
大O的渐进表示法
“大O的渐进表示法”就是把算法的执行时间或占用空间的一个增长趋势,将代码所有步骤转换成一个以数据N为参数的数学函数。

根据上图推导出公式 : N*N + 2*N +10
N = 10 : F(10)? = 130
N = 100 : F(100) = 10210
N = 1000 : F(1000) = 1000210
可以发现,当N无限大的时候,后两项的2*N+10其实已经对最终的计算结果影响不大了,所以可以几乎忽略不计。比如一个亿万富翁,在酒店给了服务生两百块钱,这两百块钱站在富翁的角度,两百块钱对富翁资产产生的动摇微乎其微,几乎可以忽略不计。所以这里也一样,可以直接去抓大头,只取对结果影响最大的N*N,忽略掉对结果影响不大的项。所以大O的渐进表示法也只是去大概的估算一个算法的执行次数,这里用大O表示法可以表示为O(N^2)。
所以,大O的渐进表示法讨论的不是算法具体的一个执行次数,只讨论这个算法处于哪一个量级。
推导大O阶的方法:
1、常数次用1来表示:例如一个算法要求用O(1)的时间复杂度,不是只能执行1次,而是只能执行常数次。即使那个常数是一亿,但是一亿相较于无穷也不算特别大。
2、只保留对结果影响最大的那一项。
3、当函数的最高项存在且不是1,则除去与该项相乘的常数,得到的结果就是大O阶。例如2*N+10 ,忽略掉常数和相乘的常数表达式就是 N,用 大O的表示法就表示为O(N)。
4、只考虑算法执行时最坏的情况。例如查找,用一个遍历数组长度为N的数组,查找一个数x,可以分为三种情况:
最好的情况:第一个数字就是要找的数字
平均的情况:要找的数字在中间的位置
最坏的情况:要找的数字在最后位置
那么在考虑最坏的情况,要遍历数组就是要执行N次,所以该算法时间复杂度就是O(N)。所以计算时间复杂度是一个悲观的计算,悲观的计算也是最实际的。
时间复杂度分析
一、冒泡排序时间复杂度

先分析最好的情况,当要排序的数组本来就是有序的,就是最好的情况,当它是最好情况是第一遍遍历数据没有发生交换,说明本来就是有序的,exchange等于0跳出循环,就不用去遍历第二遍了,因为是从第二个元素开始遍历的,所以表达式是F(N-1),除去常数项,它的时间复杂度就是O(N)。
最坏情况就是数组是一个完全逆序的数组则:F(N) = (N-1)*N / 2,除去对结果影响不大的常数项得到N*N,所以时间复杂度为O(N^2)
因为时间复杂度是求最坏的情况,所以冒泡排序整体的时间复杂度就是O(N^2)。
注意:并不是两层循环就是N^2 、三层循环就是N^3、N层循环就是N^N,具体还要看程序的具体实现逻辑。
二、二分查找时间复杂度

这是一个左边右开的二分查找,二分查找有三种情况:
最好情况:mid第一次正好就是要查找的数据。
平均情况:在查找到一半的时候就找到了。
最坏情况:当数组被查找完了也没有找到。
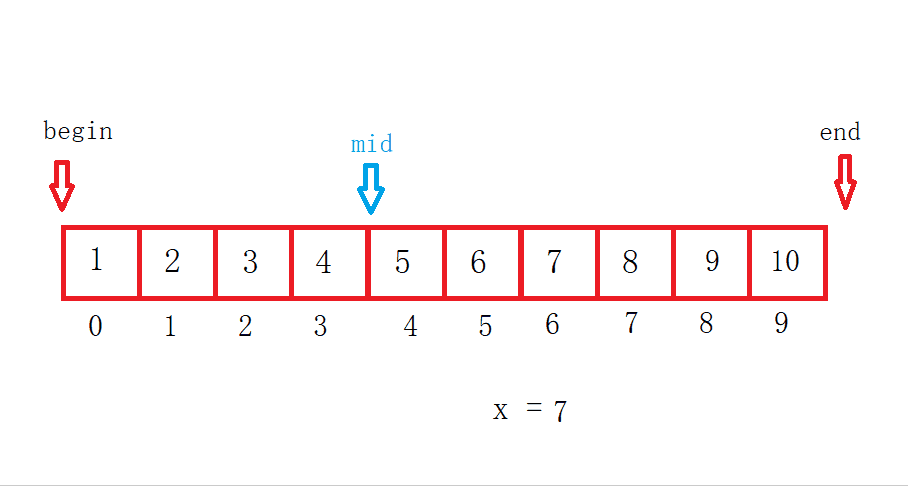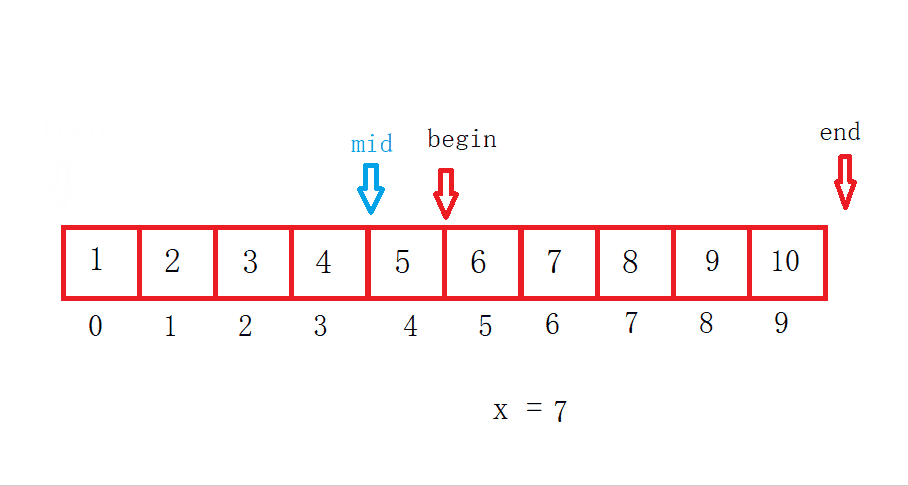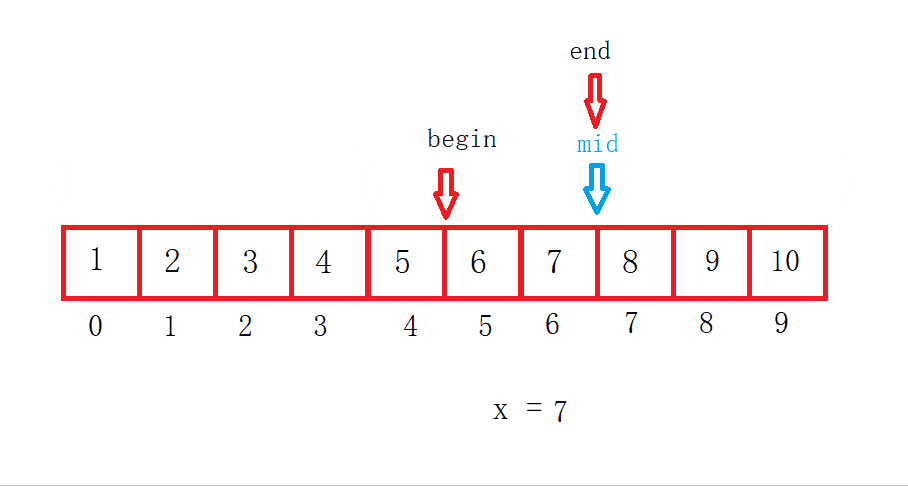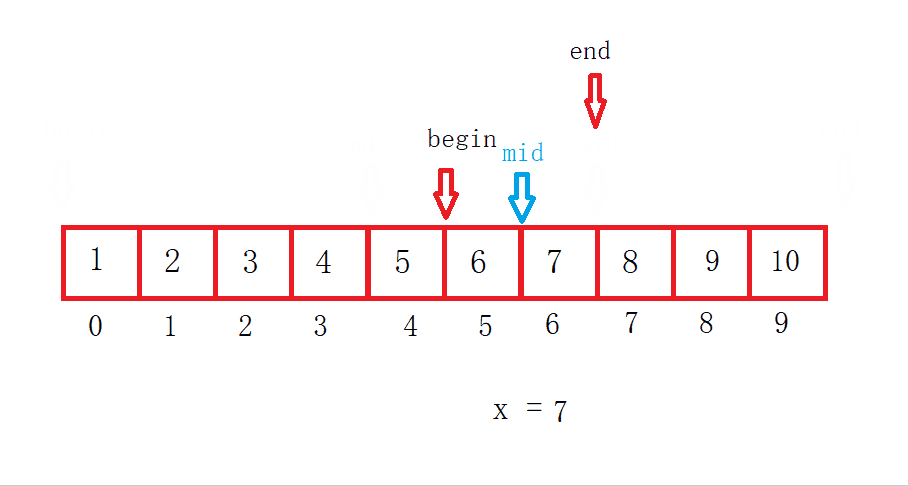
假设数组长度为N,找了X次,那么N = N/2/2/2.../2 = 1时结束。然后表达式逆推一下等于1乘以X个2。

最后求得 log以2为底N 的对数,所以二分查找最坏的时间复杂度就是O(log?N)。
二分查找是一个非常快的算法,假设有1000个数据,O(N)跑1000次,二分查找只需要找10次,有100W个数据,O(N)要跑100W,二分查找只要20次。但使用二分查找的条件比较苛刻,要求这个数组必须是有序的。
三、N的阶乘时间复杂度

阶乘不存在最好和最坏的情况。
要理解递归,最好先画递归的展开图:

?可以发现N = 6时,除去第一次不是递归总共递归了6次,那么N的阶乘的时间复杂度就是O(N)。

如果对这个函数进行了个改造,在里加上一个N层循环,那么时间复杂度就变成O(N^2),所以递归不能只看递归了多少次,也还要计算下递归内部的实际执行次数。
?四、递归的斐波那契数列时间复杂度

用递归实现的斐波那契数列,用递归展开来就是下面这样。
可以把递归分为N层,当递归1层时就有2^0,2层2^1,3层2^2....在第N层时就递归了2^N-1次,也就是2的N-1次方,假设N = 100,就要递归2^100,效率非常的低,斐波那契的递归展开图,就类似于一颗二叉树。它的时间复杂度是O(2^N)

?五、有两个未知数的时间复杂度

因为我们不能确定两个未知数谁大谁小的情况下,我们只能让两个未知数相加起来,那么时间复杂度就是O(N+M)。但是如果题目有说M远大于N或者是N远大于M时,就可以写成O(M) 或者 O(N)。
空间复杂度分析
一、冒泡排序空间复杂度

冒泡排序,这个算法并没有开辟额外的空间,也就是空间是常数次,它的空间复杂度就是O(1)。有些同学对exchange可能会有些存疑,每次循环都会创建一个exchange,为什么不是O(N)呢?
exchange每次在第二层循环执行完之后生命周期结束被销毁,当回到第一层循环时,再创建的exchange其实与上一次的exchange使用的其实是同一块地址空间。
二、额外空间

第一个例子,假设为算法额外开辟一个arr1[100] 数组,因为100是一个常数,所以空间复杂度就是O(1)
第二个例子,开辟了N个空间大小的数组,因为N是未知数没有固定的值,那么它的空间复杂度就是O(N)。
第三个例子,这是一个C99的变长数组,其实和第二个malloc的空间是一样的,N是个未知数,给arr3开辟了N个空间的大小,那么空间复杂度就是O(N)。
三、N的阶乘空间复杂度

N的阶乘,从之前的递归展开图就可以看出,如果算上第一次,总共调用了N+1次函数栈帧,但是忽略常数项就是O(N),那么它的空间复杂度就是O(N)。
四、斐波那契空间复杂度

斐波那契的时间复杂度是O(2^N),那它的空间复杂度是多少呢?如果是光看递归展开图还真不能一眼就看出。这里就用动图来演示:

当N-1的栈帧被销毁后,函数会去调用N-2的栈帧,但是我要说的是,N-2使用的函数栈帧其实就是N-1销毁后还给操作系统的那块空间,证明一下:

可以证明一件事,时间一去不复返,空间可以重复利用,那么斐波那契在递归中调用空间调用了N层的栈帧,那么就使用了N个空间,它的空间复杂度其实就是O(N)。
空间复杂度通常都是O(N)或者O(1),很少碰到像O(N^2)或者O(2^N),(O(2^N)可以说几乎碰不到,因为实在是太大了,栈根本顶不住)。
常见复杂度的对比


?可以看出O(logN)和O(1)几乎就是一条线,非常的快,O(N)线性的增长,再次是O(N*longN),到O(N^2)其实就已经非常慢了,20次就已经执行了400次。最慢的是N的阶乘O(N!)。