大家好,我是耀星🌟,欢迎来到动态规划频道📻。本节主要讲解01背包问题和完全背包问题。背包问题是动态规划中的基础问题,但是并不意味着背包问题很简单。想要彻底的掌握背包问题还是需要花费不少的时间,背包问题又分为,01背包问题、完全背包问题、多重背包问题、混合三种背包问题、二维费用背包问题、分组背包问题、有依赖的背包问题...,想要学习好背包问题,首先要熟练掌握01背包问题,01背包是学习其他背包问题的基础📚,所以非常的重要。
目录
? ?🙆?♂?01背包问题
? ?🙆完全背包问题
? ?🚀Exercises
🙆?♂?01背包问题
👉Example 1(背包问题一)
在
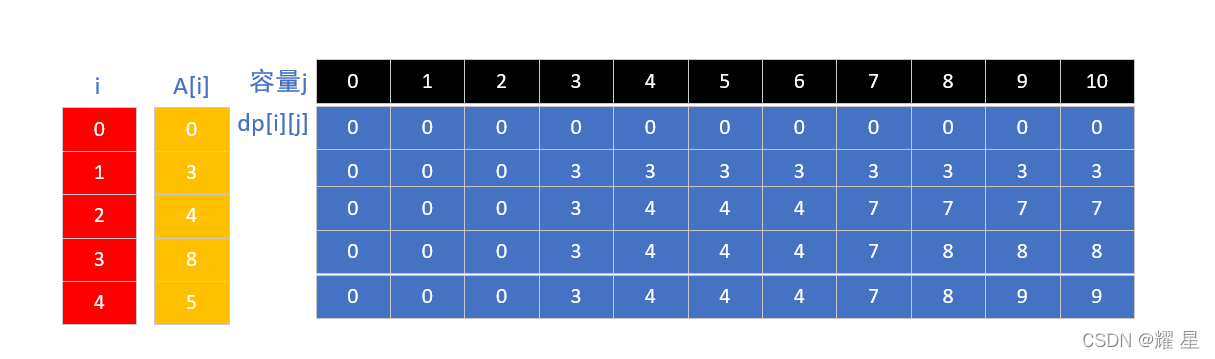
n个物品中挑选若干物品装入背包,最多能装多满?假设背包的大小为m,每个物品的大小为输入:
数组 = [3,4,8,5] backpack size = 10输出:
9解释:装4和5
LintCode链接:背包问题一?????
问题分析:在背包问题中,物品是一个一个选择放入背包,例如背包容量为5,有两个物品第一个重为3,第二个物品重为4,从第一个开始放,可以放入背包则放入,接着放第二个,可以放入背包但是之前已经放入了第一个,这时我们就要判断放入第二个背包是否能装的更满,显然是放入第二个能装的更满 ,就把第一个拿掉,然后放入第二个即可。
?🚑1.确定状态
?当背包容量为m时,有i个物品,设第i个物品的大小为A[i]。如果A[i]>m,那么我们这第i个物品肯定不能装进背包内,因为超过了背包的容量。所以就是要求有i-1个物品时背包能装多满;A[i]<=m,说明该物品可以放进背包,但是把这个物品放进背包并不意味着就能做到背包内装的最满,所以这时我们需要选择性的放。
--如果选择放入背包,背包容量可能还有剩余,比如背包容量为10,物品大小为8,那么容量还剩余2,我们希望剩余的容量也能利用起来,所以我也想知道当容量剩余2时,只有i-1个物品,最多能装多满。容量为2的背包能装的大小+A[i],是我选择将第i个物品后放入背包,背包能装多满。
--如果选择不放入背包,那么背包放的物品大小就是只有i-1个物品时,背包容量为m时装的多满。例如,比如我只有两个物品,第一个物品的大小为5,我背包容量是7,第2个物品的大小为3,不放入第2个物品,比放入第2个物品能装的更满。(放入了第二个物品,第一个物品就放不下)💢到底放不放,取决于放入和不放入哪个能装的更满。
👓子问题:物品个数为i-1个时,背包容量为j-A[i]能够放多满和背包容量为j能够放多满。
💌原问题:物品个数为i个时,背包容量为j时能够放多满。
?状态:dp[i][j]物品个数有i个时,背包容量为j时,背包能装多满.
?🚄2.转移方程
打表法确定状态转移方程式:
🚍3.初始条件及边界情况
初始条件:
dp[0][0] = dp[0][1] = dp[0][2]=...=dp[0][m] = 0?
🚖4.计算顺序
dp[0][0] dp[0][1] dp[0][2]...
dp[1][0] dp[1][1] dp[1][2]..
...?
空间优化?
我们可以从状态转移方程式中可以看出当我们计算dp[i][j]时只需要用到其上一行数据,可以使用滚动数组优化,还有更好的优化方案吗?
👇解法1:(普通版)
public class Solution {
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @return: The maximum size
*/
public int backPack(int m, int[] A) {
// write your code here
int n = A.length;
if(m == 0 || A == null || n==0)
{
return 0;
}
int[][] dp = new int [n+1][m+1];
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
if(j>=A[i-1]){
dp[i][j] = Math.max(dp[i-1][j], dp[i-1][j-A[i-1]]+A[i-1]);
}else{
dp[i][j] = dp[i-1][j];
}
}
}
return dp[n][m];
}
}👇解法2(优化版)?
public class Solution {
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @return: The maximum size
*/
public int backPack(int m, int[] A) {
int n = A.length;
if(m == 0 || A == null || n==0)
{
return 0;
}
int[] dp = new int [m+1];
for(int i=1; i<=n; i++){
for(int j=m; j>=A[i-1]; j--){
dp[j] = Math.max(dp[j], dp[j-A[i-1]]+A[i-1]);
}
}
return dp[m];
}
}?👉Example 2(背包问题二)
有?
n?个物品和一个大小为?m?的背包. 给定数组?A?表示每个物品的大小和数组?V?表示每个物品的价值.问最多能装入背包的总价值是多大?
A[i], V[i], n, m?均为整数- 你不能将物品进行切分
- 你所挑选的要装入背包的物品的总大小不能超过?
m- 每个物品只能取一次
- m <= 1000
len(A),len(V)<=100
输入:
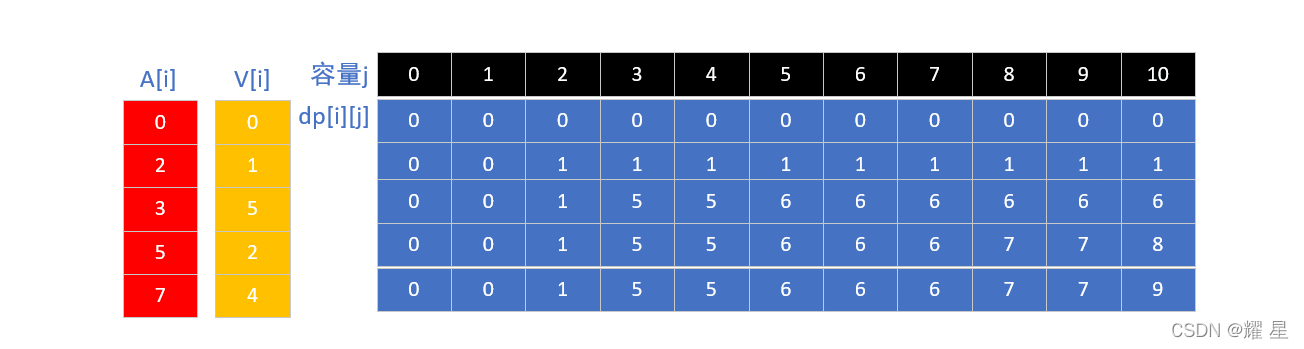
m = 10 A = [2, 3, 5, 7] V = [1, 5, 2, 4]输出:
9解释:
装入 A[1] 和 A[3] 可以得到最大价值, V[1] + V[3] = 9
LintCode链接:背包问题二
🚐1.确定状态
同理,和背包问题一类似,背包1是装的最满,背包问题二是能够装的价值最大,且不超过背包的容量。
🚑2.转移方程
打表法确定状态转移方程式
🚀3.初始条件及边界情况
初始条件:
dp[0][0] = dp[0][1] = dp[0][2]=...=dp[0][m] = 0?
🚋4.计算顺序
dp[0][0] dp[0][1] dp[0][2]...
dp[1][0] dp[1][1] dp[1][2]..
...?
public class Solution {
/**
* @param m: An integer m denotes the size of a backpack
* @param A: Given n items with size A[i]
* @param V: Given n items with value V[i]
* @return: The maximum value
*/
public int backPackII(int m, int[] A, int[] V) {
int n = A.length;
int[] dp = new int[m+1];
for(int i=1; i<=n; i++){
for(int j=m; j>=A[i-1]; j--){
dp[j] = Math.max(dp[j], dp[j-A[i-1]]+V[i-1]);//转移方程,经过空间优化
}
}
return dp[m];
}
}🙆完全背包问题
👉Example 1(背包问题三)
给定?
n?种物品, 每种物品都有无限个. 第?i?个物品的体积为?A[i], 价值为?V[i].再给定一个容量为?
m?的背包. 问可以装入背包的最大价值是多少?样例 :
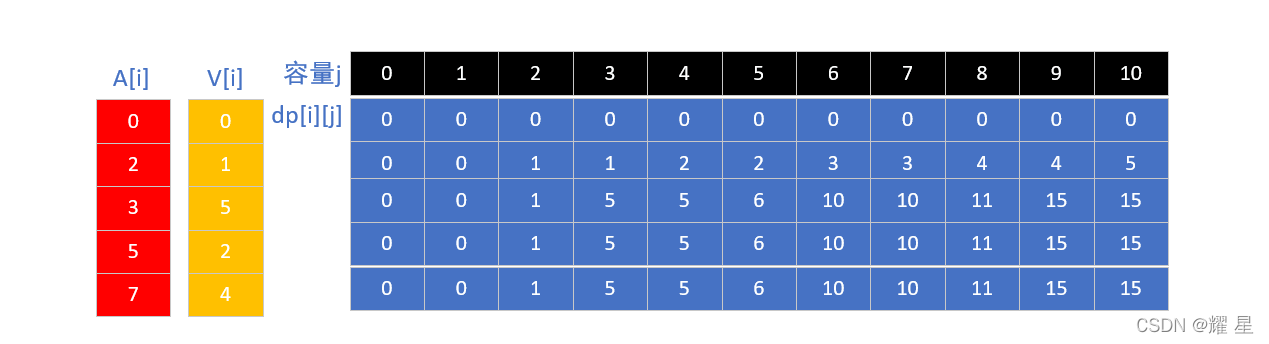
输入: A = [1, 2, 3], V = [1, 2, 3], m = 5 输出: 5 解释: 策略不唯一. 比如, 装入五个物品 0 (A[0] = 1, V[0] = 1).LintCode链接:背包问题三
🚙1.确定状态
每种物品都有无限个,只要在背包容量允许下,尽可能装的价值大。
假设只有一个物品,物品大小为2价值为3,背包容量为5,那么你一定会选择装两个该物品,价值最大。
假设有两个物品,物品1大小为2价值为3,物品2大小为3价值为2。背包容量为5,可以选择装两个物品1价值为6,也可以选择装一个物品1一个物品2,价值为5,显然不可取。
假设我们现在要放入第j个物品,如果第j个物品能够放入背包,那么我们就要判断放入背包能不能使背包达到最大价值,选择放入背包,我们如果知道放入背包后剩余的容量j-A[i]能够放的最大价值,那么就能知道该物品放入背包能够达到的价值。如果选择不放入背包,只要知道有i-1个物品时,背包容量为j时,背包能够放的最大价值。选择其中一个较大值既是最优策略。
🎉原问题:物品个数为i个时,背包容量为j能够装的最大价值
😜子问题:物品个数为i个时,背包容量为j-A[i]能够装的最大价值,物品个数为i-1个时,背包容量为j能够装的最大价值。
🐢状态:dp[i][j]有i个物品时,容量为j的背包能够装的最大价值。
🚖2.转移方程
打表法确定状态转移方程
🚀3.初始条件及边界情况
初始条件:
dp[0][0] = dp[0][1] = dp[0][2]=...=dp[0][m] = 0
🚋4.计算顺序
dp[0][0] dp[0][1] dp[0][2]...
dp[1][0] dp[1][1] dp[1][2]..
...??
public class Solution {
/**
* @param A: an integer array
* @param V: an integer array
* @param m: An integer
* @return: an array
*/
public int backPackIII(int[] A, int[] V, int m) {
int n = A.length;
if(n == 0 || A == null || m == 0){
return 0;
}
int[] dp = new int[m+1];
for(int i=1; i<=n; i++){
for(int j=1; j<=m; j++){
if(j>=A[i-1]){
dp[j] = Math.max(dp[j],dp[j-A[i-1]]+V[i-1]);//经过空间优化
}
}
}
return dp[m];
}
}🚀Exercises
👉Example 1(背包问题V)
给出 n 个物品, 以及一个数组,?
nums[i]?代表第i个物品的大小, 保证大小均为正数, 正整数?target?表示背包的大小, 找到能填满背包的方案数。每一个物品只能使用一次样例:
给出候选物品集合?
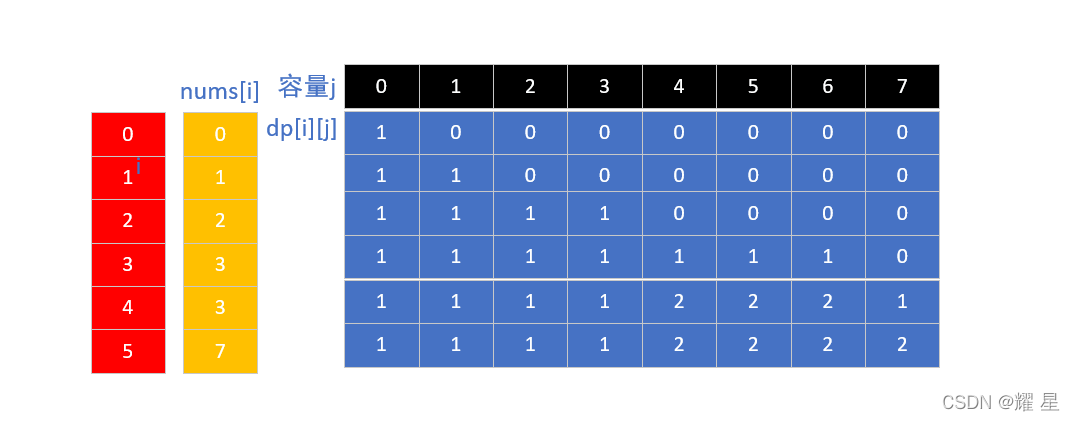
[1,2,3,3,7]?以及 target?7结果的集合为: [7] [1,3,3]返回?
2
LintCode链接:背包问题 V
🚙1.确定状态?
🎑最后一步:
设有n个物品时,背包容量为target能填满背包的方案数为N,如果我们知道有n-1个物品时(第n个物品不放入背包),能填满背包的方案数N1。且知道(第i个物品放入背包)能填满背包的方案数N2。则填满背包容量为target的方案数N=N1+N2
🎉子问题:n-1个物品能填满背包容量为target的方案数,和n-1个物品能填满背包容量为(target-nums[n])的方案数
💥原问题:n个物品能够填满背包容量为target的方案数。
👌状态:dp[i][j]当有i个物品时能够填满背包容量为j的方案数。
🚓2.转移方程?
打表法确定状态转移方程
🚎3. 初始条件及边界情况
初始条件:
当物品有i个且时背包容量为0时,有1种填满方案。
dp[0][0] = 1dp[1][0] = 1;....dp[n][0] = 1
🎡4.计算顺序?
dp[0][0] dp[0][1]..dp[0][target]
dp[1][0] dp[1][1]..dp[1][target]
....?
👇解法1:普通版?
public class Solution {
/**
* @param nums: an integer array and all positive numbers
* @param target: An integer
* @return: An integer
*/
public int backPackV(int[] nums, int target) {
int n = nums.length;
if(n == 0 || nums == null){
return 0;
}
int[][] dp = new int[n+1][target+1];
//初始化
dp[0][0] = 1;
for(int i=1; i<=target; i++){
dp[0][i] = 0;
}
for(int i=1; i<=n; i++){
dp[i][0] = 1;
for(int j=1; j<=target; j++){
//情况1
dp[i][j] =dp[i-1][j];
//情况2
if(j>=nums[i-1]){
dp[i][j]+=dp[i-1][j-nums[i-1]];
}
}
}
return dp[n][target];
}
}👇解法2:优化版?
public class Solution {
/**
* @param nums: an integer array and all positive numbers
* @param target: An integer
* @return: An integer
*/
public int backPackV(int[] nums, int target) {
int n = nums.length;
if(n == 0 || nums == null){
return 0;
}
int[] dp = new int[target+1];
dp[0] = 1;//初始化
for(int i=1; i<=n; i++){
for(int j=target; j>=nums[i-1]; j--){
dp[j]+=dp[j-nums[i-1]];
}
}
return dp[target];
}
}👉Example 2(组合总和IV)
?给出一个都是正整数的数组?
nums,其中没有重复的数。从中找出所有的和为?target?的组合个数。样例:
输入: nums = [1, 2, 4] 和 target = 4 输出: 6 解释: 可能的所有组合有: [1, 1, 1, 1] [1, 1, 2] [1, 2, 1] [2, 1, 1] [2, 2] [4]LintCode链接:组合总和 IV
如果组合没有重复的,那么使用完全背包解决。这题可以看成跳台阶问题。
🚙1.确定状态
🥠最后一步
求青蛙一次可以跳
阶能够到达target层的方案数。最后一步一定是从target-
层跳到第target层,所以只要知道跳到第target-
层有多少种方案即可。
一次跳只能跳1阶:跳到第四层的方案。
1->1->1->1
dp[4] = dp[4-1]
一次能跳1阶或2阶:跳到第四层的方案。
1->1->2
1->2-1
2->1->1
2->2
dp[4] = dp[4-1] +dp[4-2]
一次能跳1阶或2阶或4阶
dp[4] = dp[4-1] + dp[4-2] + dp[4-4]
?子问题:跳到(target-
)层,有多少种方案。
🎐原问题:跳到target层有多少种方案。
🤡状态:dp[i]表示一次可以跳
阶跳到第i层的方案数。
🚐2.转移方程?
🛴3.初始条件及边界情况?
初始条件
dp[0] = 1;
🚅4.计算顺序?
dp[0] dp[1] ...dp[target]
public class Solution {
/**
* @param nums: an integer array and all positive numbers, no duplicates
* @param target: An integer
* @return: An integer
*/
public int backPackVI(int[] nums, int target) {
if (nums == null || nums.length == 0){
return 0;
}
int[] dp = new int[target+1];
dp[0] = 1;
for(int i=1; i<=target; i++){
for(int j=1; j<=nums.length; j++){
if(nums[j-1]<=i){
dp[i] += dp[i-nums[j-1]];
}
}
}
return dp[target];
}
}水平有限🕹,希望能够对大家有帮助,感谢大家的支持?。