题目一:货物摆放

现在设这个立方体的长宽高为a,b,c,即必须满足abc=n,有这个式子可得,啊a,b,c都是的因子,因此这道题可以转化为找到n的因子,在n的因子中如果三个因子相乘为n,则符合要求,现在考虑如何找到这个数的因子,刚开始考虑的时候,是将小于n的数遍历一遍,如果相除的余数为0,则是该数的因子,如果数小可以采用,但是如果数像这道题中这么大,计算机跑起来会花费很多时间,因此我们可以考虑求到根号n,也就是说如果i是n的因子,则n/i也是n的因子
所以大致思路就是,定义一个变量i,在i*i<=n时开始遍历,寻找对应的因子,定义一个数组来存放找到的因子,如果n%i=0,则i是n的因子,存放到数组中,同是如果n/i!=i,则n/i也是n的因子,也将其存放到数组当中,因为根据题目来讲,将三个因子来回颠倒顺序是不同的方案,因此将数组中的元素遍历,只要三个元素相乘等于n即可,用计数器计算个数就可以啦
#include <iostream>
using namespace std;
int main()
{
long long arr[1000];//定义数组存放因子
// 请在此输入您的代码
long long n=2021041820210418;
int length=0;
long long i=1;
for(i=1;i*i<=n;i++)
{
if(n%i==0)
{
arr[length]=i;
length++;
if(n/i!=i)//要考虑两个元素相同的情况
{
arr[length]=n/i;
length++;
}
}
}
long long x,y,z;
long long count=0;
for(x=0;x<length;x++)
{
for(y=0;y<length;y++)
{
if(arr[x]*arr[y]>n)
continue;
for(z=0;z<length;z++)
{
if(arr[x]*arr[y]*arr[z]==n)
{
count++;
}
}
}
}
cout<<count<<endl;
return 0;
}
总结:
有相乘问题的话要考虑找到该数的因子,但是不能都是暴力地遍历,要考虑如果i是因子,则n/i也是,所以遍历到根号n即可呀
在考虑存放n/i这个因子的时候,要考虑n/i是不是等于i的情况,否则可能因子多出一个
题目二:路径问题

这道题就是一个求最短路径的问题,可以采用多种算法,我这里用的是比较暴力的Floyd算法,就是定义一个二维数组来存储路径长度,引入一个中间值k,进行比较来确定这个最短路径,这里我就不再详细介绍算法的思路了,主要说一下总结出来的问题
#include <iostream>
using namespace std;
const int MAX=3000;
const long long INF = 1e18;
long long arr[MAX][MAX];
void Floyd(int n)
{
for(int k=1;k<=n;k++)
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
if(arr[i][j]>arr[i][k]+arr[k][j])
{
arr[i][j]=arr[i][k]+arr[k][j];
}
}
}
}
}
int number(int x,int y)//找最大公约数
{
int i=x;
if(x>y)
i=y;
while(i)
{
if((x%i==0)&&(y%i==0))
{
return i;
}
i--;
}
}
int abs(int x,int y)//计算绝对值
{
if(x>=y)
return x-y;
else
return y-x;
}
int main()
{
int n=2021;
for(int i=1;i<=n;i++)//将数组初始化
{
for(int j=1;j<=n;j++)
{
if(i==j)
{
arr[i][j]=0;
}
else if(abs(i,j)<=21)
{
arr[i][j]=arr[j][i]=i*j/number(i,j);
}
else
{
arr[i][j]=INF;
}
}
}
Floyd(n);
cout<<arr[1][2021]<<endl;
return 0;
}
求最小公倍数即两数相乘再除以最大公约数
结果附上:
题目三:蛇形填数
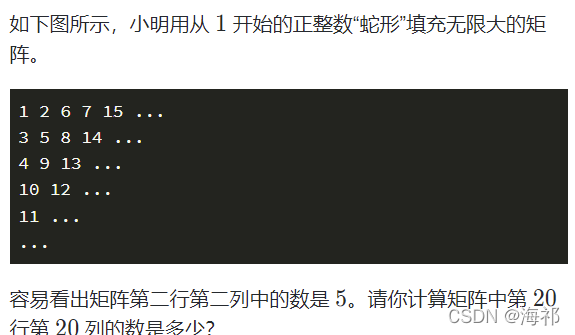
对于这种题目,如果数值比较小,就可以考虑直接用手动列举的方法,但是如果数据较大,就不可采用
对于这种问题,要考虑找规律,在填写的时候,会有斜着向上和斜着向下两种填法,而数据是依次递增的,所以我们可以类比计数器来记录数据,然后只考虑行和列的变化就可以了,当然,也要必须考虑边界问题,即第一行和第一列的数据
设r来表示行数,s来表示列数,我们就可以考虑行数的变化规律
(1)r=1时:
c为奇数:下一步将走到(r,c+1)
c为偶数:下一步将走到(r+1,c-1)
(2)c=1时
r为奇数:下一步将走到(r-1,c+1)
r为偶数:下一步将走到(r+1,c)
(3)接下来就要考虑其他数据了,因为每次写的时候是斜着的,所以这斜着的一行行数+列数的奇偶性是相同的,因此可以根据行数和列数相加的奇偶性来判断下一步的走向
r+c为奇数时:下一步将走到(r+1,c-1)
r+c为偶数时:下一步将走到(r-1,c+1)
由此经过循环就可以求出其对应数字啦
#include <iostream>
using namespace std;
int main()
{
int r=1;int c=1;
int n=1;
while(r!=20||c!=20)
{
if(r==1)
{
if(c%2==0)
{
r++;
c--;
}
else
{
c++;
}
}
else if(c==1)
{
if(r%2==0)
{
r++;
}
else
{
r--;
c++;
}
}
else if((r+c)%2==0)
{
r--;
c++;
}
else
{
r++;
c--;
}
n++;
}
cout<<n<<endl;
return 0;
}
锵锵锵!放上结果来
总结:对于复杂的数据问题,要考虑找其中的规律,再二位数组中或者矩阵里,更要考虑找行和列的规律,当然,要着重考虑特殊情况,即行和列为1的情况
