参考:算法导论
插入
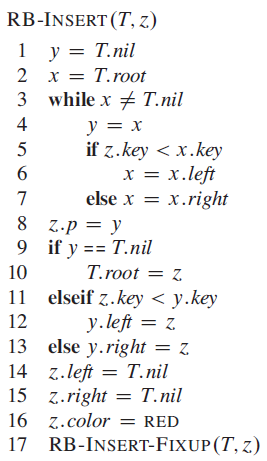
利用二叉搜索树的性质,二分到合适的位置,插入一个红色的叶节点(设为 z)。
插入修正(双红修正)
如果 z.p 也是红色,那么将违反第 4 条性质(红节点的子节点是黑节点),需要进行修正,过程如下:

Case 1:叔节点(y)为红色
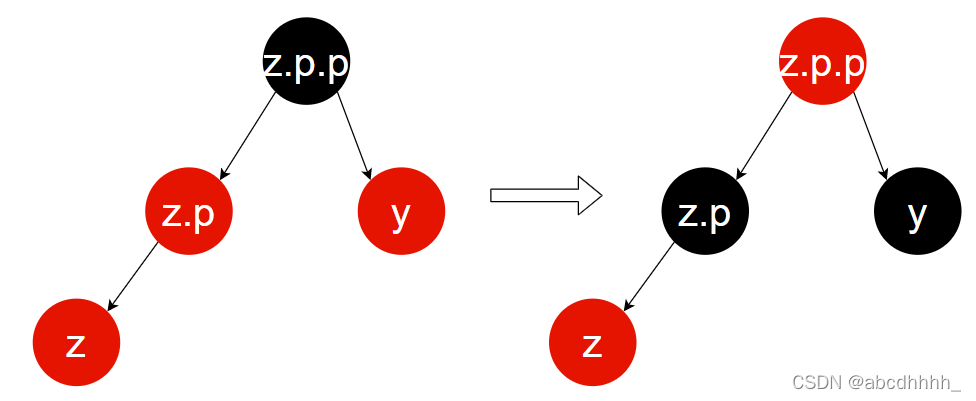
更改 z.p ,z.p.p ,y 的颜色
将问题上传至 z.p.p
Case 2:叔节点(y)为黑色,z ,z.p ,z.p.p 不共线
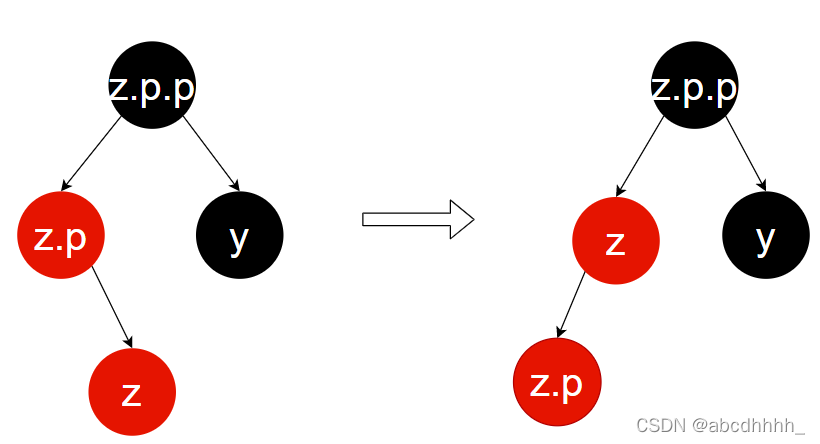
旋转 z
归约到 Case 3
Case 3:叔节点(y)为黑色,z ,z.p ,z.p.p 共线
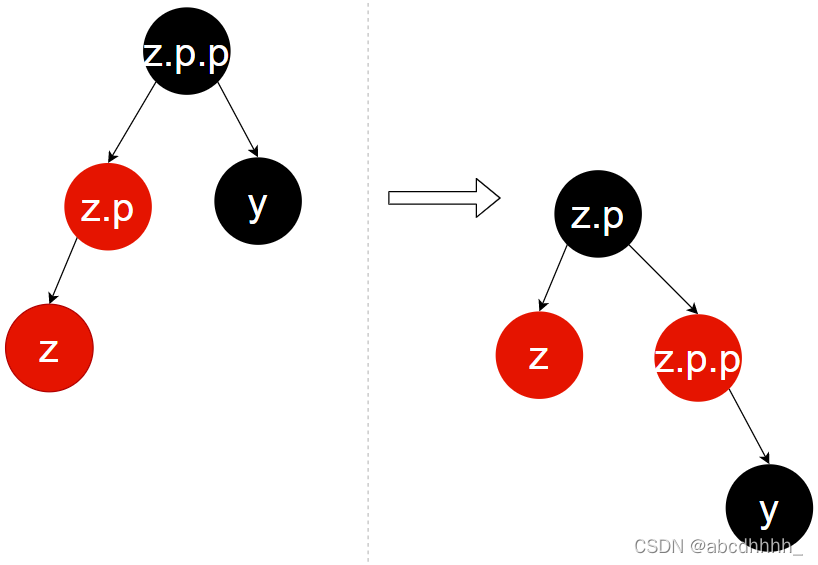
更改 z.p ,z.p.p 的颜色,旋转 z.p
删除


第 13 行是多余的
若 z 的左右子节点均非空,则交换它和它的后继(但不交换颜色),然后归约为删除它的后继。
若 z 有一个空子节点,则用另一个子节点对应子树替换它。
如果 z 是黑色,那么将违反第 5 条性质(叶节点黑高相等),需要进行修正,过程如下(设 x 对应子树黑高少了 1):

若 x 为根,问题已消除。
若 x 为红色,将 x 修改为黑色即可。
否则:
Case 1:兄弟节点(w)为红色
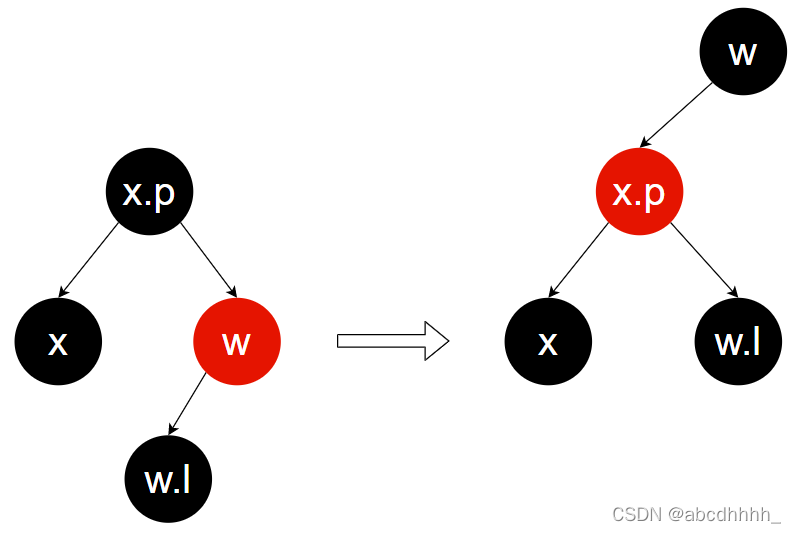
更改 w ,x.p 的颜色,旋转 w
归约为 Case 2-4
Case 2:兄弟节点(w)为黑色,兄弟节点子节点(w.l,w.r)均为黑色
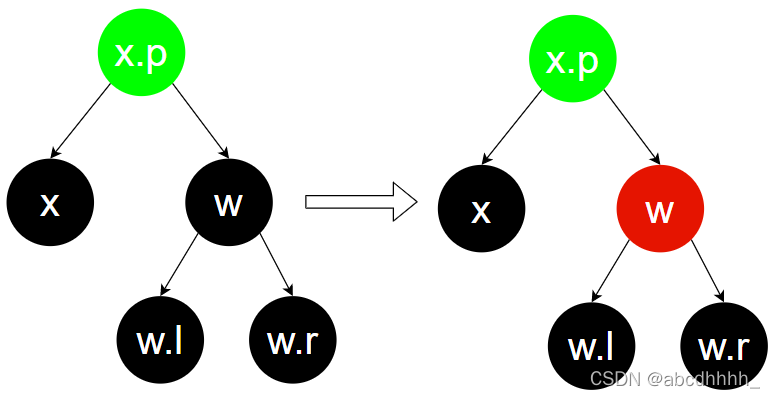
更改 w 的颜色
将问题上传至 x.p
Case 3:兄弟节点(w)为黑色,兄弟节点子节点左(w.l)红右(w.r)黑
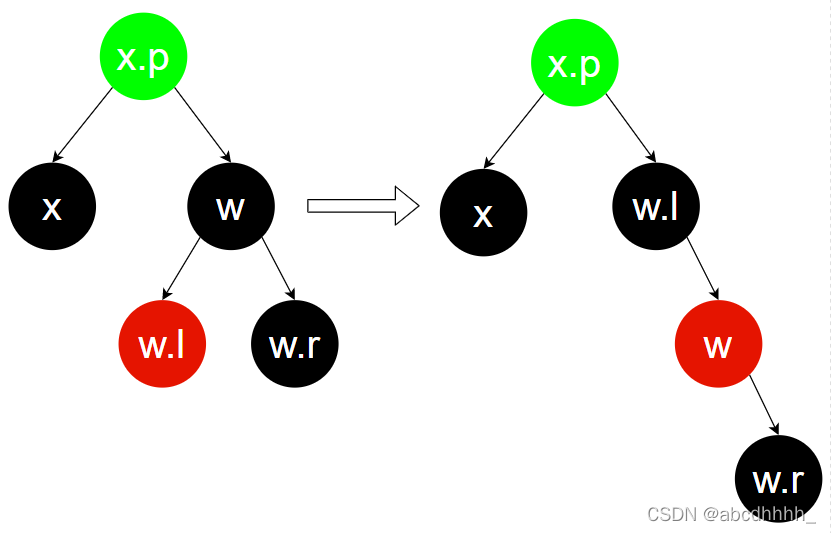
更改 w ,w.l 的颜色,旋转 w.l
归约为 Case 4
Case 4:兄弟节点(w)为黑色,兄弟节点右子节点(w.r)为红色
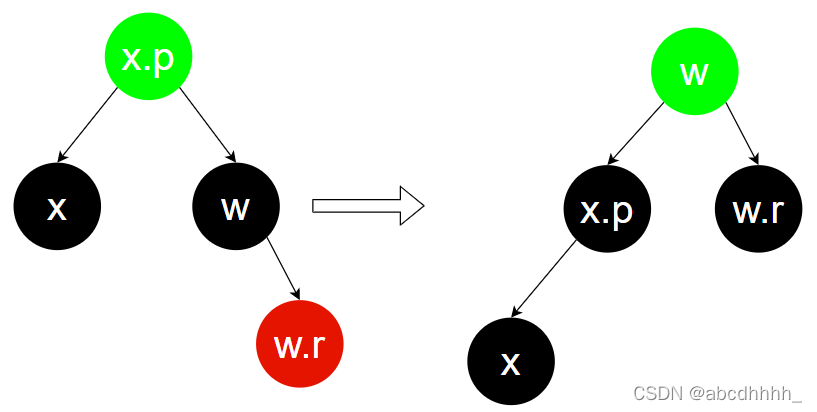
更改 w.r 的颜色
交换 x.p ,w 的颜色,旋转 w