🤞冲刺蓝桥 距离【第十三届蓝桥杯4月9日省赛】仅剩【04天】 🤞
📢今日题目:蓝桥杯真题
🍺刷题一览

往期文章推荐-------0基础算法系列
2019省赛b组c++
明码

10个汉字是 : 九的九次方等于多少?
答案: 387420489
#include<iostream>
using namespace std;
int main(){
int m,n;
int w[16];
while( cin>>m>>n ){
for(int i=7;i>=0;i--){
w[i]=m&1;
m>>=1;
}
for(int i=15;i>=8;i--){
w[i]=n&1;
n>>=1;
}
for(int i=0;i<=15;i++){
if( w[i] == 1 )
cout<<w[i];
else cout <<" ";
}
cout<<endl;
}
}
乘积为0

要想乘积为零的话,只有2和5才能出0.那么我们记录有多少个2和多少个5取最小值就行了。
#include<iostream>
#define ll long long
using namespace std;
int main()
{
ll sum2=0;
ll sum5=0;
int x;
for(int i=1;i<=100;i++)
{
cin>>x;
while(x)
{
if(x%2==0) x/=2,sum2++;
else break;
}
while(x)
{
if(x%5==0) x/=5,sum5++;
else break;
}
}
cout<<min(sum2,sum5)<<endl;
return 0;
}
测试次数

假设 第 1 次随便随便选一层扔 ,选 第 层 碎了,碎了我也有2部手机不是,
那么 我此时想用两部手机测出 1~( -1)范围的耐摔指数就和上面情况一样的
最坏测试次数满足关系 k*(k+1)/2>=-1= -1 (同时保证 k+1<=K,=>k<=K-1注 :这是大 K )
若没碎就可以进行下一步
假设 第 2 次随便随便选一层扔 ,选第 层 碎了,碎了我也有2部手机不是,
那么 我此时想用两部手机测出 ( +1)~( -1)范围的耐摔指数就和上面情况一样的
最坏测试次数满足关系 k*(k+1)/2>=( ???????-1)- =???????- -1 (同时保证 k+1+1 <=K,=>k<=K-2注 :这是大 K)
若没碎就可以进行下一步
假设 第 3 次随便随便选一层扔 ,选第 层 碎了,碎了我也有2部手机不是,
那么 我此时想用两部手机测出( +1)~( -1)范围的耐摔指数就和上面情况一样的
最坏测试次数满足关系 k*(k+1)/2>=( -1)-??????? =???????- ???????-1 (同时保证 k+1+1+1 <=K,===>k<=K-3注 :这是大 K)
。
。
。
假设 第 k次随便随便选一层扔 ,选第 层 碎了,那么只好 碎了我也有2部手机不是,
那么 我此时想用两部手机测出(???????+1)~( -1)范围的耐摔指数就和上面情况一样的
最坏测试次数满足关系 k*(k+1)/2>=( -1)-( ???????+1)=???????- ??????? -1(同时保证 k+1+1…+1 <=K,===>k<=K-K注 :这是大 K)
如法炮制 但是这里的小k 每行是不一样的所以要将他们 用大K 替换掉
k*(k+1)/2>=-1= -1 k<=K-1
k*(k+1)/2>=( ???????-1)- =???????- -1 k<=K-2
k*(k+1)/2>=( -1)- ??????? =???????- ???????-1 k<=K-3
......
k*(k+1)/2>=( -1)- ???????=???????- ??????? -1 k<=K-K
替换后:
(K-1)*K/2>=-1= -1
(K-2)*(K-1)/2>=( ???????-1)- =???????- -1
(K-3)*(K-2)/2>=( -1)- ???????=???????- ???????-1
......
(K-K)*(K-(K-1))/2>=( -1)- ???????=???????- ??????? -1
消消元: 1/2* [(K-1)K+ (K-2)(K-1)+(K-3)(K-2)…(K-K)(K-(K-1))]>=-K
配凑法: 1/2* [k2+(K-1)2+ (K-2)2+(K-3)2…(K-(k-1))^2]-[K+(K-1)+(K-2)+(k-3)…+(K-(K-1))]>=-K
(同时增加减少 [K+(K-1)+(K-2)......(K-(K-1))]- [K+(K-1)+(K-2)......(K-(K-1))+(K-K)] )
两边化简一下:1/2* [K2+(K-1)2+ (K-2)2+(K-3)2…1^2]-[K+(K-1)+(K-2)+(k-3)…+(K-(K-1))+(K-K)]>=-K
===>1/2* [K^2+(K-1)^2+ (K-2)^2+(K-3)^2......1^2]-[K*(K+1)-1-2-3.....-K]>=-K
根据平方求和公式 :
所以 原式等于 1/2*{ K*(K+1)(2K+1)/6 -[K*(K+1)-K*(K+1)/2]>=-K
====>1/2*{ K*(K+1)(2K+1)/6 -[K*(K+1)-K*(K+1)/2]>=-K
====> (K^3+5K)/6 >= ==1000
====> K=19
于是就得到了 公式
#include<stdio.h>
int main(){
int i;
for(i=0;i<100;i++)
if((i*i*i+i*5)/6>=1000)break;
printf("%d\n",i);
return 0;
}
快速排序

a, i+1, r, k-(i-l+1)
注意时间复杂度的要求
递增三元组

#include<iostream>
#include<algorithm>
using namespace std;
//4
//1 3 4 5
//1 2 2 2
//2 3 3 4
int a[100010];
int b[100010];
int c[100010];
int n;
long long ans = 0;
int main(){
//输入数据
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
cin>>b[i];
}
for(int i=1;i<=n;i++){
cin>>c[i];
}
//排序
sort(a+1,a+n+1);
sort(b+1,b+n+1);
sort(c+1,c+n+1);
//定义两个指针(下标)
int j = 1;
int k = 1;
//以b为中间值 在a数组 c数组中查找
for(int i=1;i<=n;i++){
while(j<=n && a[j] < b[i]) j++; //在a数组中查找第一个大于等于b[i]的数
while(k<=n && c[k] <= b[i]) k++; //在c数组中查找第一个大于b[i]的数
ans += (long long)(j-1) * (n-k+1); //计算公式 可以自己举例推导出来
}
cout<<ans<<endl;
return 0;
}
日志统计
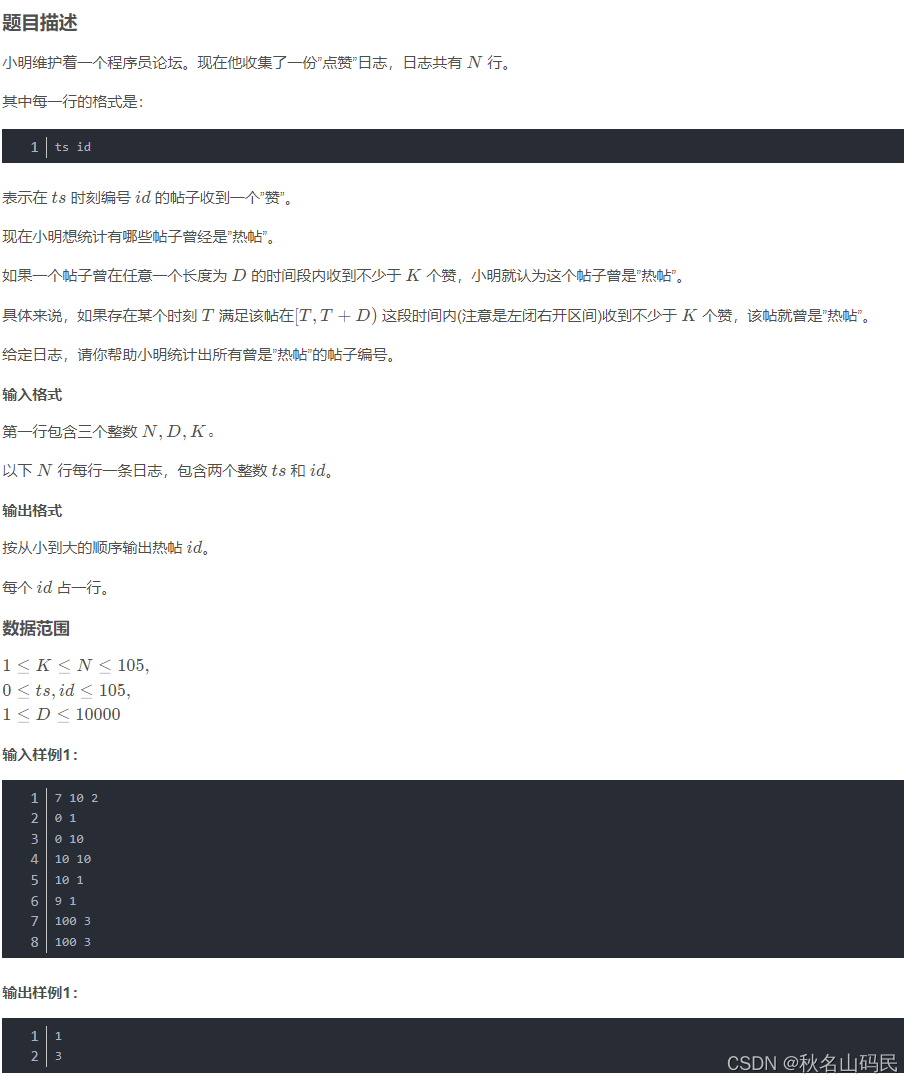
//双指针
#include <iostream>
#include <algorithm>
using namespace std;
#define x first
#define y second
typedef pair<int,int> PII;
const int N = 100010;
PII w[N];
int cnt[N];
bool res[N]; // 存放答案
int n, d, k;
int main()
{
cin >> n >> d >> k;
int a, b;
for(int i = 0;i < n;i ++) {
scanf("%d%d",&a,&b);
w[i] = {a,b};
}
sort(w,w + n);
for(int i = 0,j = 0;i < n;i ++) {
while(j < n && w[j].x - w[i].x < d){
cnt[w[j].y] ++;
if(cnt[w[j].y] >= k) res[w[j].y] = true;
j ++;
}
cnt[w[i].y] --;
}
for(int i = 0;i < N;i ++)
if(res[i]) printf("%d\n",i);
return 0;
}
全球变暖

#include<bits/stdc++.h>
using namespace std;
const int N=1e4+5,NN=1e7+5;
long ans=0,ansd=0;//ansd记录岛屿数量(或编号)
int a[NN];//记录不会被淹没的陆地的数量的数组
char ma[N][N],vis[N][N];
//mas数组记录照片信息,vis数组为访问数组,被访问置1
int nx[4]={0,0,1,-1};
int ny[4]={1,-1,0,0};
//方向数组
void bfs(int x,int y,int k){
int flag=1,i=0;
while(flag){
if(i==4) break;
if(ma[x+nx[i]][y+ny[i]]=='.') flag=0;
i++;
}
if(i==4 and flag==1){
a[k]++;
}
//判断是不是不会被淹没的陆地
vis[x][y]=1;
for(int j=0;j<4;j++){
int nx1=x+nx[j];
int ny1=y+ny[j];
if(vis[x+nx[j]][y+ny[j]]==0
and ma[x+nx[j]][y+ny[j]]=='#') bfs(nx1,ny1,k);
}
}
int main(){
int n;
cin>>n;
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
cin>>ma[i][j];
}
}
for(int i=1;i<=n;i++){
for(int j=1;j<=n;j++){
if(ma[i][j]=='#' and vis[i][j]==0) ansd++,bfs(i,j,ansd);
}
}
for(int i=1;i<=ansd;i++){
if(a[i]==0) ans++;
}
cout<<ans<<endl;
}