[数据结构与算法]01背包（动态规划）

?01背包_牛客题霸_牛客网 (nowcoder.com)

最近不是学习了动态规划吗，来回顾一下之前不是特别理解的01背包问题?

老规矩，动态规划三步走入门动态规划之三步走

• 第一步定义dp数组含义，我们这里根据题意选择定义二维数组dp[i][j]为只有前i个物品在容量为??j?的背包下我们能获得的最大重量（或者说对于dp[ i ][ j ]来说，i指的是前i件物品，j指的是还剩多少的背包空间）
• 第二步寻找数组元素之间的关系式

对于我们面对一件物品来说，我们有两种选择，要么把它拿到背包里，要么不把它放到背包里（这是建立在它的体积可以小于背包所剩体积的前提下），由于我们需要最大的重量，所以我们自然需要在这两种选择之间选择质量更大的，当然有可能背包根本放不下这个物品

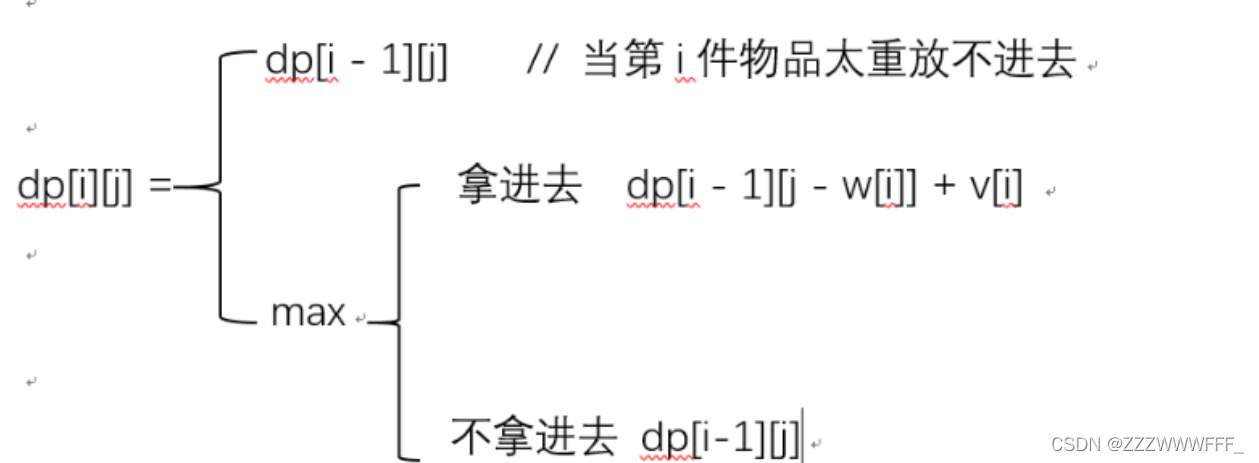
• 第三步即初始化数组dp，由于背包在没有放东西的时候质量为0，所以dp数组初始化为0即可?

代码转换如下：

class Solution {
public:
    int vw[1005][2];
    int dp[1005][1005] = { 0 };//定义dp[i][j]为只有前i个物品在j的背包体积下我们能获得的最大重量
    int knapsack(int V, int n, vector<vector<int> >& vw) {
	   for (int i = 1; i <= n; i++)//前i个物品 
	   {
		for (int j = 1; j <= V; j++)//背包体积 
		{
            if(j<vw[i-1][0])//背包放不下
            {
                dp[i][j]=dp[i-1][j];//状态不变
            }
            else
            {
				dp[i][j] = max(dp[i - 1][j - vw[i-1][0]] + vw[i-1][1], dp[i - 1][j]);           
            }拿或者不拿
		}
       }
	   return dp[n][V];
    }
};

?这里推荐另外一道相似的题目，感兴趣的同学可以看看采药 （动态规划）