[数据结构与算法]洛谷试炼场 普及组 动态规划的背包问题

相关视频：洛谷试炼场 普及组 动态规划的背包问题

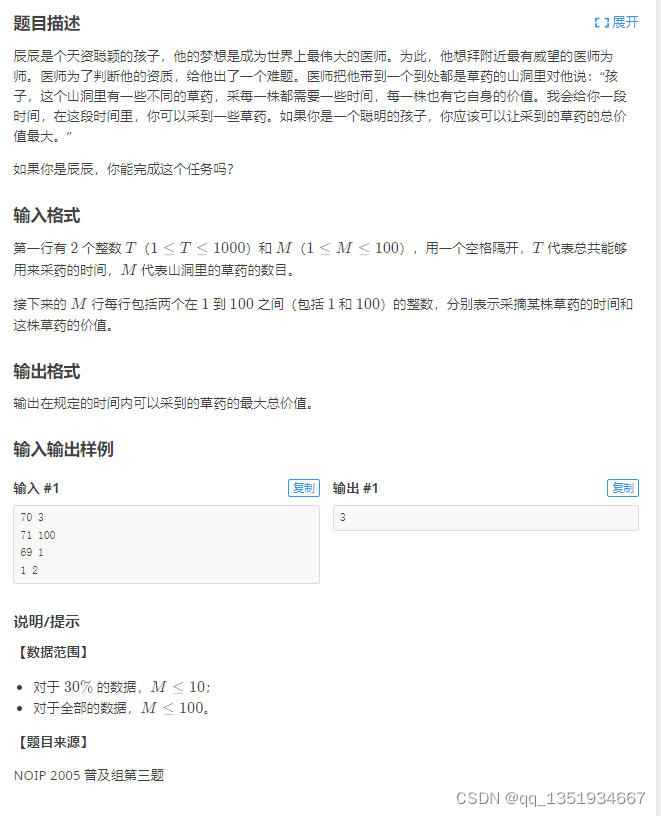
P1048 [NOIP2005 普及组] 采药

T就是背包的体积，M就是物品的数量，c[i]就是物品的体积，v[i] 就是物品的价值。

AC代码

#include<bits/stdc++.h>
using namespace std;
int T,M,c[105],v[105],dp[1005];
int  main()
{
	cin >> T >> M;
	for(int i=1;i<=M;i++)
		cin >> c[i] >> v[i];
	for(int i=1;i<=M;i++)
		for(int j=T;j>=c[i];j--)
			dp[j] = max( dp[j], dp[j-c[i]] + v[i]);
	cout << dp[T];
	return 0;
}

P1060 [NOIP2006 普及组] 开心的金明

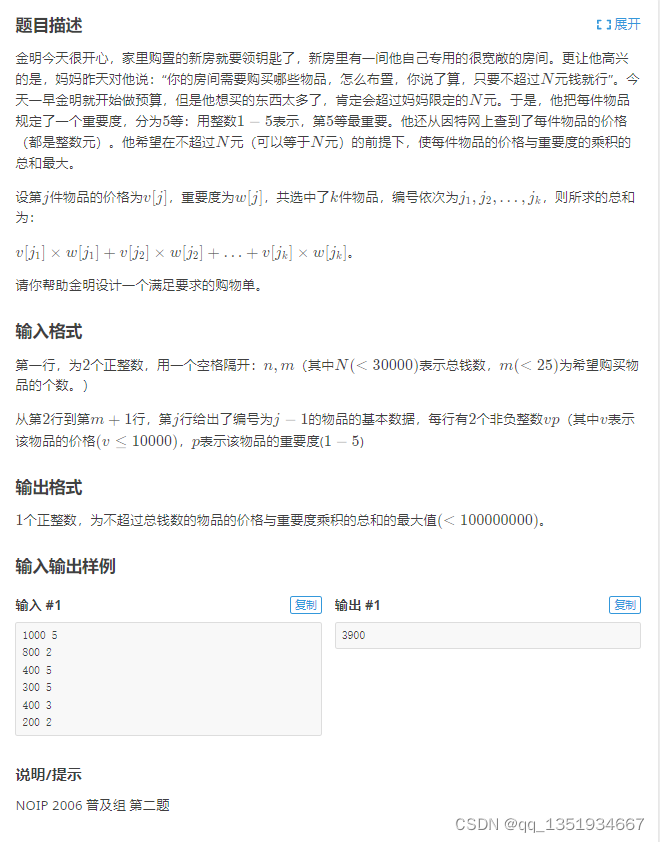
?这里物品的价值变成了价格与重要度乘积之和，所以需要更新一下

AC代码

#include<bits/stdc++.h>
using namespace std;
int N,M,c[30],v[30],dp[30005];
int  main()
{
	cin >> N >> M;
	for(int i=1;i<=M;i++)
	{
		cin >> c[i] >> v[i];
		v[i]=c[i]*v[i];
	}
	for(int i=1;i<=M;i++)
		for(int j=N ; j>=c[i];j--)
			dp[j] = max( dp[j], dp[j-c[i]] + v[i]);
	cout << dp[N];
	return 0;
}

P1049 [NOIP2001 普及组] 装箱问题

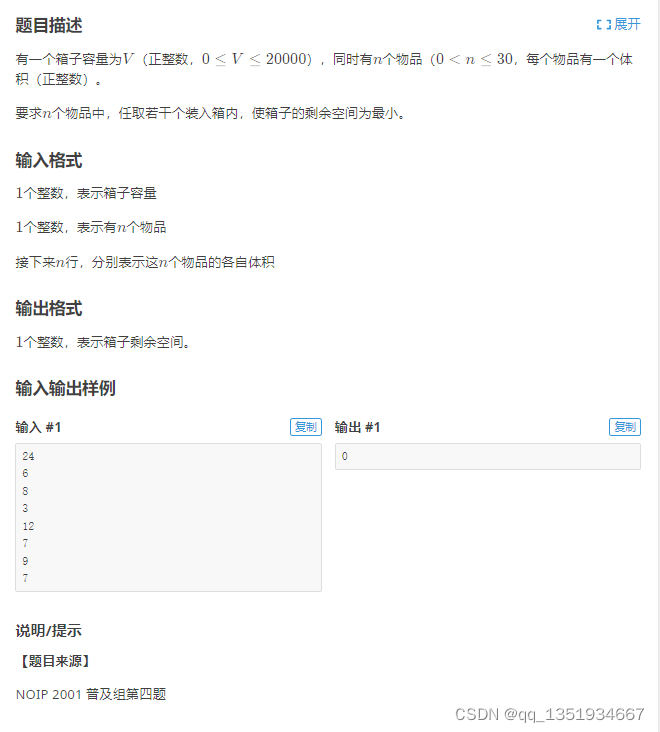
?没有体积，只有价值，此题物品的价值与体积一样

AC代码

#include<bits/stdc++.h>
using namespace std;
int N,M,c[35],v[35],dp[20005];
int  main()
{
	cin >> M >> N;
	for(int i=1;i<=N;i++)
	{
		cin >> c[i];
		v[i]=c[i];
	}
	for(int i=1;i<=N;i++)
		for(int j=M ; j>=c[i];j--)
			dp[j] = max( dp[j], dp[j-c[i]] + v[i]);
	cout << M-dp[M];
	return 0;
}

P1164 小A点菜

?此题同上题一样，物品的价值与体积一样，但此问题问的是有多少种方法？在初始状态下有不选这种方法，所以初始化时初始化为1，在核心代码那里只需累加每次方法即可。

此题和上题都是可以优化的，但我都没有优化，方便记忆模板，后续做此类01背包题都是直接套用模板。

AC代码

#include<bits/stdc++.h>
using namespace std;
int M,N,c[105],v[105],dp[10005]={1};
int  main()
{
	cin >> N >> M;
	for(int i=1;i<=N;i++)
	{
		cin >> c[i];
		v[i]=c[i];
	}
	for(int i=1;i<=N;i++)
		for(int j=M ; j>=c[i];j--)
			dp[j] += dp[j-c[i]];
	cout << dp[M];
	return 0;
}

P1734 最大约数和

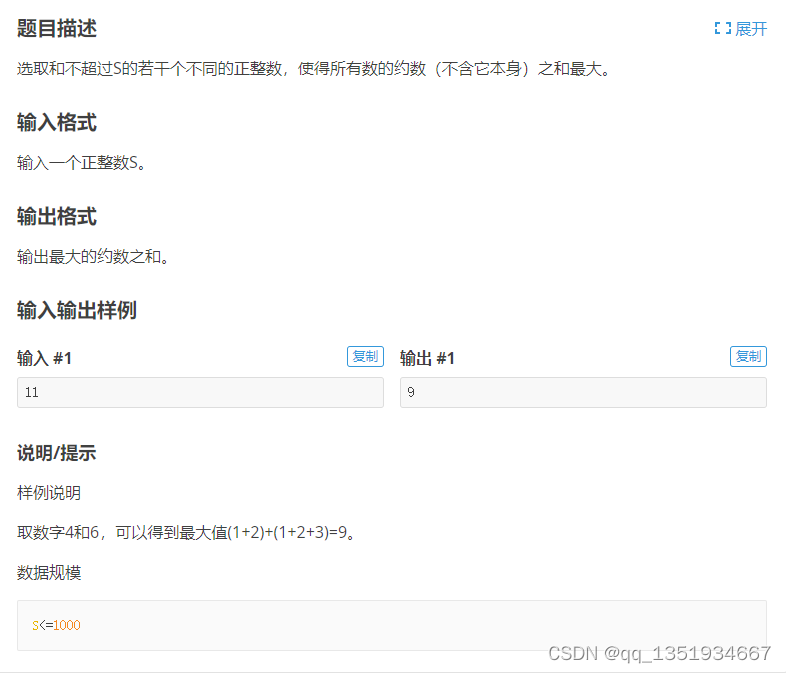
?这个题一眼看下不像01背包，深入一下，把他给的样例手写一下，就知道这是个01背包了，背包体积为S，背包数量也为S，物品体积就为1至S,物品价值就为这个物品的约数之和。

AC代码

#include<bits/stdc++.h>
using namespace std;
int N,M,c[1005],v[1005],dp[1005];
int  main()
{
	cin >> N;
	M=N;
	for(int i=1;i<N;i++)
	{
		c[i]=i;
		for(int j=1;j<i;j++)
			if(i%j==0)
				v[i]+=j;	
	}
	for(int i=1;i<=N;i++)
		for(int j=M ; j>=c[i];j--)
			dp[j] = max(dp[j],dp[j-c[i]]+v[i]);
	cout << dp[M];
	return 0;
}