[数据结构与算法]00动态规划中等 石子合并问题-合并金币

合并金币

描述

有 N 堆金币排成一排，第 i 堆中有 C[i] 块金币。每次合并都会将相邻的两堆金币合并为一堆，成本为这两堆金币块数之和。经过N-1次合并，最终将所有金币合并为一堆。请找出将金币合并为一堆的最低成本。

其中，1 <= N <= 30，1 <= C[i] <= 100
示例1
输入
4
3 2 4 1
输出
20

分析

参考：
"知性肥宅在线写bug"的（经典问题）—石子合并问题
"CHENG Jian"的石子合并问题–动态规划;贪心

dp[i][j]表示第i堆到第j堆之间合并的最小代价。
动态规划方程是：

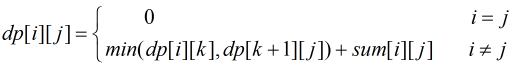
min(dp[i][k],dp[k+1][j])只是i，j之间，两个堆合并成为一个堆的代价，并没有考虑得到这两个堆的合并代价。所以要加上第i堆到第j堆之间的总和，才是dp[i][j]。

import java.util.Scanner;
public class Main{
    public static void main(String[] args){
        Scanner scan = new Scanner(System.in);
        int n = scan.nextInt();
        int[] nums = new int[n];
        for(int i = 0; i < n; i++){
            nums[i] = scan.nextInt();
        }
        int[][] dp = new int[n][n];
        int[][] sum = new int[n][n];
        for(int i = 0; i < n; i++){
            for(int j = i; j < n; j++){
                if(i == j){
                    sum[i][j] = nums[i];
                    continue;
                }
                sum[i][j] = sum[i][j-1] + nums[j];
            }
        }
        for(int i = n - 1; i >= 0; i--){
            for(int j = i + 1; j < n; j++){
                int min = Integer.MAX_VALUE;
                for(int k = i; k < j; k++){
                    if(dp[i][k] + dp[k+1][j] < min){
                        min = dp[i][k] + dp[k+1][j];
                    }
                }
                dp[i][j] = min + sum[i][j];
            }
        }
        System.out.println(dp[0][n-1]);
    }
}