????????欢迎来到老胡的算法解题思路,本文章主要使用的语言为java,使用的题型为力扣算法题,基于这一篇文章,我将为你介绍栈和队列的基础知识和栈和队列的题型,喜欢的朋友可以关注一下,下次更新不迷路!
????????栈和队列是一组有序列表,是功能受限的线性表结构,可以用数组或链表来实现,队列数据存取先入先出,栈先入后出。队列是基于地址指针进行遍历,从头部或尾部进行遍历,不需要开辟空间,因为在遍历的过程中数据结构不受影响。栈只能从顶部取数据,也就是说最先进入栈底的,需要遍历整个栈才能取出来,需要遍历数据时需要开辟临时空间,保持数据在遍历前的一致性。
一、栈和队列的常用方法
//栈Stack
push()//入栈
empty()//栈空返回真,否则为假
peek()//获取栈顶值,不出栈
pop()//获取栈顶值,出栈
get()//获得栈中对应值
//队列Queue和优先队列PriorityQueue
add()//入队
offer()//将指定元素插入队列,成功返回true,否则返回false
peek()//获取队头的值,但不出队
poll()//获取并移除队头
remove()//获取并移除队头
//双向队列Deque
addFirst()//从队列头部插入数据
addLast()//从队列尾部插入数据
removeFirst()//从队列头部删除数据
removeLast()//从队列尾部删除数据
pollFirst()//获取并移除队头
pollLast()//获取并移除队尾
peekFirst()//获取队头的值,但不出队
peekLast()//获取队头的值,但不出队二、栈和队列题型
2.1、栈和队列的相互实现
例题:力扣225.用队列实现栈
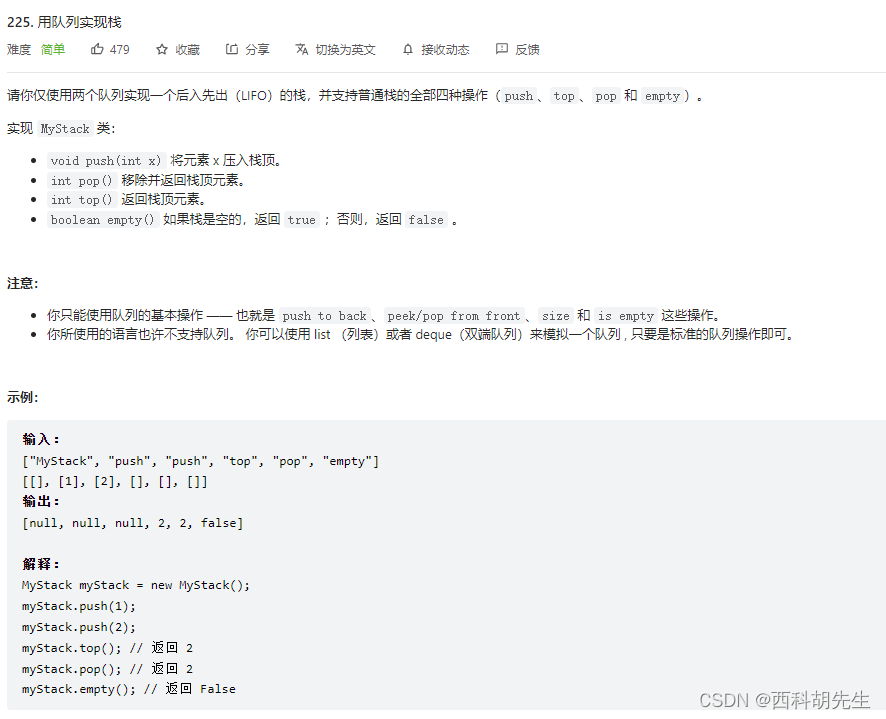
?分析:题目分析
针对这道题,队列实现栈,注意栈的定义,先进后出,再想想队列的种类,这个题直接使用双向队列就可以解题。反过来,如果遇到栈实现队列,可以选用两个栈来处理,一个存储数据,一个进行数据间的转换。这里,为啥选取这个题,一来是为了让初学者更好的理解栈和队列,同时也为了让初学者理解双向队列,在以后遇到栈的问题,可以用双向队列来实现。
解题:完整代码
class MyStack {
// 声明双向队列
Deque<Integer> deque;
public MyStack() {
deque = new LinkedList<Integer>();
}
// 将元素压入栈顶
public void push(int x) {
deque.addFirst(x);
}
// 移除并返回栈顶元素
public int pop() {
return deque.removeFirst();
}
// 返回栈顶元素
public int top() {
return deque.peekFirst();
}
// 判断是否为空
public boolean empty() {
return deque.isEmpty();
}
}
2.2、括号类题型
例题:力扣921.使括号有效的最少添加
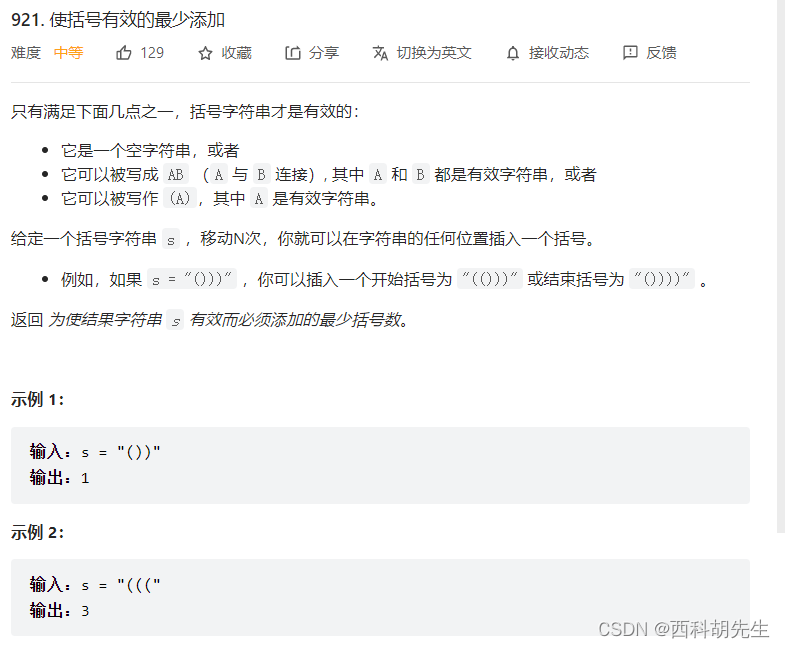
?分析:题目分析
????????针对这类题型,可以使用栈来解题,采取遇到左括号就?栈,遇到右括号就去栈中寻找最近的左括号,看是否匹配的策略
分析:解题模板
boolean isValid(String str) {
// 声明字符类型的栈
Stack<Character> stack = new Stack<>();
// 字符串转数组直接遍历,也可用其他便利方法
char[] str1 = str.toCharArray();
for (char ch : str1) {
// 左括号入栈,右括号出栈
if (ch == '(' || ch == '{' || ch == '[')
stack.push(ch);
else {
if (!stack.empty() && transform(ch) == stack.peek())
stack.pop();
else
return false;
}
}
// 栈为空,匹配成功,反之则不成功
return stack.empty();
// 字符转换函数
}char transform(char ch) {
if (ch == '}') return '{';
if (ch == ')') return '(';
return '[';
}解题:完整代码
class Solution {
public int minAddToMakeValid(String S) {
int ans=0;
// 构建栈
Stack<Character> stack=new Stack<>();
for(int i=0;i<S.length();i++){
// 匹配字符
if(S.charAt(i)=='('){
// 入栈
stack.push('(');
}
else if(stack.isEmpty()){
ans++;
}
else{
stack.pop();
}
}
return ans+stack.size();
}
}2.3、找元素问题
例题:力扣556.下一个更大元素|||
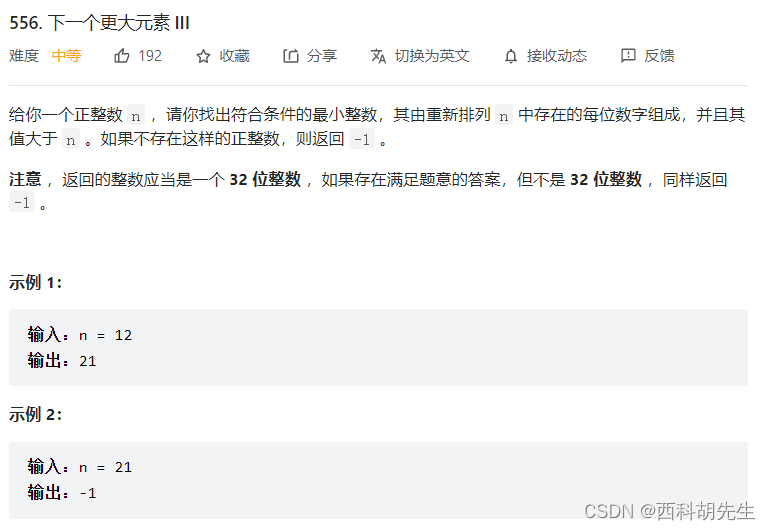
?分析:题目分析
? ? ? ? 对于这一类题型,可以直接暴力解,但是暴力的话时间复杂度太高,可以考虑采用优先队列的方式,让他们的值排序,然后就选取出稍微比当前位大一点的数,后面的直接用排列的最小数就可以还原。当然了,还要注意判断数据是否溢出。
解题:完整代码
class Solution {
public int nextGreaterElement(int n) {
//优先队列
PriorityQueue<Integer> priorityQueue = new PriorityQueue<>();
// 计数,*10后用于n数据的还原
int count1 = 1;
//判断开关,防止多次条件成功
int count2 = 0;
//存储低一位的数
int count=Integer.MIN_VALUE;
while(n!=0){
int num = n%10;
//对应后面的数据还原
n = n/10;
// 进入队列
priorityQueue.add(num);
//判断后一位数和前一位,看是否满足关系
if(count>num){
n=n*10;
while(!priorityQueue.isEmpty()){
// 出队列
int num1 = priorityQueue.poll();
if(count2==0&&num<num1){
count2 = 1;
//判断是否溢出
if(n>Integer.MAX_VALUE/10 || (n==Integer.MAX_VALUE/10&&num1>7)){
return -1;
}
// 数值还原
n = n+num1*count1;
}
else{
// 判断是否溢出
if(n>Integer.MAX_VALUE/10 || (n==Integer.MAX_VALUE/10&&num1>7)){
return -1;
}
count1*=10;
// 数值还原
n = n*10+num1;
}
}
return n;
}
// 后一位数更新
count = num;
}
return -1;
}
}2.4、数组去重
例题:力扣316.去除重复字母

?分析:题目分析
? ? ? ? 关于去重算法,给我们的第一反应,直接用哈希表解决就可以了,但是看到这类比较复杂的去重,有不知道从何下手。如果我们想要有序的结果,那就得对原字符串排序,排序后再去重,但是排序后就不得不打乱其他字符的位置了,这显然解法是错误的,针对这种题型,我们可以考虑用单调栈来解,先用一个数组标记每个元素重复的此时,在通过元素和栈顶元素的比较以及元素出现的次数是否满足条件来阶梯。
解题:完整代码
class Solution {
public String removeDuplicateLetters(String s) {
int[] ans = new int[26];
for (int i = 0; i < s.length(); i++) {
// 给ans数组赋值,记录每个元素出现的次数
ans[s.charAt(i) - 'a']++;
}
// 单调栈初始化
Stack<Character> stack = new Stack<>();
for (int i = 0; i < s.length(); i++) {
char ch = s.charAt(i);
// 如果栈中已经存在该元素,数组对应出现次数减一
if (stack.contains(ch)){
ans[ch - 'a']--;
continue;
}
// 如果栈非空并且栈顶元素字典值大并且栈顶值出现不止一次
while (!stack.isEmpty() && stack.peek() > ch && ans[stack.peek() - 'a'] > 1){
// 移除该元素并且对应的出现次数减一
char ch1 = stack.pop();
ans[ch1 - 'a']--;
}
// 入栈
stack.push(ch);
}
// 合成字符串答案
String answer = "";
for (int i = 0; i < stack.size(); i++) {
answer+=stack.get(i);
}
return answer;
}
}2.5、最大面积
例题:力扣84.柱状图中最大的矩形

分析:题目分析
? ? ? ? 对于这一类题型,可以直接暴力解,但是暴力的话时间复杂度太高,同时容易出错,也可以使用动态规划来解,方法不唯一,但在这,我介绍的是用单调栈来解。解题时先通过单调栈寻找到比上一个元素小的值,求出这个值对应的最大面积 ,同时通过进栈和出栈使得栈里面元素单调,在通过这个栈求解对应的最大面积,两者相比即可。
解题:完整代码
class Solution {
public int largestRectangleArea(int[] heights) {
int len = heights.length;
// 初始化高度和宽度
int height = 0;
int width = 0;
int area=0;
int num = 0;
// 初始化单调栈
Stack<Integer> stack = new Stack<>();
for(int i=0;i<len;i++) {
// 右边高度小于左边高度且栈不为空时,通过while解出当前位置能得到的最大面积
while (!stack.isEmpty() && heights[i] < heights[stack.peek()]) {
// 移除栈顶元素,并根据这个值找到对应高度
num = stack.pop();
height=heights[num];
// 根据栈得出对应宽度
if(!stack.isEmpty()){
width=i-stack.peek()-1;
}else{
width = i;
}
// 得出最大面积
area=Math.max(area,height*width);
}
// 如果栈为空或者下一个高度大于上一个高度,入栈
stack.push(i);
}
// 正面扫描完毕,逆向继续扫描
while (!stack.isEmpty()) {
// 移除栈顶元素,并根据这个值找到对应高度
num = stack.pop();
height=heights[num];
// 根据栈得出对应宽度
if(!stack.isEmpty()){
width=len-1-stack.peek();
}else{
width=len;
}
// 求出最大面积
area = Math.max(area,height*width);
}
return area;
}
}三、总结
? ? ? ? 栈和队列是功能受限的线性表结构,在实际的算法解题中,不推荐使用栈,因为栈继承了Vector,同时栈中是用了大量的synchronized修饰,虽然线程安全,但是效率大打折扣,推荐使用队列中的双向队列Deque来实现栈的基本操作。
????????补充说明:栈和队列还存在很多没有总结到的典型题型,后期总结后继续补上