1.朴素算法
主要包含两个部分,打个比方:
主串:整个百度出来的结果
子串:我们输入的数据

我们如何将我们子串的内容与我们主串的内容进行相互匹配呢?
我们来进行一个案例测试下:
S = “alibabaalimama”
T = “alimama”
我们进行模式匹配的时候,有一种方式叫做朴素匹配方式(BF)我们先用这种方式来进行匹配,但是这种匹配方式,效率不是很高,于是我们之后就引入了KMP算法的样例,在朴素匹配的基础上进行匹配:

朴素匹配算法核心,也是进行一步一步遍历所得到,他用的主要是两个for循环。如下代码:
for (i=0;i<m;i++)
for(j=0;j<n;j++)
两个for循环,会在开始的位置,慢慢遍历,当我们第一次i=4,j=4的时候,出现了不相同,于是我们的外层循环j++,进入下一步循环。当我们i=2,j=1的时候,出现了不相同的串,于是我们继续执行外层循环的j++,然后依次迭代下去,直到最后,遍历到i=9,j=1的时候,我们循环全部的结果之后,发现,字符串,全部匹配,此时我们就返回结果。
以上的这种方式,比较暴力,进行的比较慢,主要核心思想就是当子串和主串不匹配的时候,子串往下移动一个.时间复杂度为O(n*m)。这种方式是比较鸡肋的。所以引入了我们下面的这种kmp算法的方式来计算,能够大大提高了效率。
缺点是:不太能够智能,每次都是一个一个的往后面移动,然后进行遍历对比,有些时候,我们匹配过的位置,是不需要重新迭代的,但是朴素算法,依旧会从头开始迭代。
我们发现,i和j标注的是它不匹配时候的位置,于是我们可以想象下,是否,下次我们可以从这个不匹配的位置开始执行呢,而不是从头开始。
2.kmp算法
kmp算法就是对应的朴素算法的一种改进方式:
核心思路就是求我们需要的next数组,而next数组针对的是子串而言的。
next数组,又分为几种情况;如下图所示

我们找出子串

通过给出的字符串,来计算他的next数组

由于我们计算的单引号字符串,因此它的下标是从1开始的,我们开始对照公式来计算。当编号为1 的时候,对照公示,公式,他的next数组中对用的值为0。当编号为2时,我们把当前编号2后面的所有串都去除掉,此时我们只剩下一个a,对应的a是没有构成一个对称关系的 ,因此,在我们公式中,是属于其他情况,因此对应b的next数组值为1。此时我们遍历到编号为3的时候,我们将3与后面所有的串都删除,此时只保留了ab,ab仍旧是不存在对称关系的,于是我们对应编号3的他的next数组值也仍旧为1。

当我们遍历到编号为4的时候,我们将编号4和之后的所有串都去除,此时只剩下“aba”,aba存在着一个对称关系。对于中间b,a成对称关系。此时我们的编号需要加1.那么对应的编号4他的next数组的值是2。
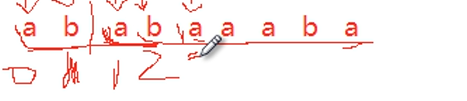
当我们遍历到5编号是,将5和之后的所有元素都去除,然后此时只剩下”abab”,我们发现左边的ab与右侧的ab存在着某种对称关系,此时,我们计算next数组,那么对应的编号5的next数组值即为上一个元素值加1.即为3。

当我们遍历到编号6的时候,将6个之后所有元素都去除,然后此时只剩下”ababa”,我们发现,左侧”aba”与右侧的”aba”存在着某种对称关系,因此在我们计算next数组的时候,发现是3个元素存在对称关系,因为我们的next数组值为4;

当我们遍历到编号7的时候,将7编号之后的所有元素都去除,然后此时只剩下,”ababaa”此时我们发现,收尾两个”a“存在某种对称关系,将中间“baba“当做对称轴,此时存在一个a的对称关系,那么next数组的下标即为2.

当我们遍历到编号8的时候,将8编号之后所有的元素都去除,然后此时只剩下。”ababaaa”,我们发现此时和上述情况类似,因此,他的next数组值也为2

当我们遍历到编号9的时候,将9之后所有元素都去除,然后此时只剩下,”ababaaab”此时我们发现首尾元素”ab”存在着某种对称关系。因此,我们对应的9编号的next数组值为3.此时我们已经全部计算出了,我们整个串的next数组。

此时我们用另外一个串来验证我们的计算方式:用我们找某种对称关系的方式来进行求解next数组。从某个地方开始划线,切割之后看是否重合,想尽办法进行切割,找到最大重合(收尾重合)
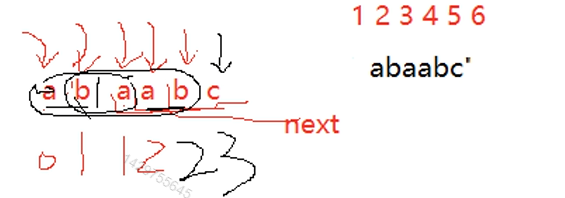
总结一下上面计算方式的口诀:
切两次:(相尽办法去切割,)
第一次:取前面的
第二次:(重新切)取后面的
如果两者重合,那么MAX就是字符数+1。
此时我们通过一个题目来计算验证下我们的方式:

依据刚刚方式,我们已经计算出了,子串的next数组,为[-1,0,0,1,1,2]
在kmp算法中,i是不会变小的。
我们进行实际匹配操作

第一次失配的时候,i=5.j=5,对照着next数组计算之后,我们可以得到,i=5,j=2.那么我们主串下标为5的字符和子串下标为2的字符进行对照。如下图

此时在位置i=8,j=5的时候,主串和子串再次失配,因此,对照着next数组,我们可以得到。i=8,j=2.将主串下标为8的字符,和子串下标为2 的字符进行位置匹配。
此时依次,计算,最终即可得到我们想要的结果。
总结:
KMP算法的核心是计算子串的next数组,然后通过计算的next数组,来进行位置匹配,通过计算的j的位置,去next数组中去寻找我们对应的位置,然后由于在next数组中。i是不会变小的。依次遍历。因此这样大幅度提高了,我们遍历的效率。它的时间复杂度为O()m+n)
可能以上描述太过于口语化,具体想了解如何计算的,可以私信我。
过计算的j的位置,去next数组中去寻找我们对应的位置,然后由于在next数组中。i是不会变小的。依次遍历。因此这样大幅度提高了,我们遍历的效率。它的时间复杂度为O()m+n)
可能以上描述太过于口语化,具体想了解如何计算的,可以私信我。