leetcode 95：不同的二叉搜索树

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同 二叉搜索树 。可以按 任意顺序 返回答案。

示例 1：

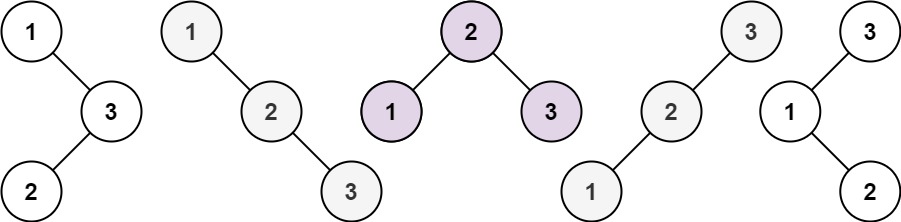
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例 2：

输入：n = 1
输出：[[1]]

提示：

1 <= n <= 8

思路：回溯

分析：对于1-n这个n个数来说，都有可能做二叉搜索树的根节点，显然，我们需要把这n个数都遍历一遍。设f(1,n)表示[1,n]构成的二叉搜索树。

假设当x作为根节点时，那么左子树的数值范围是[1,x-1]，右子树的数值范围是[x+1,n]。显然，左子树和右子树放到f函数里面成立。可以使用递归解决这个问题。
我们遍历一个节点作为根节点，然后根据递归返回它的可能的左右子树的集合。举例：当左子树的可能性有2种，右子树的可能性有3种，那么这棵树有2*3种可能性，也就是笛卡尔积。

因为返回的集合长度为0，需要对叶子节点，只有左孩子的节点、只有右孩子的节点，单独判断下。

class Solution {

    public List<TreeNode> generateTrees(int n) {
        return inOrder(1,n);
    }
    public List<TreeNode> inOrder(int left,int right){
        List<TreeNode> lists = new ArrayList<>();
        //递归结束
        if(right < left){
            return lists;
        }
        for(int i = left; i <= right;i++){

            //找到左子树各种可能性的集合
            List<TreeNode> leftList = inOrder(left,i-1);
            //找到左子树各种可能性的集合
            List<TreeNode> rightList = inOrder(i+1,right);
            //将左子树和右子树的集合 根据笛卡尔积 和根节点生成不同的树
            //没有左右孩子
            if(leftList.size() == 0 && rightList.size() == 0){
                lists.add(new TreeNode(i));
                //只有右孩子
            }else if(leftList.size() == 0){
                for (TreeNode node : rightList) {
                    TreeNode root = new TreeNode(i);
                    root.right = node;
                    lists.add(root);
                }
                //只有左孩子
            }else if(rightList.size() == 0){
                for (TreeNode node : leftList) {
                    TreeNode root = new TreeNode(i);
                    root.left = node;
                    lists.add(root);
                }
                //左右孩子都有 生成孩子的笛卡尔积
            }else{
                for(int j = 0 ; j < leftList.size();j++){

                    for(int k = 0 ; k < rightList.size();k++){
                        //创建根节点
                        TreeNode root = new TreeNode(i);
                        root.left = leftList.get(j);
                        root.right = rightList.get(k);
                        lists.add(root);
                    }
                }
            }
        }
        return lists;
    }
}
解答成功:
			执行耗时:1 ms,击败了98.32% 的Java用户
			内存消耗:41.1 MB,击败了72.69% 的Java用户

改进：

参考leetcode：当节点不存在的时候，可以往集合中添加一个null，这样就不需要区分叶子、只有左孩子的节点、只有右孩子的节点，这三种可能性了。

class Solution {

    public List<TreeNode> generateTrees(int n) {
        return inOrder(1,n);
    }
    public List<TreeNode> inOrder(int left,int right){
        List<TreeNode> lists = new ArrayList<>();
        //递归结束
        if(right < left){
            lists.add(null);
            return lists;
        }
        for(int i = left; i <= right;i++){

            //找到左子树各种可能性的集合
            List<TreeNode> leftList = inOrder(left,i-1);
            //找到左子树各种可能性的集合
            List<TreeNode> rightList = inOrder(i+1,right);
            //将左子树和右子树的集合和根节点 根据笛卡尔积生成不同的树
            for(int j = 0 ; j < leftList.size();j++){
                for(int k = 0 ; k < rightList.size();k++){
                    //创建根节点
                    TreeNode root = new TreeNode(i);
                    root.left = leftList.get(j);
                    root.right = rightList.get(k);
                    lists.add(root);
                }
            }
        }
        return lists;
    }
}
解答成功:
			执行耗时:1 ms,击败了98.32% 的Java用户
			内存消耗:41.9 MB,击败了38.47% 的Java用户