[数据结构与算法]WS小世界网络的仿真实现

🎀前言

1998年Watts和Strogatz在Nature上发表了题为《“小世界”网络的群体动力行为》，提出了小世界网络模型。在小世界网络中，其各节点之间的连接状况（度数）具有均匀分布性，网络中大部分的结点不与彼此邻接，但大部分结点可以从任一其他点经少数几步就可到达。若将一个小世界网络中的点代表一个人，而连结线代表人与人认识，则这小世界网络可以反映陌生人由彼此共同认识的人而连结的小世界现象。

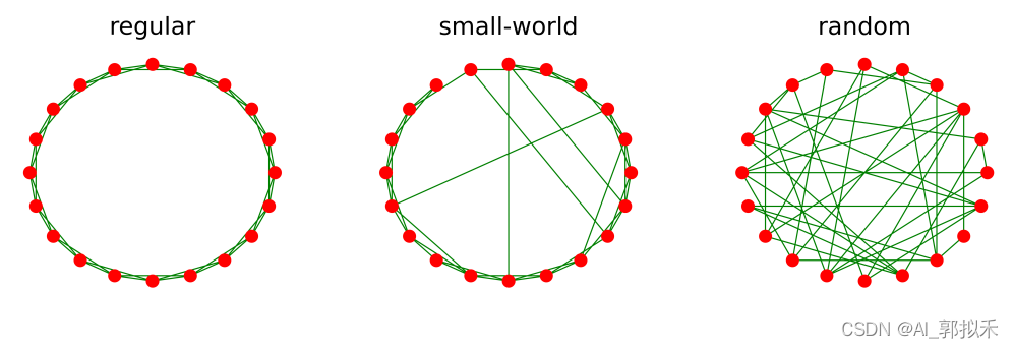
小世界网络是一种介于规则网络和随机网络中的特殊网络。

🌂MATLAB代码

clc, clear, hold on
N = 5000; K = 4; p = 0.1; %N为网络节点总数，K为邻域节点个数，p为重连概率
t = 0:2*pi/N:2*pi-2*pi/N;  %生成最近邻耦合网络各节点坐标的参数方程的角度
x = 100*sin(t); y=100*cos(t);
plot(x,y,'ro','MarkerEdgeColor','g','MarkerFaceColor','r','markersize',6);
A=zeros(N);    %邻接矩阵初始化
for i=1:N      %该层循环构造最近邻K耦合网络的邻接矩阵
   for j=i+1:i+K/2
       jj=(j<=N)*j+(j>N)*mod(j,N); %如果j超过了N，要取除以N的余数
       A(i,jj)=1; A(jj,i)=1;
   end
end
for i= 1:N    %该层循环进行随机重连
   for j=i+1:i+K/2
       jj=(j<=N)*j+(j>N)*mod(j,N); 
       ChangeV=randi([1,N]); %产生随机整数，为可能重连的另外一个节点
       if rand<=p & A(i,ChangeV)==0 & i~=ChangeV  %重连的条件
          A(i,jj) = 0; A(jj,i) = 0; %删除原边
          A(i,ChangeV)=1; A(ChangeV,i)=1;  %重连新边
       end
   end
end
for i=1:N-1 
    for j=i+1:N
        if A(i,j)~=0
            plot([x(i),x(j)],[y(i),y(j)],'linewidth',1.2); 
        end
    end
end
%把邻接矩阵A转换为Pajek格式的数据，
%这里函数Matlab_to_Pajek是我们自己编写的函数。
Matlab_to_Pajek(A); 

🍔数据保存函数（用于分析、可视化等）

function Matlab_to_Pajek(A,k)  
%Matlab邻接矩阵A转换成Pajek数据的函数
%k是第k次转换，生成的文件命名成Pajek_datak.net,
%如果不输入第2个参数k,默认文件名为Pajek_data1.net
if nargin==1
    str='Pajek_data1.net';
else
    str=['Pajek_data',int2str(k),'.net'];
end
n=length(A); v=1:n;
fid=fopen(str,'w');  %创建纯文本文件Pajek_data.net
fprintf(fid,'%s%d\n','*Vertices  ',n); %写入字符串并换行
for i=1:n
   fprintf(fid,' %d  ',v(i));   %写入节点编号
   fprintf(fid,'"%d"\n',v(i));  %写入双引号节点字符串并换行
end
fprintf(fid,'%s\n%s\n','*Arcs','*Edges'); %写入两个字符串并各自换行
A=tril(A);  %截取邻接矩阵的下三角元素
[u,v]=find(A); n=length(u); %找非零元素，并计算个数
for i=1:n
    fprintf(fid,'  %d  %d  1\n',u(i),v(i));  %逐条边写入信息并换行
end
fclose(fid);