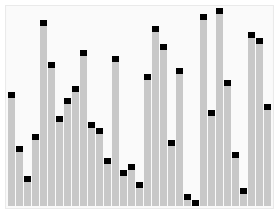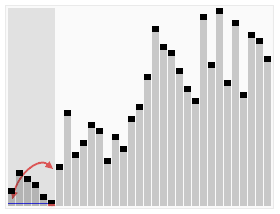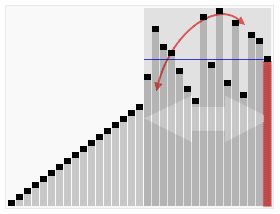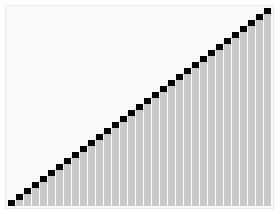
做题时经常会遇到直接或变相找第几大或第几小的问题,提供一个模板:即利用对快速排序的改造快速找到第k大/小的数;
先简单说一下快排的原理(会的直接跳过):分区。即挑出一个基准数,将比这个数小的数放在前面,比这个数大的数放在后面。这样完成一次分区。经过不断的分区来使每个数放到它该去的地方。详见两个博客:快速排序原理?;单循环完成快速排序(后面这个是我用的快排)
快排的动图展示
?
?再说说如何应用:
要找第k大的数,大多数人会选择先排好序再从后往前标记着寻找,但这样对于一些数据较大的题很容易时间超限,那么,利用快排的特性边排边找,就会快许多(快排本身就很快)。
目标是:在进行一次分区后,判断当前分区后的基准值是否为目标的第k大-1(数组从0开始),如果是,返回数组在基准处储存的值,不是的话,判断该基准对应的排序位置是比k-1大还是k-1小,如果比k-1大,证明要找的值在左边,那么只排左边就可以了,否则排右边。
目标已经明确了,再看看这个寻找函数需要引用什么值:
由于快排的特性,需要引入左边界l与右边界r,出于自身需要又需要引入目标排序值rank;如果想写一个比较通用的函数,即在不同的题目中都能调用,那么还需要引入目标数组target?
看看寻找函数的代码:?
int findk(int target[], int rank, int l, int r) {//目标数组,目标排名,左边界,右边界 if (l < r) {//快速排序成立条件,左边界小于右边界 int p = l;//设置最初基准(一般设置为左边界) int index = p + 1;//这里之后在《单循环完成快速排序》里写的有,就不过多赘述了 for (int i = index; i < r; i++) { if (target[i] > target[p]) {//如果要找第rank小的数,把>换成<就可以了 int t = target[i]; target[i] = target[index]; target[index] = t; index++; } } int t = target[p]; target[p] = target[index - 1]; target[index - 1] = t; p = index - 1; if (p == rank - 1) return target[p];//如果排到第rank大,返回该位置的值 else if (p > rank - 1) return findk(target, rank, l, p);//值较大,向左找(p是因为数组从0开始) else return findk(target, rank, p + 1, r);//否则向右找 } }
从n个数中找第k大的数? 先输入n,再输入n个数,再输入k
完整代码 :
#pragma GCC optimize(2)//O(2)优化,可以不写
#define _CRT_SECURE_NO_WARNINGS//防止VS对scanf和printf等报错,不用VS可以不写
#include<bits/stdc++.h>//万能头,c语言换成普通的头文件就可以了
#define endl '\n'//不用管
using namespace std;//不用管
int a[1000001];//目标数组
inline int int_read() {//快读,读取速度较快,csdn可以搜模板
char ch = getchar();
int x = 0, f = 1;
while (ch > '9' || ch < '0') {
if (ch == '-') f = -1;
ch = getchar();
}
while (ch <= '9' && ch >= '0') {
x = x * 10 + ch - '0';
ch = getchar();
}
return x * f;
}
int findk(int target[], int rank, int l, int r) {//目标数组,目标排名,左边界,右边界
if (l < r) {//快速排序成立条件,左边界小于右边界
int p = l;//设置最初基准(一般设置为左边界)
int index = p + 1;//这里之后在《单循环完成快速排序》里写的有,就不过多赘述了
for (int i = index; i < r; i++) {
if (target[i] > target[p]) {//如果要找第rank小的数,把>换成<就可以了
int t = target[i];
target[i] = target[index];
target[index] = t;
index++;
}
}
int t = target[p];
target[p] = target[index - 1];
target[index - 1] = t;
p = index - 1;
if (p == rank - 1) return target[p];//如果排到第rank大,返回该位置的值
else if (p > rank - 1) return findk(target, rank, l, p);//值较大,向左找(p是因为数组从0开始)
else return findk(target, rank, p + 1, r);//否则向右找
}
}
int main() {
ios::sync_with_stdio(false); cin.tie(0);//不用管
int n, rank;
n = int_read(); //读入n
for (int i = 0; i < n; i++) {
a[i] = int_read();//读入数据
}
rank = int_read();//读入k
printf("%d", findk(a, rank, 0, n));//输出
return 0;
}?