题目描述

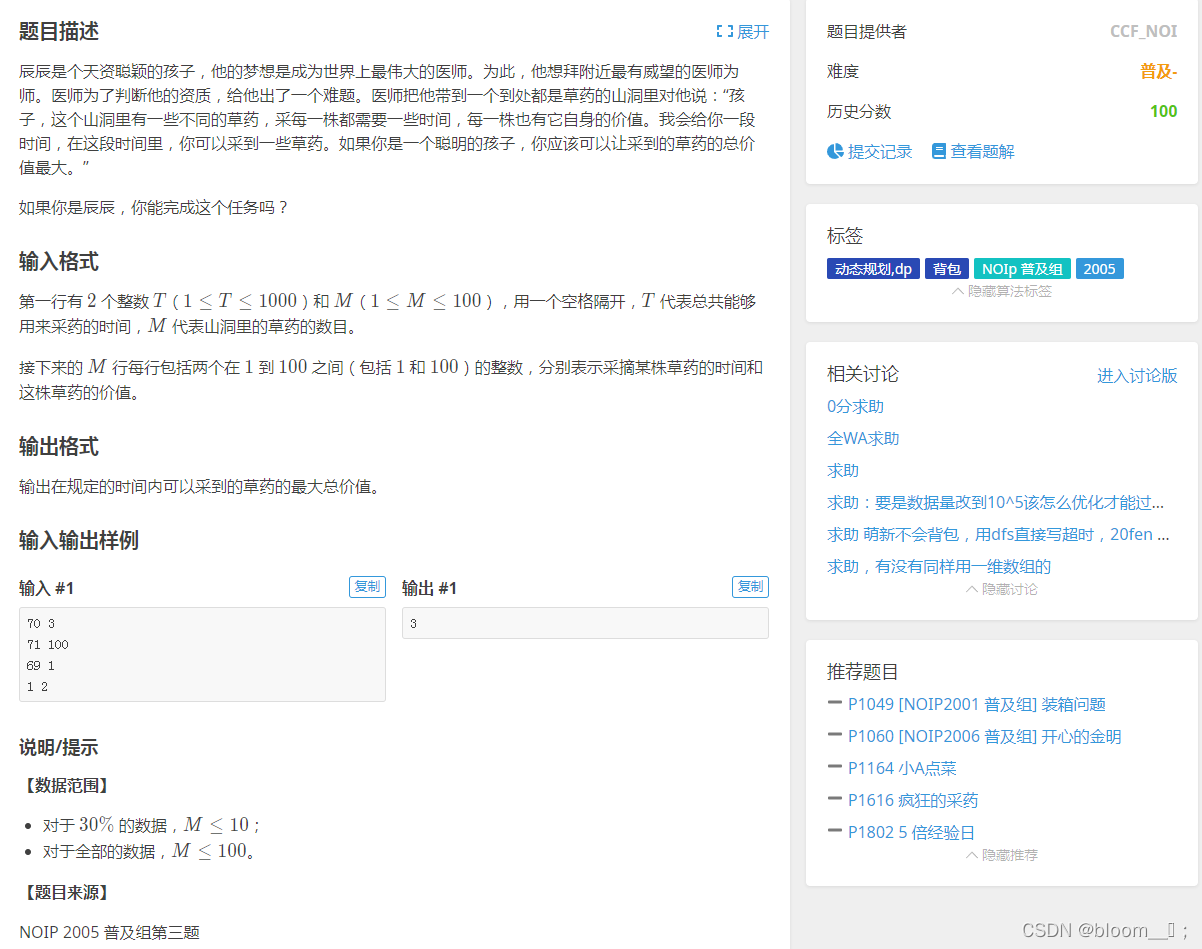
在这里插入图片描述

方法一、记忆化搜索

思路

对于每个药材，都有选与不选两种选择，最直接的方法就是使用dfs暴搜每种情况，但是提交会超时，所以在此基础上进行改进。
定义一个二维数组memo，memo[i][j] 表示在时间 j 内采前 i 个药材的最大价值。
采用自定向下的方式进行搜索：
对于两种选择：
----选：当前药材的价值 + 前时间 j 内 i - 1个药材的最大价值
----不选：前时间 j 内 i - 1个药材的最大价值
得到状态转移方程：memo[i][j] = max(memo[i - 1][j], memo[i - 1][j - cost[i]] + value[i])

将memo全部初始化为-1，当memo[i][j] 不等于-1时直接返回

代码

import java.util.Arrays;
import java.util.Scanner;

public class Main {

    static int[] cost = new int[105];
    static int[] value = new int[105];
    static int[][] memo = new int[105][1005];
    static int T, M;

    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        T = scan.nextInt();
        M = scan.nextInt();
        for (int[] a : memo) {
            Arrays.fill(a, -1);
        }
        for (int i = 1; i <= M; i++) {
            cost[i] = scan.nextInt();
            value[i] = scan.nextInt();
        }
        int ans = dfs(M, T);
        System.out.println(ans);
    }

    private static int dfs(int m, int t) {
        if (m == 0 || t == 0) return memo[m][t] = 0;
        if (memo[m][t] != -1) return memo[m][t];
        int c1 = dfs(m - 1, t);
        int c2 = -Integer.MAX_VALUE;
        if (t >= cost[m]) c2 = value[m] + dfs(m - 1, t - cost[m]);
        memo[m][t] = Math.max(c1, c2);
        return memo[m][t];
    }
}

方法二、动态规划（01背包）

思路

这道题算是01背包的模板题。
将时间看做背包容量，
将药材看做物品，
将药材采摘需要的时间看做物品重量，
将药材的价值看做物品价值，
最后直接套01背包模板

代码

import java.util.Scanner;

public class Main {
    public static void main(String[] args) {
        Scanner scan = new Scanner(System.in);
        int T = scan.nextInt(), M = scan.nextInt();
        int[] cost = new int[M], value = new int[M];
        for (int i = 0; i < M; i++) {
            cost[i] = scan.nextInt();
            value[i] = scan.nextInt();
        }
        int[] dp = new int[T + 1];
        for (int i = 0; i < M; i++) {
            for (int j = T; j >= cost[i]; j--) {
                dp[j] = Math.max(dp[j], dp[j - cost[i]] + value[i]);
            }
        }
        System.out.println(dp[T]);
    }
}