一.堆排序
堆排序:采用近似完全二叉树(堆)的数据结构的排序算法。
二叉树:结合树的生长,会不断地进行一分为二。
结合图文解析:
1.最顶端是父节点,左分支是左节点,右分支是右节点。
2.左右分支都可以被称为子节点。
3.用数组存储大顶堆:数组下标从0开始,堆的顺序从最大值开始。
4.假设下标为i,得到下列的公式:
???父节点下标 : (i-1)/2
???左节点(孩子)下标 : i*2+1
???右节点(孩子)下标 : i*2+2
总结
大顶堆:直到最顶端的数是最大值为止。(父节点比左节点、右节点都大)
小顶堆:直到最顶端的数是最小值为止。(父节点比左节点、右节点都小)
维护堆的性质 → 如果不满足条件,就可以在父、左、右节点之间进行交换。
以大顶堆为例,将最大的数与父节点交换。(结合图文解析)
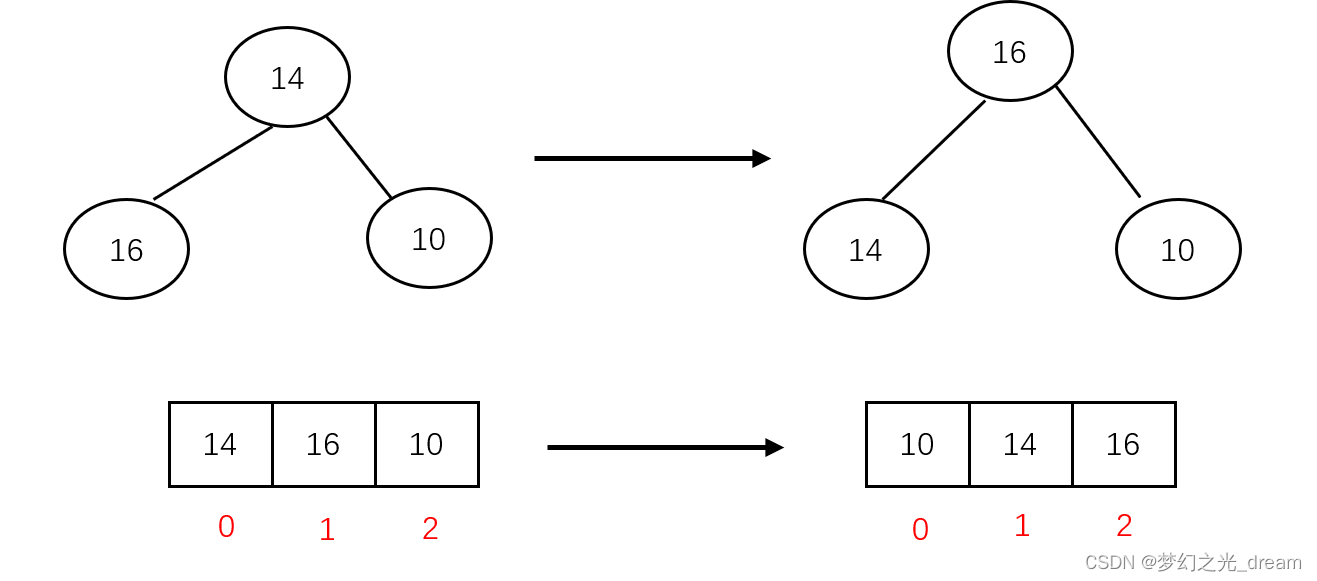
维护时,数组的存储会发生改变。
二.代码 + 运行效果
堆排序的升序代码
/*
1.堆排序:近似完全二叉树的数据结构。
二叉树:结合树的生长,会不断地进行一分为二。
2.维护堆的性质:当出现无序堆的时候,可以及时维护,逐渐地变成有序堆。
arr:存储堆的数组 n:数组长度 i:待维护节点的下标
3.算法的执行步骤:
①建立堆。(按层次遍历,构建一棵完全二叉树)
②节点交换。(从下至上进行调整)
③排序:
(1)交换堆顶节点和末尾节点,得到最大元素 。
(2)调整剩下的节点。
(3)不断地执行(1)(2),直到整个数列有序。
4.总结:大顶堆(直到最顶端的数是最大值为止)。
*/
#include<iostream>
using namespace std;
//第三部分:维护堆的性质
void heap(int arr[],int n,int i){
//假设父节点是最大值
int max=i;
//找到左节点的下标(左孩子)
int leftSon=i*2+1;
//找到右节点的下标 (右孩子)
int rightSon=i*2+2;
//找到左右节点最大的下标
if(leftSon<n && arr[max]<arr[leftSon]){ // 第二个小于改大于会变成降序
max=leftSon;
}
if(rightSon<n && arr[max]<arr[rightSon]){ //第二个小于改大于会变成降序
max=rightSon;
}
//如果有个孩子比父节点大
if(max!=i){
//交换节点
swap(arr[max],arr[i]);
//为何用递归?因为剩余的部分也要交换。
heap(arr,n,max);
}
}
//第二部分:堆排序入口
void heapSort(int arr[],int n){
//建立堆
for(int i=n/2-1;i>=0;i--){ // n/2-1是父节点下标,类似于(i-1)/2
heap(arr,n,i);
}
//排序
for(int i=n-1;i>0;i--){
swap(arr[i],arr[0]);
heap(arr,i,0);
}
}
//第一部分
int main(){
int n;
cin>>n;
int arr[n];
for(int i=0;i<n;i++){
cin>>arr[i];
}
//堆排序
heapSort(arr,n);
for(int i=0;i<n;i++){
cout<<arr[i]<<" ";
}
return 0;
}
输入样例
8
56 66 1 9 37 99 15 101
输出样例
1 9 15 37 56 66 99 101
三.图文解析
堆排序的执行流程
第一步:建立堆。(完全二叉树)
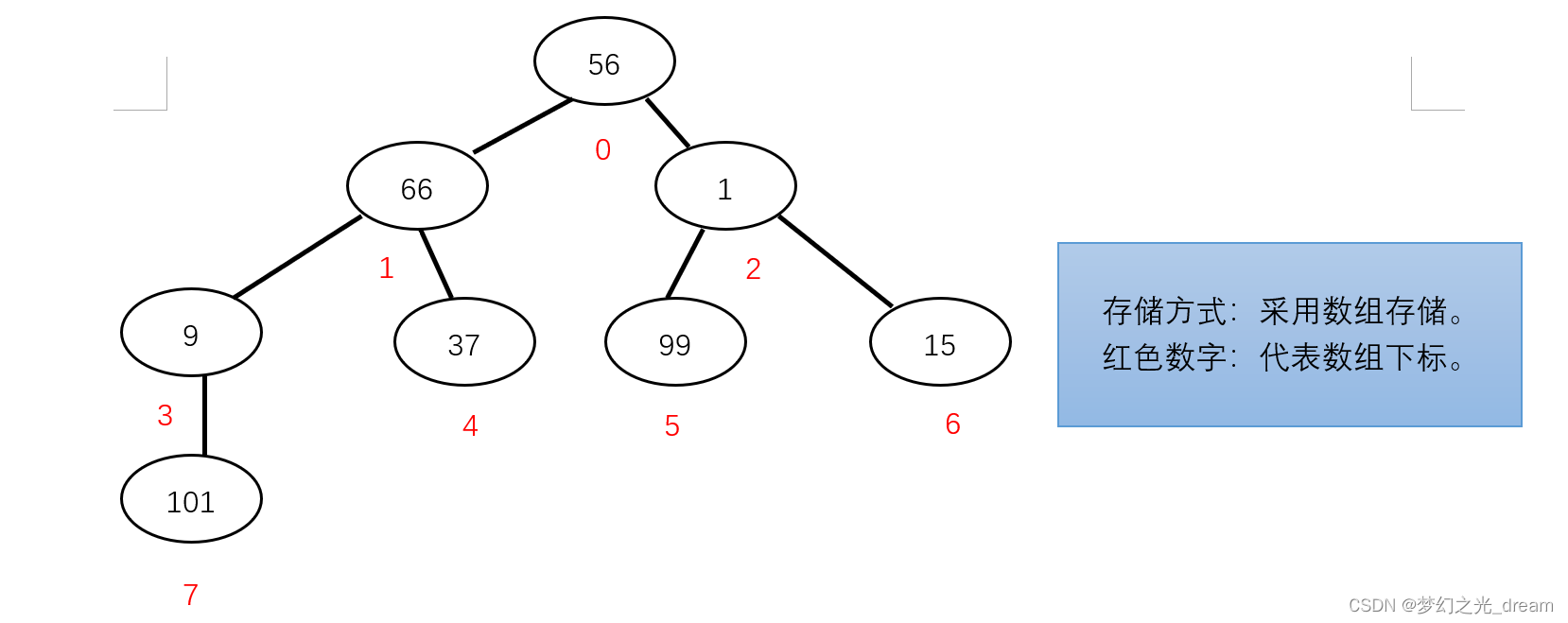
第二步:交换。
66与56交换
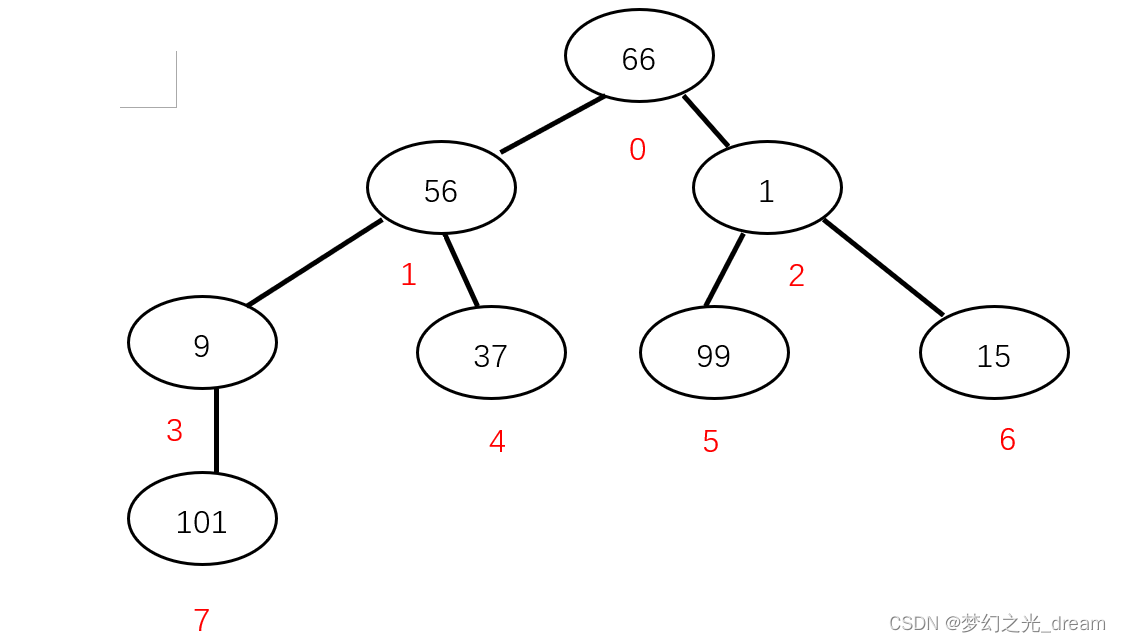
1与99交换

9与101交换
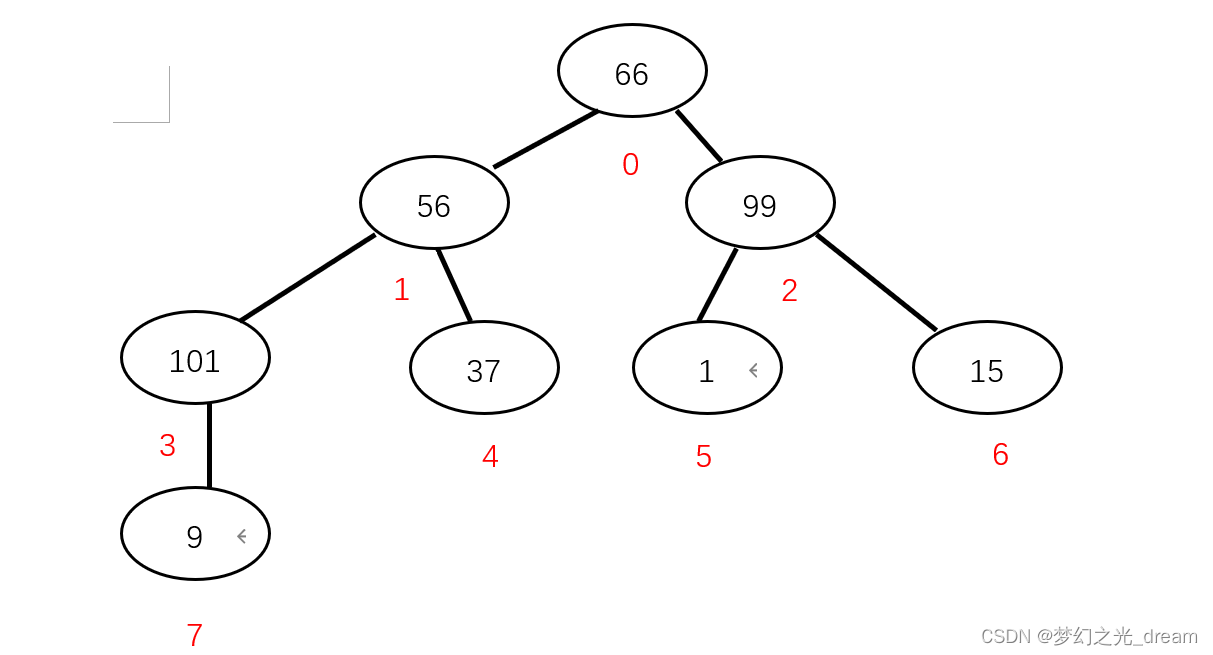
56与101交换
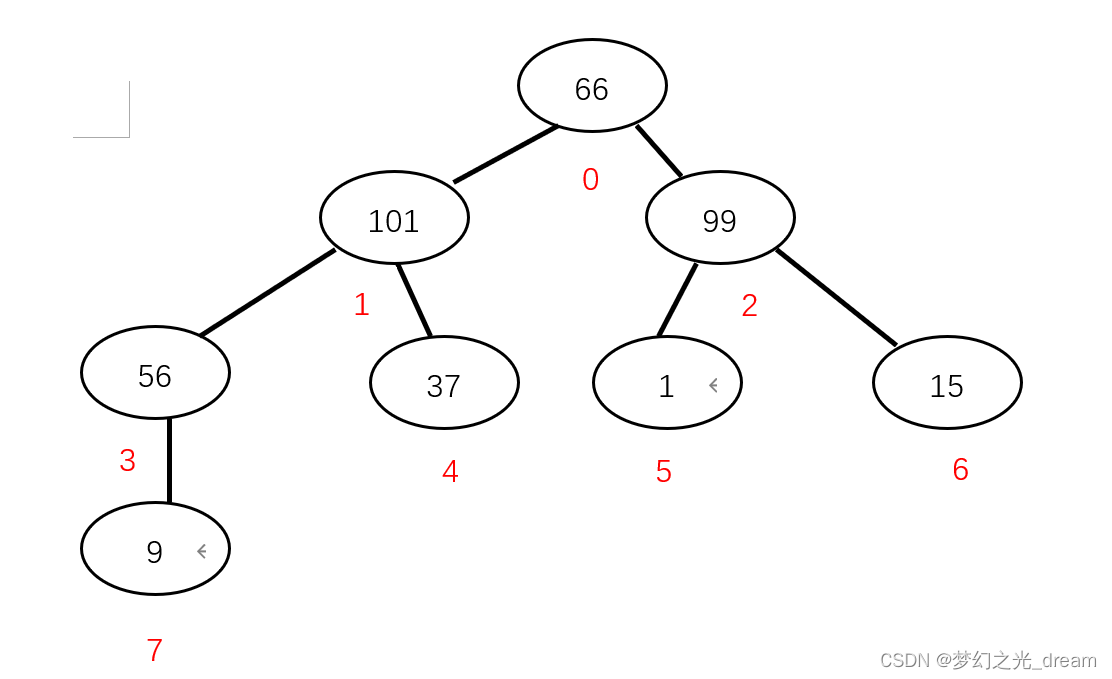
66与101交换
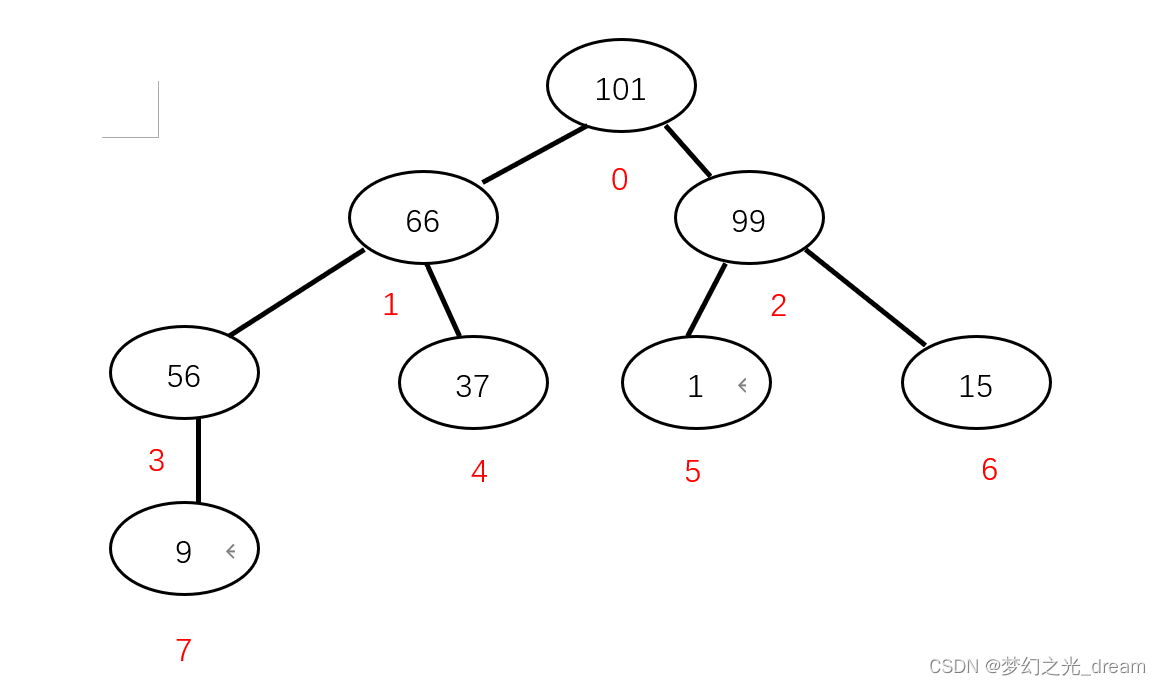
第三步:堆排序。
1.堆顶节点与末尾节点进行交换,得到最大值101。
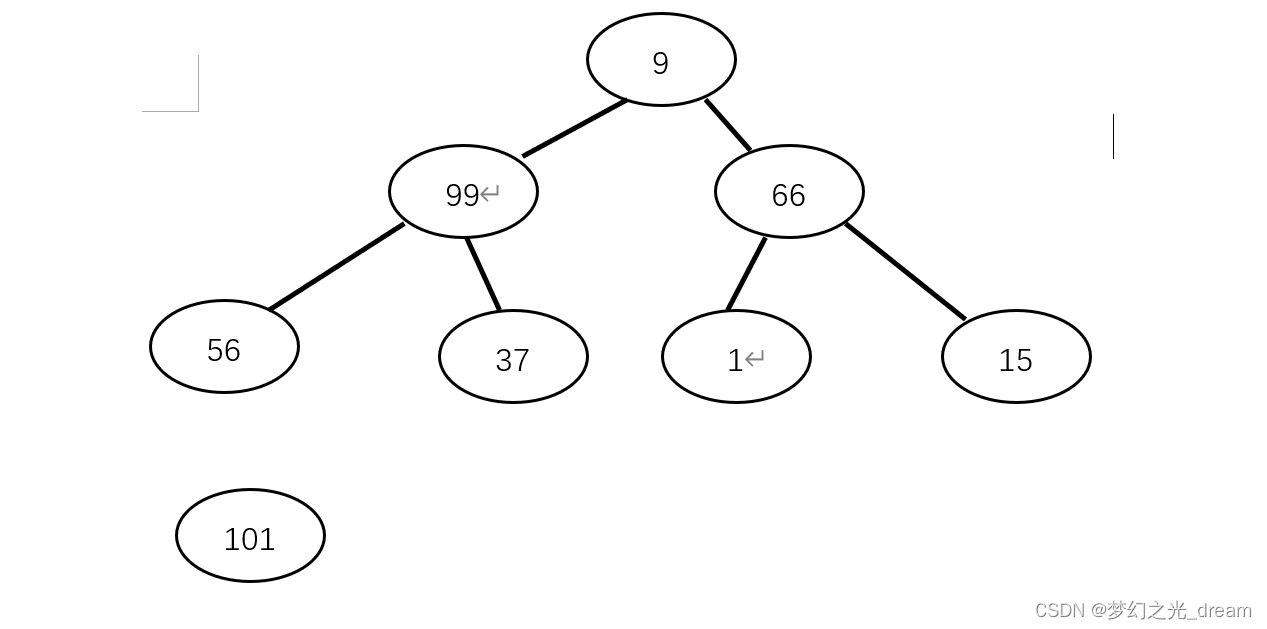
2.重新调整为堆。
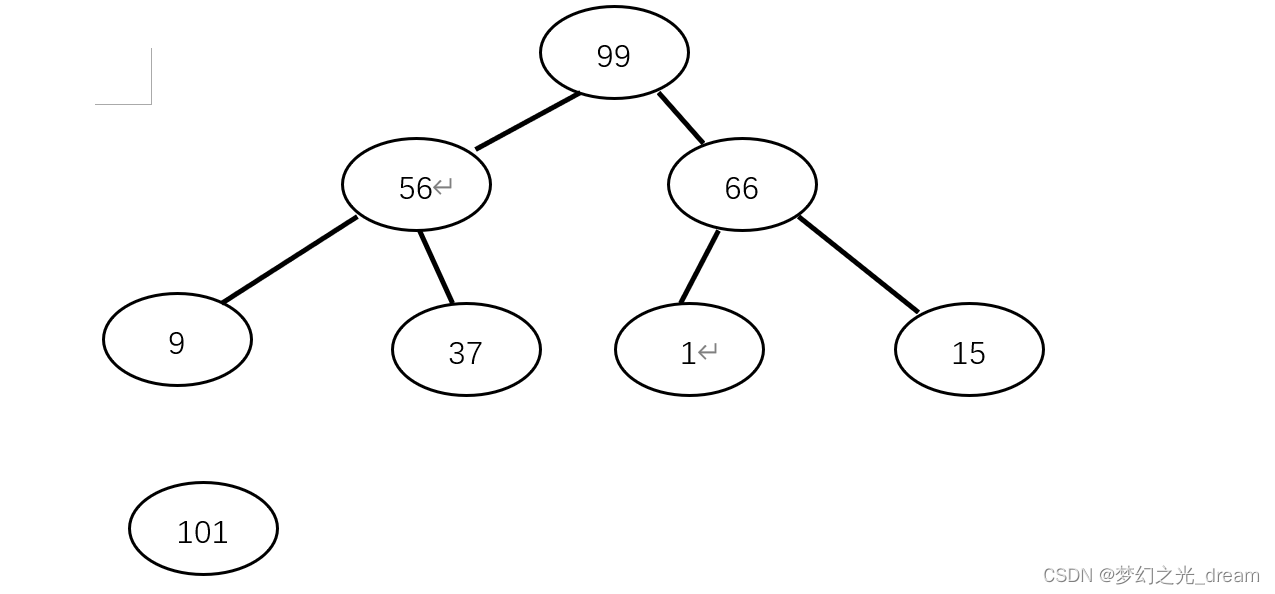
3.依次类推:99与15进行交换,得到最大值99
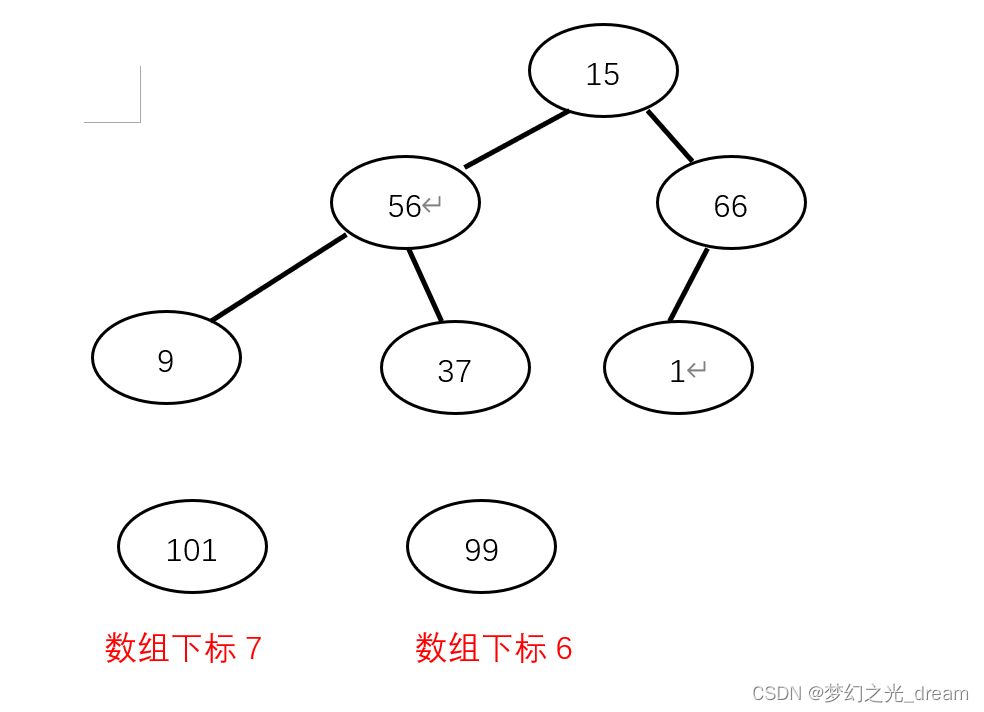
4.依次类推:再次调整为堆。
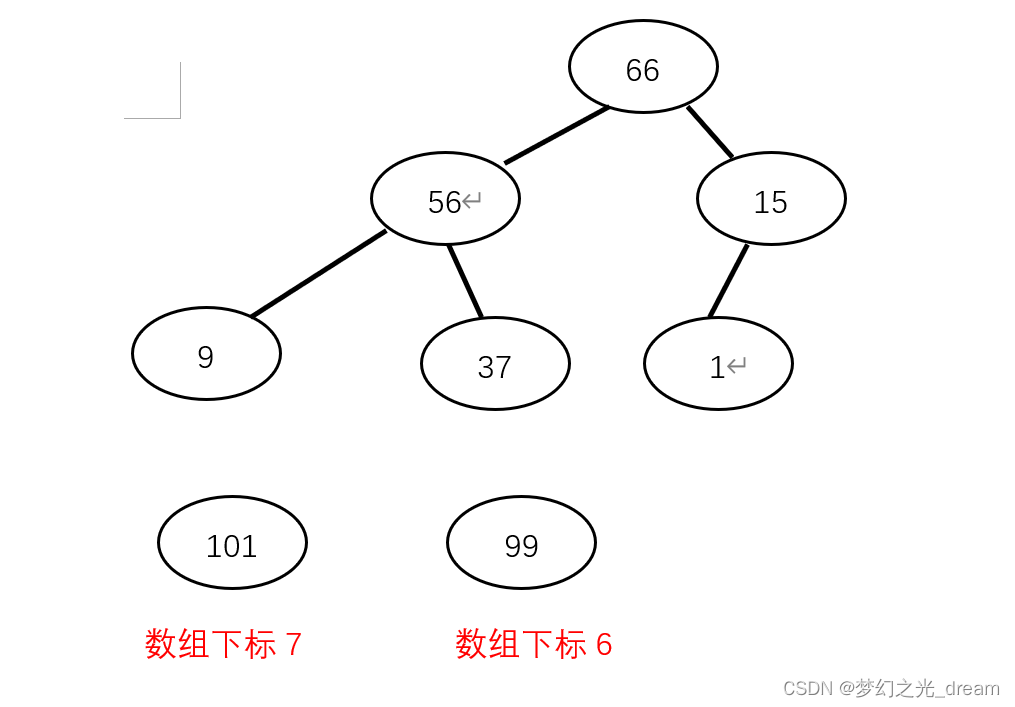
5.依次类推…,直到排序完成。
101 99 66 56 37 15 9 1
根据数组下标的顺序,得出排序结果:
1 9 15 37 56 66 99 101
