[数据结构与算法]动态规划之01背包问题，c++实现

问题描述

01背包问题
问题分析

1. 动态规划法分析：1.划分子问题，2.得出子问题的递推公式，3.填表
2. 划分子问题
   1. 用数组V[n][n]存储价值和重量关系，行表示物体，列表示重量
   2. 第0行和第0列设置为0，没有物体的时候价值没0，重量为0的时候物体无论多少价值也为0
   3. 如果第i个物体重量小于当前总重量j，则取前i-1和第i个物体组合的最优值，否则该物体不可以放进背包，取前i-1个物体的最优价值
3. 递推公式
   1. 不装入背包时：V(i-1, j) j < wi
   2. 装入背包时：max{V(i-1, j), V(i-1, j-wi)+vi } j >= wi
   3. V(i-1, j-wi)+vi 表示用当前值和子问题的解结合，取最优
4. 填表
   

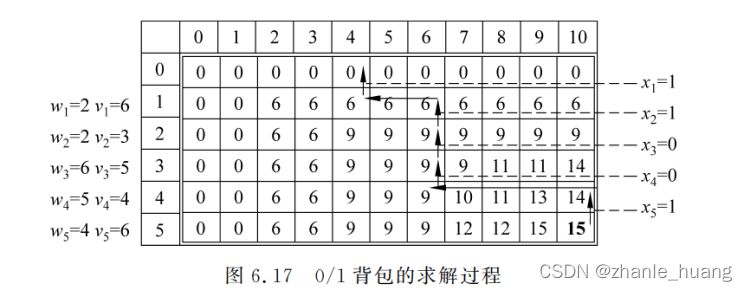
算法实现

#include<iostream>
using namespace std;
struct Node {
	int value;
	int weight;
}; 

// 物体，长度 
void packageHander(Node arr[], int n, int c) {
	int V[n][c+1], i;
	// 第0行和第0列设置为0，没有物体的时候价值没0，重量3为0的时候物体无论多少价值也为0
	for (i = 0; i < n; i++) {
		V[i][0] = 0;
	} 
	for (i = 0; i <= c; i++) {
		V[0][i] = 0;
	} 
	for (i = 1; i < n; i++) {
		// 重量从1到c 
		for (int j = 1; j <= c; j++) {
			// 重量小于目前总量 
			// 如果第i个物体重量小于当前总重量j，则取前i-1和第i个物体组合的最优值，否则该物体不可以放进背包，取前i-1个物体的最优价值 
			if (arr[i-1].weight <= j) {
				V[i][j] = max(V[i-1][j], V[i-1][j-arr[i-1].weight]+arr[i-1].value);
			} else {
				V[i][j] = V[i-1][j];
			}
		} 
	}
	for (i = 0; i <= c; i++) {
		cout<<i<<"\t";
	}
	cout<<endl;
	for (i = 0; i < n; i++) {
		for (int j = 0; j <= c; j++) {
			cout<<V[i][j]<<"\t";
		}
		cout<<endl;
	}
	int j = 0;
	// 如果当前值比前一个值大，说明被取了，就取当前值，然后减去重量，重量作为列 
	for ( i=n, j=c; i>0; i--) {
		if (V[i][j] > V[i-1][j]) {
			x[i-1] = 1;
			j = j - arr[i-1].weight;
		} else {
			x[i-1] = 0;
		} 
	}
	cout<<"选取方案为"; 
	for (i = 0; i<n-1; i++) {
		cout<<x[i]<<" ";
	}
	cout<<endl;
}


int main() {
	int n = 6;
	Node a[n];
	a[0].value = 6;
	a[0].weight = 2;
	a[1].value = 3;
	a[1].weight = 2;
	a[2].value = 5;
	a[2].weight = 6;
	a[3].value = 4;
	a[3].weight = 5;
	a[4].value = 6;
	a[4].weight = 4;
	for (int i = 0; i < n-1; i++) {
		cout<<"val"<<a[i].value<<"weight"<<a[i].weight<<endl;
	}
	packageHander(a, n, 10);
	return 0;
} 

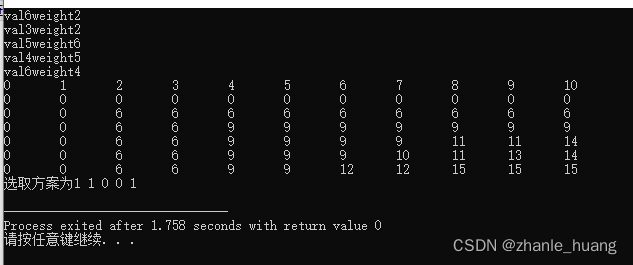
结果

《新程序员》：云原生和全面数字化实践

50位技术专家共同创作，文字、视频、音频交互阅读