图的DFS与BFS和二叉树原理是一样的,不过在保存遍历序列的时候要注意,一般C#中用List来保存序列,而List是引用类型。
DFS主要是利用递归的方式,不同问题中递归的结束的条件可能有所不同。
BFS采用队列的方式,不过队列的类型不一定是节点,也可能是List,即序列,比如需要求某两点之间的路径的时候。
所有可能的路径
给你一个有 n 个节点的 有向无环图(DAG),请你找出所有从节点 0 到节点 n-1 的路径并输出(不要求按特定顺序) 。graph[i] 是一个从节点 i 可以访问的所有节点的列表(即从节点 i 到节点 graph[i][j]存在一条有向边)。
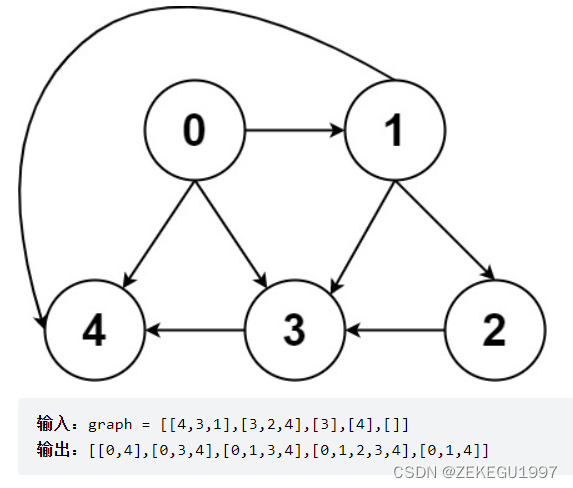
?下面用两种方法分别解题。
DFS
这里的难点有两个:一是注意要用一个list来记录遍历的序列,然后保存时要创建一个新的list,否则记录后面的序列会改变之前保存的序列。
二是在遍历到目标节点和每个节点的最后一一个节点时要回退,即删除序列中的最后一个数,这个通过手动走一遍遍历过程就会理解。
public class Solution {
public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {
IList<IList<int>> res=new List<IList<int>>();
List<int> temp=new List<int>();
DFS(graph,0,temp,res);
return res;
}
public void DFS(int[][] graph,int i,List<int> temp,IList<IList<int>> res)
{
temp.Add(i);
if(i==graph.Length-1)
{
List<int> save=new List<int>();
save.AddRange(temp);
res.Add(save);
temp.RemoveAt(temp.Count-1);
}
else
{
for(int j=0;j<graph[i].Length;j++)
{
DFS(graph,graph[i][j],temp,res);
}
temp.RemoveAt(temp.Count-1);
}
}
}BFS
这里要注意的第一点和上面一样,第二是队列中要保存的是目前为止的序列。
public class Solution {
public IList<IList<int>> AllPathsSourceTarget(int[][] graph) {
Queue<List<int>> q=new Queue<List<int>>();
IList<IList<int>> res=new List<IList<int>>();
List<int> temp=new List<int>();
temp.Add(0);
q.Enqueue(temp);
while(q.Count!=0)
{
List<int> de=new List<int>();
de=q.Dequeue();
if(de[de.Count-1]==graph.Length-1)
res.Add(de);
else
for(int i=0;i<graph[de[de.Count-1]].Length;i++)
{
List<int> t=new List<int>();
t.AddRange(de);t.Add(graph[de[de.Count-1]][i]);
q.Enqueue(t);
}
}
return res;
}
}