[数据结构与算法]「洛谷」P1196 银河英雄传说

P1196 银河英雄传说

https://www.luogu.com.cn/problem/P1196

题目描述

杨威利擅长排兵布阵，巧妙运用各种战术屡次以少胜多，难免恣生骄气。在这次决战中，他将巴米利恩星域战场划分成 30000 列，每列依次编号为 $1,2,\dots ,30000$。之后，他把自己的战舰也依次编号为 $1,2,\dots ,30000$，让第 i 号战舰处于第 i 列，形成“一字长蛇阵”，诱敌深入。这是初始阵形。当进犯之敌到达时，杨威利会多次发布合并指令，将大部分战舰集中在某几列上，实施密集攻击。合并指令为 M i j，含义为第 i 号战舰所在的整个战舰队列，作为一个整体（头在前尾在后）接至第 j 号战舰所在的战舰队列的尾部。显然战舰队列是由处于同一列的一个或多个战舰组成的。合并指令的执行结果会使队列增大。

然而，老谋深算的莱因哈特早已在战略上取得了主动。在交战中，他可以通过庞大的情报网络随时监听杨威利的舰队调动指令。

在杨威利发布指令调动舰队的同时，莱因哈特为了及时了解当前杨威利的战舰分布情况，也会发出一些询问指令：C i j。该指令意思是，询问电脑，杨威利的第 i 号战舰与第 j号战舰当前是否在同一列中，如果在同一列中，那么它们之间布置有多少战舰。

作为一个资深的高级程序设计员，你被要求编写程序分析杨威利的指令，以及回答莱因哈特的询问。

输入描述

第一行有一个整数 T（$1\le T\le 5\times 10^5$），表示总共有 T 条指令。
以下有 T 行，每行有一条指令。指令有两种格式：

1. M i j：i 和 j 是两个整数（$1\le i,j\le 30000$），表示指令涉及的战舰编号。该指令是莱因哈特窃听到的杨威利发布的舰队调动指令，并且保证第 i 号战舰与第 j 号战舰不在同一列。
2. C i j：i 和 j 是两个整数（$1\le i,j\le 30000$），表示指令涉及的战舰编号。该指令是莱因哈特发布的询问指令。

输出描述

依次对输入的每一条指令进行分析和处理：
如果是杨威利发布的舰队调动指令，则表示舰队排列发生了变化，你的程序要注意到这一点，但是不要输出任何信息。
如果是莱因哈特发布的询问指令，你的程序要输出一行，仅包含一个整数，表示在同一列上，第 i 号战舰与第 j 号战舰之间布置的战舰数目。如果第 i 号战舰与第 j 号战舰当前不在同一列上，则输出 -1。

样例

#1

4
M 2 3
C 1 2
M 2 4
C 4 2

-1
1

提示

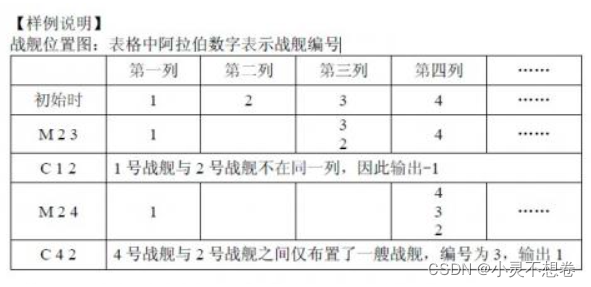
解析

不得不说，这题我在 AcWing 过了，但在洛谷没过，一直 WA 爆零（同一份代码），经过数个小时的努力，我发现洛谷用 br.read() 居然会读入错误，就是不报错，只是读入的东西奇奇怪怪的，不是我想要的。😠 🔥

废话不多话，开始正文 😁

很明显的，我们知道这题要用并查集，先明确题目要求的东西：

• 要维护船之间的关系（某船与某船是否属于同一列）
• 同一列船之间某两个船之间有多少条船

首先第一个问题，很明显我们应该要用并查集。

但对于第二个问题，如何在并查集的基础之上去实现呢？

要求 $x$ 与 $y$ 之间有多少船，看看数据量 30000 多，500000 次询问，如果每次都一个一个的找，那么必然 TLE，文尾放有这种思路 44 分代码。

正确思路： 使用前缀和的思路，以列为一个单元，求这一列到队头（船头）距离，如下图所示：

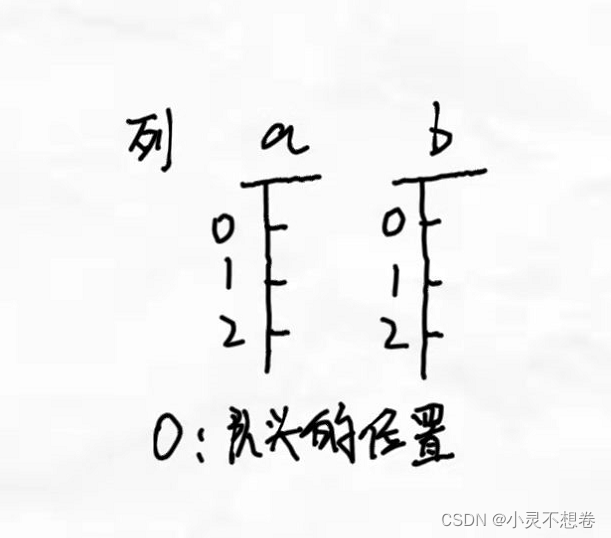
使用 $dis[x]$ 数组来表示船 x 到队头的距离，初始时 $dis[x]=0$ ，在进行合并操作时，只需要更新当前队头 $x$ 就行，因为利用路径压缩的特性我们可以更新其它的孩子，最后求差就是 abs(dis[x] - dis[y]) - 1 就好啦。

利用 $size[x]$ 数组来表示当前 x 队列有多少支船。

AC Code

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(br);
    static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));

    static final int MAX = 30005;
    static int[] fa = new int[MAX];   // 船之间关系
    static int[] dis = new int[MAX];  // 船 x 到该队列船头的距离
    static int[] size = new int[MAX]; // 该队列一共有多少船

    public static void main(String[] args) throws Exception {
        int T = nextInt();
        for(int i = 1; i < MAX; i++) {
            fa[i] = i;
            size[i] = 1;
        }
        while(T-- != 0) {
            int opt = br.read();
            int x = nextInt(), y = nextInt();
            find(2); // 避免树的深度太深（StackOverflow），因此每次都走一遍 find() 【学习某位大佬的】
            if(opt == 'M') {
                union(x, y);
            } else if(opt == 'C') {
                int a = find(x);
                int b = find(y);
                if(a == b) {
                    int res = Math.abs(dis[x] - dis[y]) - 1;
                    out.println(Math.max(res, 0));
                } else {
                    out.println(-1);
                }
            }
        }
        out.flush();
    }

    public static int find(int x) {
        if(fa[x] == x) return x;
        int root = find(fa[x]);
        dis[x] += dis[fa[x]]; // 更新 x 船到祖先队列船头的距离
        return fa[x] = root;
    }

    public static void union(int x, int y) {
        x = find(x);
        y = find(y);
        fa[x] = y; // 将 x 接到 y 的末尾
        dis[x] = size[y]; // x 队列的船头距离 y 队列的船头
        size[y] += size[x]; // 队列 y 新增 x 队列的所有船
        size[x] = 0; // x 队列没船了
    }

    public static int nextInt() throws Exception {
        st.nextToken();
        return (int) st.nval;
    }
    
    public static String nextStr() throws Exception {
        st.nextToken();
        return st.sval;
    }
}

44 分 —— 终究还是太菜

import java.io.*;
import java.math.*;
import java.util.*;

public class Main {
    static BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
    static StreamTokenizer st = new StreamTokenizer(br);
    static PrintWriter out = new PrintWriter(new BufferedOutputStream(System.out));

    static final int MAX = 30005;
    static ArrayList<Integer>[] list = new ArrayList[MAX];
    static int[] fa = new int[MAX];

    public static void main(String[] args) throws Exception {
        int T = nextInt();
        for(int i = 1; i < MAX; i++) {
            list[i] = new ArrayList<>();
            list[i].add(i);
            fa[i] = i;
        }
        while(T-- != 0) {
            char opt = nextStr().charAt(0);
            int x = nextInt(), y = nextInt();
            if(opt == 'M') {
                union(x, y);
            } else if(opt == 'C') {
                int a = find(x);
                int b = find(y);
                if(a == b) {
                    int ta = list[a].indexOf(x);
                    int tb = list[a].indexOf(y);
                    ta = Math.abs(ta);
                    tb = Math.abs(tb);
                    int sum = Math.abs(tb - ta);
                    out.println(Math.abs(sum - 1));
                    continue;
                }
                out.println(-1);
            }
        }
        out.flush();
    }

    public static int find(int x) {
        return fa[x] == x ? x : (fa[x] = find(fa[x]));
    }

    public static void union(int x, int y) {
        x = find(x);
        y = find(y);
        if(x == y) return;
        while(!list[x].isEmpty()) {
            list[y].add(list[x].remove(0));
        }
        fa[x] = y;
    }

    public static int nextInt() throws Exception {
        st.nextToken();
        return (int) st.nval;
    }
    public static String nextStr() throws Exception {
        st.nextToken();
        return st.sval;
    }
}

《新程序员》：云原生和全面数字化实践

50位技术专家共同创作，文字、视频、音频交互阅读