[数据结构与算法]python 实现 熵值法 确定指标权重

步骤：

设指标共p个，评价对象共g个，则构成评价值（得分）矩阵如下：

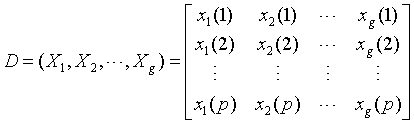
xj(i)表示评价对象j在指标i上的评价值，j=1,2,...,g i=1,2,...,p

指标i对应的熵值为ei的计算公式如下：

根据熵值来计算指标i的权重wi，计算公式如下:

?

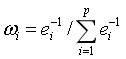?程序：

（4个指标，3个评价对象）

import math

class entropyMethod:
    def __init__(self, array):
        self.array = array

    def getEntropy(self):
        entropy_list = []
        for j in range(len(self.array[0])):
            list1 = []
            for i in range(len(self.array)):
                x1 = self.array[i][j] * math.log(self.array[i][j])
                list1.append(x1)
            entropy = (-sum(list1)) / math.log(len(self.array))
            entropy_list.append(entropy)
        return entropy_list

    def getWeight(self):
        weight_list = []
        entropy_list = self.getEntropy()
        entropyReciprocal_list = []
        for entropy in entropy_list:
            entropyReciprocal_list.append(1/entropy)
        for entropy in entropy_list:
            weight = (1 / entropy) / sum(entropyReciprocal_list)
            weight_list.append(weight)
        return weight_list
if __name__ == '__main__':
    matrix = [
        [90,95,94,85],
        [86,58,72,91],
        [88,15,95,92],
    ]
    entropy_list = entropyMethod(matrix).getEntropy()
    weight_list = entropyMethod(matrix).getWeight()
    for weight_list in weight_list:
        print(weight_list)

结果：

????????结果和熵值法基本思想一致，即离散程度越大的指标，其权重应越大。程序的举的例子中矩阵第2列（即第2个指标的离散程度最大），可以发现该指标的权重结果也越大，结果约0.358?

《新程序员》：云原生和全面数字化实践

50位技术专家共同创作，文字、视频、音频交互阅读