开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 数据结构与算法 -> 计算机算法设计与分析之----- 递归与分治策略 -> 正文阅读

[数据结构与算法]计算机算法设计与分析之----- 递归与分治策略

【Master定理】

主定理【Master定理】提供了分治方法带来的递归表达式的渐进复杂度分析。
将规模为 n 的问题通过分治，得到 a 个规模为 n/b 的问题，每次递归带来的额外计算为 $c(n^d)$
即 $T (n) = a (n / b) + c (n d)$

若 $a = b d, T (n) = O (n d l o g (n))$
若 $a < b d, T (n) = O (n d)$
若 $a > b d, T (n) = O (n l o g b (a))$

快速排序

快速排序算法是基于分治策略的另一个排序算法。其基本思想是，对于输入的子数组a【p:r】，按以下三个步骤进行排序。
①分解(Divide) :以a【p】为基准元素将a【p : 】划分成3段a 【p : q-1) ,a 【g】和a【g+1 :r】，使ap : q-1】中任何一个元素小于等于a 【g】，而a【q+1:】中任何一个元素大于等于a【g】】。下标q在划分过程中确定。
②递归求解(Conquer):通过递归调用快速排序算法，分别对a 【p : q-1】和a【g+1:】进行排序。
③合并(Merge):由于对a 【p: q-1】和a【g+1 : r】的排序是就地进行的，因此在a【p: g-1】和a 【g+1 :r】都已排好的序后，不需要执行任何计算，a【p: r】则已排好序。
基于这个思想，可实现快速排序算法如下:

根据基本思路，得到以下代码:

对应的题目【模板】快速排序

代码:

#include<iostream>
#include<algorithm>
using namespace std;

const int N = 1E5 + 10;

int n , a[N];

int Partition(int a[] , int p ,int r){
    int i = p , j = r + 1 ;
    int x = a[p];
    while(true){
        while(a[++i] < x && i < r ); // 我们向右拓展，直到找到一个比 x 大或者等于的
        while(a[--j] > x ); // 我们向左延伸，直到遇到一个 <= x 的数
        if(i >= j)break; // 因为有不等式 a[i] >= x >= a[j] ，也就是最终i应该在x 右边，j在其左边
        swap(a[i],a[j]); // 但 j 如果在右边，i在左边，则交换
    }
    a[p] = a[j] , a[j] = x; // j为划分点
    return j;
}

void qsort(int a[] , int p , int r){
    if(p < r){
        int q = Partition(a , p ,r); // 分解，分为以 a[q]为界限分为三段
        qsort(a , p ,q - 1); // 对左半段排序
        qsort(a , q + 1 ,r); // 对右半段排序
    }
}

int main(){
    cin>>n;
    for(int i = 1 ; i <= n ; ++i)cin>>a[i];
    qsort(a , 1 , n);
    for(int i = 1 ; i <= n ; ++i)cout<<a[i]<<" ";
    return 0;
}

快速排序的运行时间与划分是否对称有关，其最坏情况发生在划分过程产生的两个区域分别包含n-1个元素和1个元素的时候。由于函数Partition)的计算时间为O(n)，所以如果算法Partition的每步都出现这种不对称划分，则其计算时间复杂性T(n)满足
$\begin{cases} O(1) & n <= 1 \\ T(n-1) O(n) & x >1 \\ \end{cases}$

我们可以通过递归子树来求解。如下图
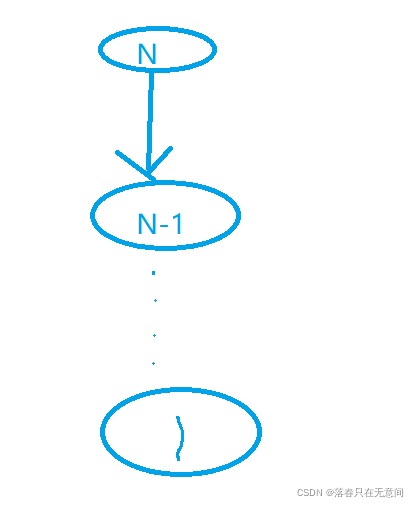
在这里插入图片描述
这很明显是一个等差数列，我们利用求和公式很容易解出，此递归方程，可得 $T(n) = O(n^2)$ 。
在最好情况下，每次划分所取的基准都恰好为中值，即每次划分都产生两个大小为n/2的区域，此时，Partition算法的计算时间T(n)满足
$\begin{cases} O(1) & n <= 1 \\ 2T(n/2) + O(n) & x >1 \\ \end{cases}$
由Master定理其解为T(n)=O(nlogn)。

优化

容易看到，快速排序算法的性能取决于划分的对称性。通过修改函数Partition()，可以设计出采用随机选择策略的快速排序算法。在快速排序算法的每步中，当数组还没有被划分时，可以在alp:r]中随机选出一个元素作为划分基准，这样可以使划分基准的选择是随机的,从而可以期望划分是较对称的。随机化的划分算法可实现如下:

// 在[p,r]中随机选一个作为划分点，而不总是以最左边的作为
int Randomize(int a[] ,int p ,int r){
    srand((unsigned)time(NULL));     //这里利用时间进行播种，需要time.h
    int i = rand()%(r - p + 1) + p;
    swap(a[i],a[p]);
    return Partition(a,p,r);
}

代码:

#include<iostream>
#include<algorithm>
#include<cstdlib>
#include<time.h>
using namespace std;

const int N = 1E5 + 10;

int n , a[N];

int Partition(int a[] , int p ,int r){
    int i = p , j = r + 1 ;
    int x = a[p];
    while(true){
        while(a[++i] < x && i < r );
        while(a[--j] > x );
        if(i >= j)break;
        swap(a[i],a[j]);
    }
    a[p] = a[j] , a[j] = x;
    return j;
}
// 在[p,r]中随机选一个作为划分点，而不总是以最左边的作为
int Randomize(int a[] ,int p ,int r){
    srand((unsigned)time(NULL));     //这里利用时间进行播种，需要time.h
    int i = rand()%(r - p + 1) + p;
    swap(a[i],a[p]);
    return Partition(a,p,r);
}



void qsort(int a[] , int p , int r){
    if(p < r){
        int q = Randomize(a , p ,r);
        qsort(a , p ,q - 1);
        qsort(a , q + 1 ,r);
    }
}

int main(){
    cin>>n;
    for(int i = 1 ; i <= n ; ++i)scanf("%d",&a[i]);
    qsort(a , 1 , n);
    for(int i = 1 ; i <= n ; ++i)cout<<a[i]<<" ";
    return 0;
}

结果
快了很多，上面代码还需要吸氧才能过
在这里插入图片描述

逆序对(归并算法)

合并排序算法是用分治策略实现对n个元素进行排序的算法，其基本思想是:将待排序元素分成大小大致相同的两个子集合，分别对两个子集合进行排序，最终将排好序的子集合合并成要求的排好序的集合。
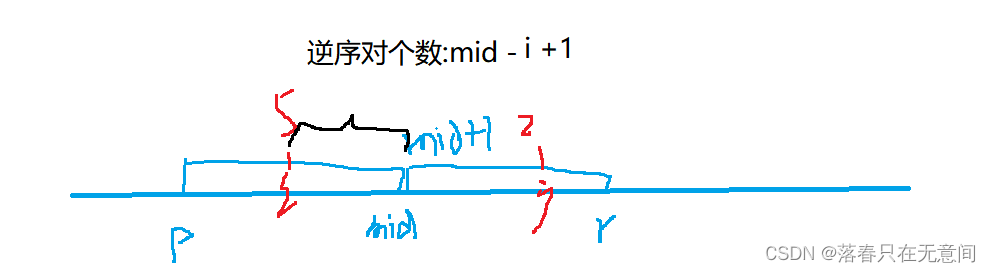
由于我们在和并的时候，左右两边的集合都是排好序的，那么如果后一个集合中有一个元素小于前一个集合，那么就存在从前一个集合到其末尾的元素个数的逆序对个数，因此在当前元素后边的值都大于等于该元素，那么当前元素比后面集合中的元素大，那么其后边的元素也一定会比它大。

在这里插入图片描述
相关题目：逆序对

代码:

#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
const int N = 5e5 + 10;

int n ,a[N],c[N];
long long cnt;


void mgsort(int a[],int p ,int r){
    if(p >= r)return ;
    int mid = (p + r)>>1;
    mgsort(a , p , mid);
    mgsort(a , mid + 1 ,r);
    int  k = p , i = p , j = mid + 1;
    while(i <= mid && j <= r){
        if(a[i] <= a[j]) c[k++] = a[i++];
        else c[k++] = a[j++]  , cnt += mid - i + 1;
    }
    while(i <= mid)c[k++] = a[i++];
    while(j <= r)c[k++] = a[j++] , cnt += mid - i + 1;
    for( i = p ; i <= r ; ++i)a[i] = c[i];
}

int main(){
    scanf("%d",&n);
    for(int i = 1 ; i <= n ; ++i)scanf("%d",&a[i]);
    mgsort(a,1,n);
    cout<<cnt<<endl;
    return 0;
}

火柴排队[NOIP2013 提高组]

题目链接: 火柴排队

解题思路:
首先要想按什么排法，才能使得距离(题目定义的)的最小呢？当时我想到的是用贪心来证明两个序列相对位置相同的在一行能使得距离最小。贪心证明如下
在这里插入图片描述
可能证明得不是很严谨，这里附上较严谨的证明

题目的意思：min{∑（ai-bi）^2 (1<=i<=n)}
展开：min{∑（ai^2+bi2-2aibi）}=min{∑ai^2+∑bi2-∑2aibi}
仔细观察，可以发现∑ai^2和∑bi2的值是不会变的，所以只能在∑2aibi上做文章。
为使得和最小，那么∑2aibi要最大，本题的模型就转变为max{∑ai*bi}。

转化为证明：顺序之乘>=乱序之乘

设有序数列k1_kn,p1pn，取k1<k2、p1<p2
因此容易得到：k1p1+k2p2>k1p2+k2p1;
将上述不等式变形一下：
k2p2-k2p1>k1p2-k1p1 即k2(p2-p1)>k1(p2-p1)
∵k2>k1,p2>p1 ∴k2(p2-p1)>k1(p2-p1)
证毕；
推广2中的结论到1中，乱序就是不断将顺序交换打乱的过程，最终结果符合2的结论，因此顺序之乘>=乱序之乘，证毕。

实现方法

首先，我们先求出去，序列中数字应该所在的位置，而现在所处在的位置的序列，这里应该在的位置我们可以用一个数组的下标表示，当前所处的置，我们可以让这个数组刚开始的值是每一个值所在的标号，然后排序，排序代码如下，

bool cmp1(int x , int y){ return a[x] < a[y];}

之后，我们令 q[a[i]] = b[i]，相当于以 a[i]为关键字对序列 b[i] 排序。
若序列 a 与序列 b 相等，那么此时 q[a[i]]应该等于 a[i] 的，也就是 q[i] = i。
那么也就是说如果我们想让序列 a 与序列 b 相等，那么我们需要让 q 升序排列。
问题就变为，将原本乱的 q 序列升序排列的最少交换次数。那么我们需要对这个数组求逆序对即可。

代码:

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1e5 + 10 , mod = 99999997; 

int n ;
int a[N],b[N],c[N],d[N];
int q[N],cnt , t[N];

bool cmp1(int x , int y){ return a[x] < a[y];}
bool cmp2(int x, int y){ return b[x] < b[y] ; }

void mgsort(int a[] , int p , int r){
    if(p >= r)return ;
    int mid = (p + r) >>1;
    mgsort(a , p , mid) , mgsort(a , mid + 1 ,r);
    int i = p , k = p , j = mid + 1;
    while(i <= mid && j <= r){
        if(a[i] <= a[j])t[k++] = a[i++];
        else t[k++] = a[j++] , cnt =( cnt +  mid - i + 1) % mod;
    }
    while(i <= mid) t[k++] = a[i++];
    while(j <= r) t[k++] = a[j++] , cnt =( cnt +  mid - i + 1) % mod;
    for(i = p ; i <= r ; ++i)a[i] = t[i];
}

int main(){
    cin>>n;
    for(int i = 1 ; i <= n ; ++i)scanf("%d",&a[i]) , c[i] = i;
    for(int j = 1 ; j <= n ; ++j)scanf("%d",&b[j]) , d[j] = j;
    sort(c + 1 , c + 1 + n , cmp1) ,sort(d + 1 , d + 1 + n , cmp2);
    for(int i = 1; i <= n ; ++i)q[c[i]] = d[i];
    mgsort(q , 1 , n);
    cout<<cnt % mod<<endl;
    return 0;
}

集合求和

题目链接:集合求和

方法一: 递归 (2^n )

对于一个数我们有选和不选两种情况，因此我们在dfs的时候分两种情况。不过这个题目的n = 30 ，很明显会超时。

代码:

#include<iostream>
#include<cmath>
using namespace std;

typedef long long LL;
const int N = 31;
LL sum ;
int a[N] , n;

void dfs(LL s , int u){
    if(u == n){
        sum += s;
        return ;
    }
    dfs(s + a[u] , u + 1);
    dfs(s , u + 1);
}

int main(){
    while(cin>>a[n++]);
    n--;
    dfs(0,0);
    cout<<sum<<endl;
    return 0;
}

方法二: 组合数学知识

由于是求出子集的和，我们不一定要枚举所有子集的情况。我们只需要知道，一个数出现在子集中的次数即可。那么对于集合中的一个数，它出现在不同子集中的次数是多少次呢？那么如果我们选了当前数，那么能出现这个数的子集个数，是由剩余的n-1个数来决定的，那么对于其余的n-1的数，每一个都有选与不选两种可能，所以一共有 $2^{n-1}$ 中。也就是一个数会出现 $2^{n-1}$ 。因此子集和就是：
$\sum_{i=1}^n2^{n-1} * a[i]$

代码:

#include<iostream>
#include<cmath>
using namespace std;

typedef long long LL;
const int N = 31;
LL sum ;
int a[N] , n;

void dfs(LL s , int u){
    if(u == n){
        sum += s;
        return ;
    }
    dfs(s + a[u] , u + 1);
    dfs(s , u + 1);
}

int main(){
    while(cin>>a[n++]);
    n--;
    for(int i = 0 ; i < n ; ++i) sum += a[i] * (LL)pow(2,n-1);
    cout<<sum<<endl;
    return 0;
}

[HNOI2008]越狱(快速幂分治)

题目链接:越狱

解题思路
这其实思路来自于组合数学，我们正难则反，我们知道，m个信仰，n个房间，那么总的方案数有 $m^n$ 中，那么不会出现越狱的情况是有多少种呢？对于第一个监狱我们有m中选择，那么第二个为了不冲突只有m-1中选择，那么第三个呢？m-2？不是的也是m-1种，因为第一个房间的选择它也可以选择，只是不能选与第二个房间相同的，类比，我们发现，从第二个房间开始后边的房间都有 m - 1 种选择，那么我们答案就是
$ans=m ^n ?m?(m?1) ^{n?1}$ ，其中m 可以提出来，就是 $ans=m * （m ^n ?(m?1) ^{n?1}）$

这里可能属于分治类的可能是我们求解这个答案的时候用到了快速幂吧，

ps ：注意输入会爆int ，同时相减的时候可能会变成负数，因此我们相减的时候再 + mod 再取模
代码

#include<iostream>
using namespace std;
const int mod = 100003;
typedef long long LL;

LL n , m, ans ;

LL qmi(LL a , LL b){
    LL ans = 1;
    for( ; b ; b >>= 1){
        if(b & 1)ans = (ans * a) % mod;
        a = a * a % mod;
    }
    return ans % mod;
}

int main(){
    cin>>m>>n;
    LL a = qmi(m  , n - 1) ;
    LL b = qmi(m - 1 , n - 1);
    ans = (a - b + mod) % mod;
    cout<<(ans * m) % mod <<endl;
    return 0;
}

平面上的最接近点对

题目链接:题目链接

这个博客讲的好，下面将其代码进行了一些优化。
题解

代码

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
#define x first
#define y second
const int N = 1e4 + 10;

typedef pair<double,double>PDD;

PDD p[N],t[N];
int n ;

double distance(PDD a , PDD b){
    double x = a.x - b.x , y = a.y - b.y;
    return sqrt(x * x + y * y);
}

double merge(int left , int right){
    double dis = 1e18; // 左，右两边点对之间的最小值
    if(left == right)return dis;
    // 只有两个点，返回就两个点之间的距离就可以了
    if(left + 1 == right)return distance(p[left] , p[right]);
    int mid = (left + right) >> 1;
    dis = min(dis , merge(left , mid));
    dis = min(dis , merge(mid + 1 ,right));
    int k = 0;
    // 将 这个区间 T 中距离小于 dis 的点加入
    // 这些点有可能是比 dis 小的点
    for(int i = left ; i <= right ; ++i)
        if(fabs(p[i].x - p[mid].x) <= dis)
            t[k++] = p[i];
    // 枚举选出集合点之间的距离，第层循环由性质会减少很多，
    // 不会超过6 个
    for(int i = 0 ; i < k - 1 ; ++i)
        for(int j = i + 1 ; j < k  && t[j].y - t[i].y < dis; ++j)
            dis = min(dis , distance(t[i],t[j]));
    return dis;
}

int main(){
    cin>>n;
    for(int i = 0 ; i < n ; ++i)cin>>p[i].x>>p[i].y;
    sort(p , p + n);
    printf("%.4lf\n",merge(0 , n - 1));
    return 0;
}

棋盘覆盖(地毯填补问题)

相关题目链接：地毯填补问题

解题思路
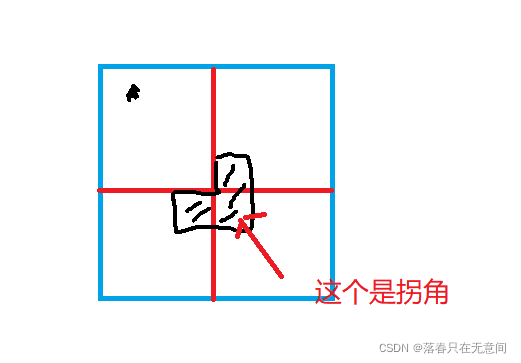
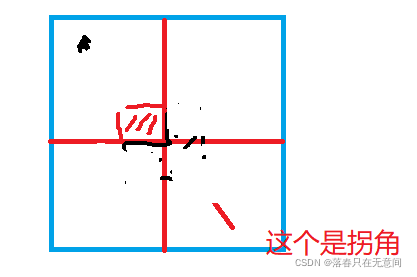
相信来看这篇博客的都知道这个题目为什么能用分治法做吧，因此就不说明了。首先理解题意，题目所说的拐角是什么意思？如图
在这里插入图片描述
那么我们什么依据思路来解决这个问题呢？回顾课本中所说的解法，是分为四个部分后，对着四个部分进行分情况讨论。我们就以左上角为例，如果特殊方格出现在这里，由上面拐角的定义，这个时候我们就要输出如图拐角的坐标，同时这里题目给我们L型方块的标号很有意思，左上角是 1 ，右上角是2 ，左下角是3 ，右下角是4 。之后递归处理，那么如果不在什么办呢？那么我们就会有一个L型方块来使得这个区域存在特除方格，但是我们不用确定方块用了哪一个，但是我们知道，一定有一个特殊方格存在如图所在位置，因此我们递归的参数也要改变

在这里插入图片描述

为什么是这样判断特殊方格在那一个部分的？
首先我们明确我们的图是一个一个点构成的不会有一个明显的中点，如一个4 * 4 的矩阵就会是
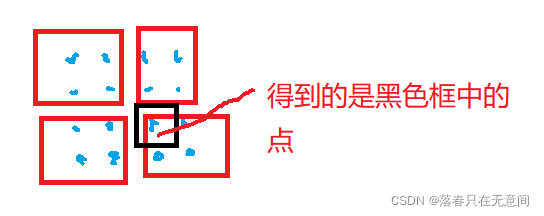
在这里插入图片描述
相信画到这里聪明的你一定能知道了吧

参数意义：

tr:棋盘左上角方格的行号;
dc:特殊方格所在的列号;
tc:棋盘左上角方格的列号;
s: $s=2^k$ ，棋盘规格为 $2^k×2^k$ ;
dr:特殊方格所在的行号。

代码：

#include<iostream>
#include<cmath>
#include<cstring>
using namespace std;
int k;
int  dr,dc;

void show(int x ,int y , int k){
    printf("%d %d %d\n",x  ,y  , k);
}

void dfs(int tr , int tc , int dr ,int dc ,int s){
    if(s == 1)return ;
    s >>= 1;
    int mr = tr + s , mc = tc + s;
    // 左上角
    if(dc < mc && dr < mr)
      {
          show(mr ,mc  ,1 );
          //printf("%d %d 1\n",tr + s - 1 , tc + s - 1);
          dfs(tr , tc , dr,dc , s);
      }
    else
        dfs(tr,tc, mr - 1, mc - 1, s);
    // 右上角
    if(dr < mr && dc >= mc )
    {
        show(mr  ,mc - 1  ,2);
        // printf("%d %d 2\n",tr + s - 1 , tc + s );
        dfs(tr , tc + s , dr,dc , s);
    }
    else
        dfs(tr , tc + s , mr - 1 , mc ,s);
    // 左下角
    if(dr >= mr && dc < mc)
     {
         show(mr - 1  ,mc  ,3 );
         //printf("%d %d 3\n",tr + s , tc + s - 1);
         dfs(tr + s , tc , dr , dc , s);
     }
    else
        dfs(tr + s , tc , mr ,mc - 1 , s);
    
    // 右下角
    if(dr >= mr &&dc >= mc)
     {
         show(mr - 1  ,mc - 1  ,4 );
        // printf("%d %d 4\n",mr , mc );
         dfs(mr , mc , dr , dc , s);
     }
    else
        dfs(tr + s , tc + s ,mr ,mc ,s);
}

int main(){
    cin>>k>>dr>>dc;
    dfs(1 , 1 ,dr,dc,1 << k );
    return 0;
}