[数据结构与算法] 一文带你了解Map和Set、二叉搜索树

方法	解释
V get(Object key)	返回 key 对应的 value
V getOrDefault(Object key, V defaultValue)	返回 key 对应的 value，key 不存在，返回默认值
V put(K key, V value)	设置 key 对应的 value
V remove(Object key)	删除 key 对应的映射关系
Set<K> keySet()	返回所有 key 的不重复集合
Collection<V> values()	返回所有 value 的可重复集合
Set<Map.Entry<K, V>> entrySet()	返回所有的 key-value 映射关系
boolean containsKey(Object key)	判断是否包含 key
boolean containsValue(Object value)	判断是否包含 value

注：

Map是一个接口，不能直接实例化对象。只能实例化TreeMap或HashMap。
Map中存放的Key是唯一的，value是可以重复的（如果重复，存放最新的val值）
HashMap可以存放null，TreeMap不可以。
Map中的Key可以全部分离出来，存储在Set中访问
Map中的value可以全部分离出来，存储在Collection的任何一个子集合中

（2）Map.Entry<K,V>

Map.Entry<K, V> 是Map内部实现的用来存放<key, value>键值对映射关系的内部类，该内部类中主要提供了<key, value>的获取，value的设置以及Key的比较方式。

方法	解释
K getKey()	返回 entry 中的 key
V getValue()	返回 entry 中的 value
V setValue(V value)	将键值对中的value替换为指定value

注：Map.Entry<K,V>并没有提供设置Key的方法

（3）模拟实现HashMap【OJ链接】

底层使用单向链表来实现HashMap

class Node{
    public int key;
    public int value;
    public Node next;
    public Node(int key,int value){
        this.key=key;
        this.value=value;
    }
}
class MyHashMap {
    public Node root;
    public MyHashMap() {
        
    }
    
    public void put(int key, int value) {
        if(root==null){
            root=new Node(key,value);
            return;
        }
        Node cur=root;
        Node prev=null;
        while(cur!=null){
            if(cur.key==key){
                cur.value=value;
                return;
            }
            prev=cur;
            cur=cur.next;
        } 
        prev.next=new Node(key,value);   
    }
    
    public int get(int key) {
        Node cur=root;
        while(cur!=null){
            if(cur.key==key){
                return cur.value;
            }
            cur=cur.next;
        }
        return -1;
    }
    
    public void remove(int key) {
        if(root==null){
            return;
        }
        if(root.key==key){
            root=root.next;
            return;
        }
        Node cur=root.next;
        Node prev=root;
        while(cur!=null){
            while(cur.key==key){
                prev.next=cur.next;
                return;
            }
            prev=cur;
            cur=cur.next;
        }
    }
}

3、Set

Set和Map主要有两点不同：Set是继承自Collection的接口类，Set中只存储了key值。

（1）Set的常用方法

方法	解释
boolean add(E e)	添加元素，但重复元素不会被添加成功
void clear()	清空集合
boolean contains(Object o)	判断 o 是否在集合中
Iterator<E> iterator()	返回迭代器
boolean remove(Object o)	删除集合中的 o
int size()	返回set中元素的个数
boolean isEmpty()	检测set是否为空，空返回true，否则返回false
Object[] toArray()	将set中的元素转换为数组返回
boolean containsAll(Collection<?> c)	集合c中的元素是否在set中全部存在，是返回true，否则返回 false
boolean addAll(Collection<? extends E> c)	将集合c中的元素添加到set中，可以达到去重的效果

注：

Set中只存储了key值，要求key值唯一
Set最大的功能是给集合中元素去重
Set中不能插入为null的key
Set中的key值不能修改
Set的底层是用Map来实现的，使用key和Object的一个默认对象作为键值对插入到Map中

（2）模拟实现HashSet【OJ链接】

使用双向链表来模拟实现HashSet，注意Set是对集合进行去重，所以在添加元素时，如果集合中已经存在，则不需要添加。

class Node{
    public int key;
    public Node next;
    public Node(int key){
        this.key=key;
    }
}
class MyHashSet {
    public Node front;
    public Node rear;
    public MyHashSet() {
    }
    
    public void add(int key) {
        if(front==null){
            front=new Node(key);
            rear=front;
            return;
        }
        Node cur=front;
        //添加之前需要先去重，如果Set中存在这个值，则不需要插入
        while(cur!=null){
            if(cur.key==key){
                return;
            }
            cur=cur.next;
        }
        rear.next=new Node(key);
        rear=rear.next;
    }
    
    public void remove(int key) {
        Node cur=front;
        Node prev=null;
        while(cur!=null){
            if(cur.key==key){
                if(cur==front){
                    front=front.next;
                }else if(cur==rear){
                    prev.next=null;
                    rear=prev;
                }else{
                    prev.next=cur.next;
                }
                return;
            }
            prev=cur;
            cur=cur.next;
        }
    }
    
    public boolean contains(int key) {
        if(front==null){
            return false;
        }
        Node cur=front;
        while(cur!=null){
            if(cur.key==key){
                return true;
            }
            cur=cur.next;
        }
        return false;
    }
}

4、二叉搜索树

二叉搜索树又称二叉排序树：

左子树不为空时，左子树所有节点小于根节点
右子树不为空时，右子树所有节点都大于根节点
左右子树也为二叉搜索树

（1）查找

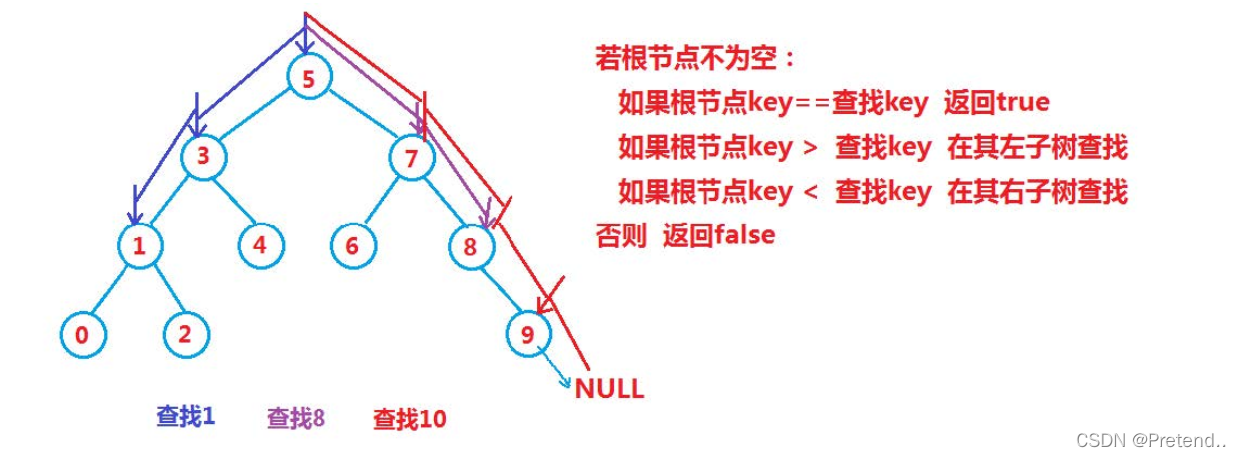
   public boolean search(int val){
        Node1 cur=this.root;
        while(cur!=null){
            if(cur.val==val){
                return true;
            }else if(cur.val>val){
                cur=cur.left;
            }else{
                cur=cur.right;
            }
        }
        return false;
    }

（2）插入

如果树为空，直接插入到根节点

如果树不为空，找到合适的位置插入（插入的节点的父节点左右子树一定都为空）

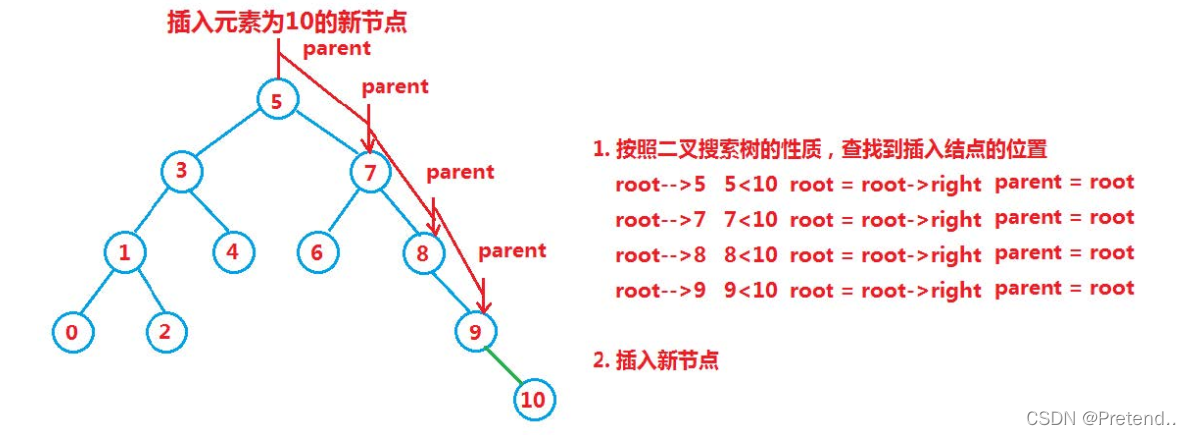
   public boolean insert(int val){
        if(this.root==null){
            root=new Node1(val);
            return true;
        }
        Node1 cur=this.root;
        Node1 parent=null;
        while(cur!=null){
            if(cur.val==val){
                return false;
            }else if(cur.val>val){
                parent=cur;
                cur=cur.left;
            }else{
                parent=cur;
                cur=cur.right;
            }
        }
        if(parent.val>val){
            parent.left=new Node1(val);
        }else{
            parent.right=new Node1(val);
        }
        return true;
    }

（3）删除（重点）

设待删除结点为 cur, 待删除结点的双亲结点为 parent。
1. cur.left == null

1. cur 是 root，则 root = cur.right
2. cur 不是 root，cur 是 parent.left，则 parent.left = cur.right
3. cur 不是 root，cur 是 parent.right，则 parent.right = cur.right

2. cur.right == null

?cur 是 root，则 root = cur.left
?cur 不是 root，cur 是 parent.left，则 parent.left = cur.left
?cur 不是 root，cur 是 parent.right，则 parent.right = cur.left

3. cur.left != null && cur.right != null
? ? ?左右子树都不为空时，使用替换法删除，找到右子树中最小的节点（target），用它的值填补待删除的节点的值，最后只需要删除节点target即可。

   //二叉树的删除
    public boolean remove(int val){
        if(this.root==null){
            return false;
        }
        Node1 cur=this.root;
        Node1 parent=null;
        while(cur!=null){
            if(cur.val==val){
                removeChild(parent,cur);
                return true;
            }else if(cur.val>val){
                parent=cur;
                cur=cur.left;
            }else{
                parent=cur;
                cur=cur.right;
            }
        }
        return false;
    }
    //删除
    public void removeChild(Node1 parent,Node1 cur){
        if(cur.left==null){
            if(cur==root){
                root=root.right;
            }else if(cur==parent.left){
                parent.left=cur.right;
            }else if(cur==parent.right){
                parent.right=cur.right;
            }
        }else if(cur.right==null){
            if(cur==root){
                root=root.left;
            }else if(cur==parent.left){
                parent.left=cur.left;
            }else if(cur==parent.right){
                parent.right=cur.left;
            }
        }else if(cur.left!=null&&cur.right!=null){
            Node1 target=cur.right;
            Node1 targetParent=null;
            while(target.left!=null){
                targetParent=target;
                target=target.left;
            }
            cur.val=target.val;
            if(target==cur.right){
                cur.right=target.right;
            }else{
                targetParent.left=target.right;
            }
        }
    }