归并排序算法思路
从小到大排序时
归并排序算法原理:
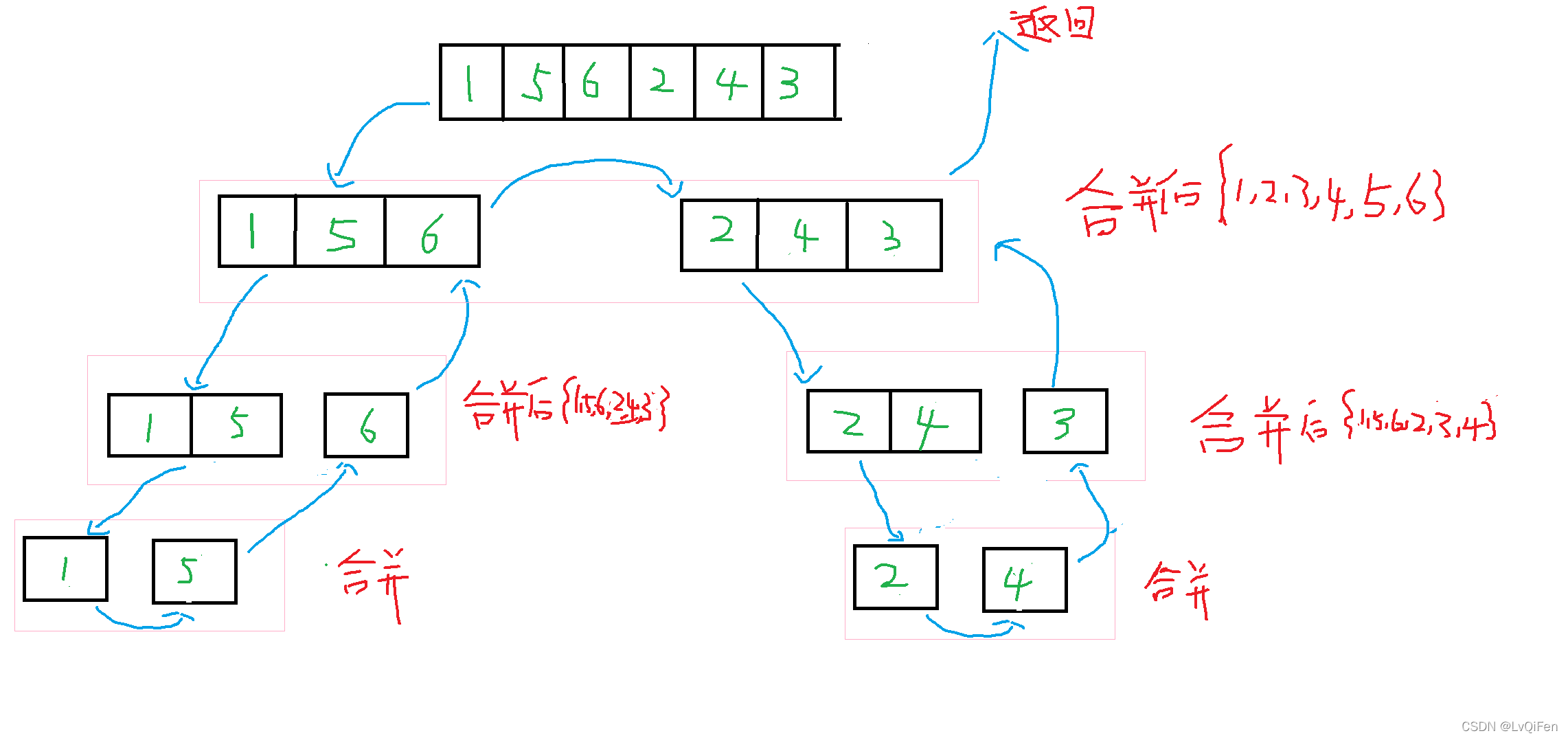
归并排序利用了分治的思想,采用递归来实现
如果要排序一个数组,先把数组从中间分成前后2部分,然后,对前后两部分分别排序
再将排好序的两部分合并在一起,这样整个数组就有序了。递推公式:
1. mergeSort(p,r) = merge(mergeSortCore(p,q),mergeSortCore(q+1,r));
2. q = (p+r)/2;
3. 终止条件:p>=r 不用继续分解
4. p: 每段的起始下标
5. r: 每段的末尾下标
6. q: 每段的中间下标
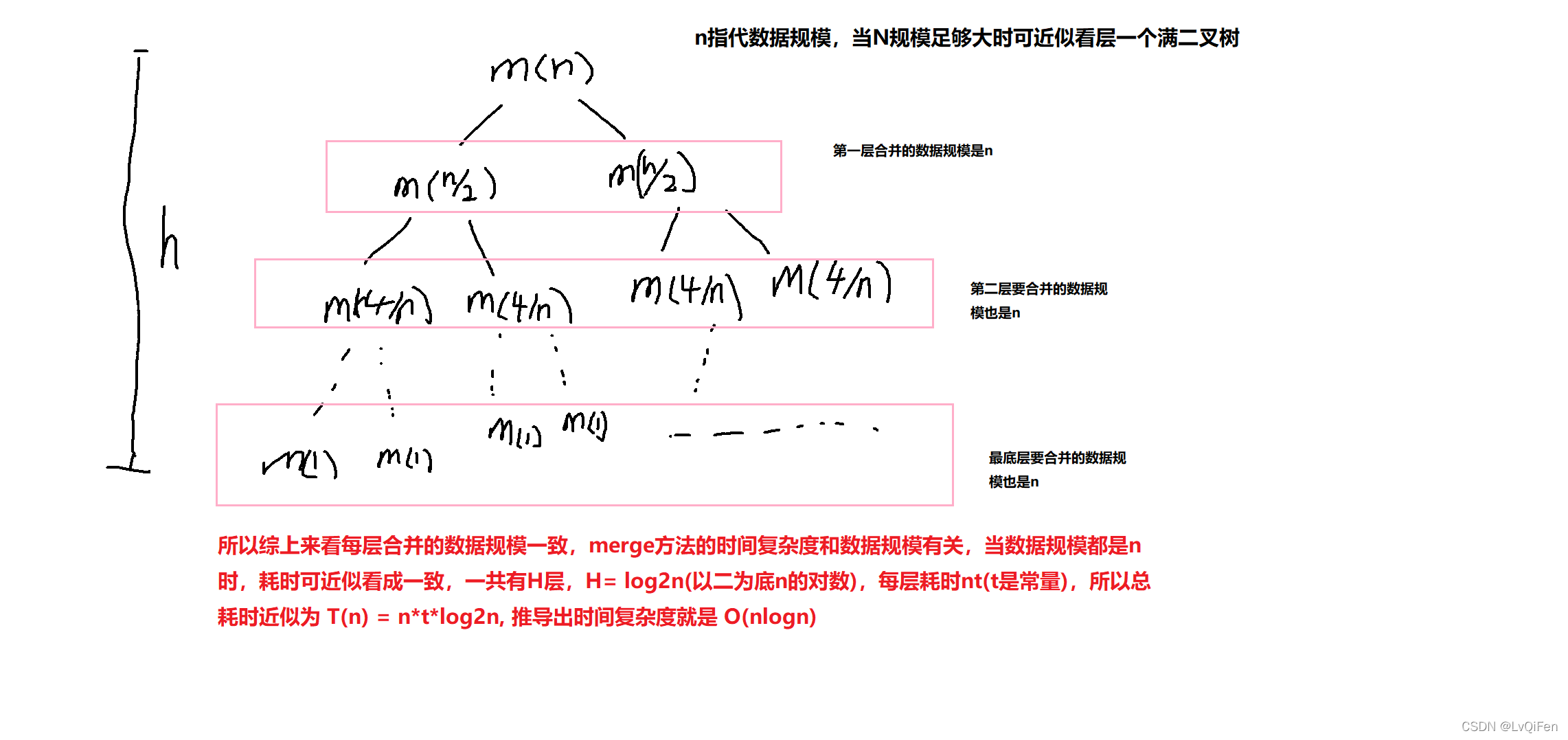
时间复杂度:O(N*logN)
- 归并排序算法的拆分并步耗时是常量级别,耗时是在合并这里,通过上图可以看出是个完全二叉树,当n规模足够大时就可以近似看成是满二叉树,由merge方法来看合并的数据规模足够大时时间复杂度是O(n)
空间复杂度:O(n),归并排序有申请额外的临时数组,并且也有函数调用栈的深度最深也就是树的高度可表示(logN )。由于是在合并的时候才申请的,用完就释放了,所以取最长的那次申请空间是n,比 log ? 2 n \log_2 n log2?n 大 取最大的就是 n。
这里说下该算法函数调用栈的深度H的得来:从图可以看出是一个完全二叉树,设一棵完全二叉树节点个数为N,高度为h。所以总节点个数N满足以下不等式
1 + 2 1 2^1 21 + 2 2 2^2 22+……+ 2 h ? 1 2^{h-1} 2h?1 < N <= 1 + 2 1 2^1 21 + 2 2 2^2 22 +……+ 2 h 2^h 2h 即 2 h ? 1 2^h-1 2h?1 < N <= 2 h + 1 2^{h+1} 2h+1 - 1,所以 2 h 2^h 2h < N+1 <= 2 h + 1 2^{h+1} 2h+1,两边同取以2为底的对数得 h < log ? 2 N + 1 \log_2 {N+1} log2?N+1 <= h+1
时间复杂度和空间复杂度是指算法的执行时间和存储空间与数据规模的之间的增长关系,所以 log ? 2 n \log_2 n log2?n, log ? 2 n + 1 \log_2 {n+1} log2?n+1 都是指代对数级logN归并排序是稳定的排序算法。分2部分后,分别对2部分已排好序的内容进行合并,合并时的条件是
arr[i] <= arr[j],先后顺序不会改变所以是稳定的
总结:归并排序算法的时间复杂度可以做到在任何情况下都是O(nlogn),但是有额外申请空间。
一、核心代码
private static int[] mergeSort(int[] arr) {
if (null == arr || arr.length == 0) {
return arr;
}
// 传入起始下标, 和末尾下标
mergeSortCore(arr, 0, arr.length - 1);
return arr;
}
private static void mergeSortCore(int[] arr, int p, int r) {
if (p >= r) return;
int q = p + (r - p) / 2;
mergeSortCore(arr, p, q);
mergeSortCore(arr, q + 1, r);
// 合并
merge(arr, p, q, r);
}
private static void merge(int[] arr, int p, int q, int r) {
int i = p;
int j = q + 1;
int k = 0;
// 开辟一个能容纳左右2部分数据的临时数组,r,p是下标,以长度为10为例:9-0+1=10
int[] temp = new int[r - p + 1];
while (i <= q && j <= r) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= q) {
temp[k++] = arr[i++];
}
while (j <= r) {
temp[k++] = arr[j++];
}
// 将tem数组拷贝回原数组
for (int l = 0; l < temp.length; l++) {
arr[p + l] = temp[l];
}
}
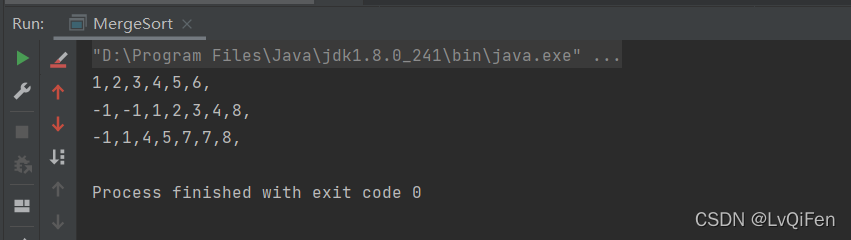
二、测试用例
package arithmetic.ecut.com.排序.a_归并排序;
/**
* 归并排序:
* 归并排序利用了分治的思想,采用递归来实现
* 如果要排序一个数组,先把数组从中间分成前后2部分,然后,对前后两部分分别排序
* 再将排好序的两部分合并在一起,这样整个数组就有序了。
* 递推公式:
* mergeSort(p,r) = merge(mergeSortCore(p,q),mergeSortCore(q+1,r));
* q = (p+r)/2;
* 终止条件:p>=r 不用继续分解
*
* p:每段的起始下标
* r:每段的末尾下标
* q:每段的中间下标
*
* @author 起凤
* @description: TODO
* @date 2022/4/5
*/
public class MergeSort {
public static void main(String[] args) {
// int[] arr = {2, 3, 1, 4, -1, 8, -1};
int[] arr = {1, 5, 6, 2, 4, 3};
int[] sort = mergeSort(arr);
print(sort);
int[] arr1 = {2, 3, 1, 4, -1, 8, -1};
int[] sort1 = mergeSort(arr1);
print(sort1);
int[] arr2 = {-1, 7, 1, 4, 5, 8, 7};
int[] sort2 = mergeSort(arr2);
print(sort2);
}
private static int[] mergeSort(int[] arr) {
if (null == arr || arr.length == 0) {
return arr;
}
// 传入起始下标, 和末尾下标
mergeSortCore(arr, 0, arr.length - 1);
return arr;
}
private static void mergeSortCore(int[] arr, int p, int r) {
if (p >= r) return;
int q = p + (r - p) / 2;
mergeSortCore(arr, p, q);
mergeSortCore(arr, q + 1, r);
// 合并
merge(arr, p, q, r);
}
/**
* 合并
*
* @param arr
* @param p
* @param q
* @param r
*/
private static void merge(int[] arr, int p, int q, int r) {
int i = p;
int j = q + 1;
int k = 0;
// 开辟一个能容纳左右2部分数据的临时数组,r,p是下标,以长度为10为例:9-0+1=10
int[] temp = new int[r - p + 1];
while (i <= q && j <= r) {
if (arr[i] <= arr[j]) {
temp[k++] = arr[i++];
} else {
temp[k++] = arr[j++];
}
}
while (i <= q) {
temp[k++] = arr[i++];
}
while (j <= r) {
temp[k++] = arr[j++];
}
// 将tem数组拷贝回原数组
for (int l = 0; l < temp.length; l++) {
arr[p + l] = temp[l];
}
}
private static void print(int[] sort) {
StringBuilder builder = new StringBuilder();
for (int i = 0; i < sort.length; i++) {
builder.append(sort[i]).append(",");
}
System.out.println(builder);
}
}