0、前言

本篇博客是针对力扣上50题的题解，记载了做题过程中的几种做法，有可实现的，也有不可实现的！具体的题目描述可点击此处进行查看！具体的代码实现以及其他内容可点击此处进行查看！

1、题目描述

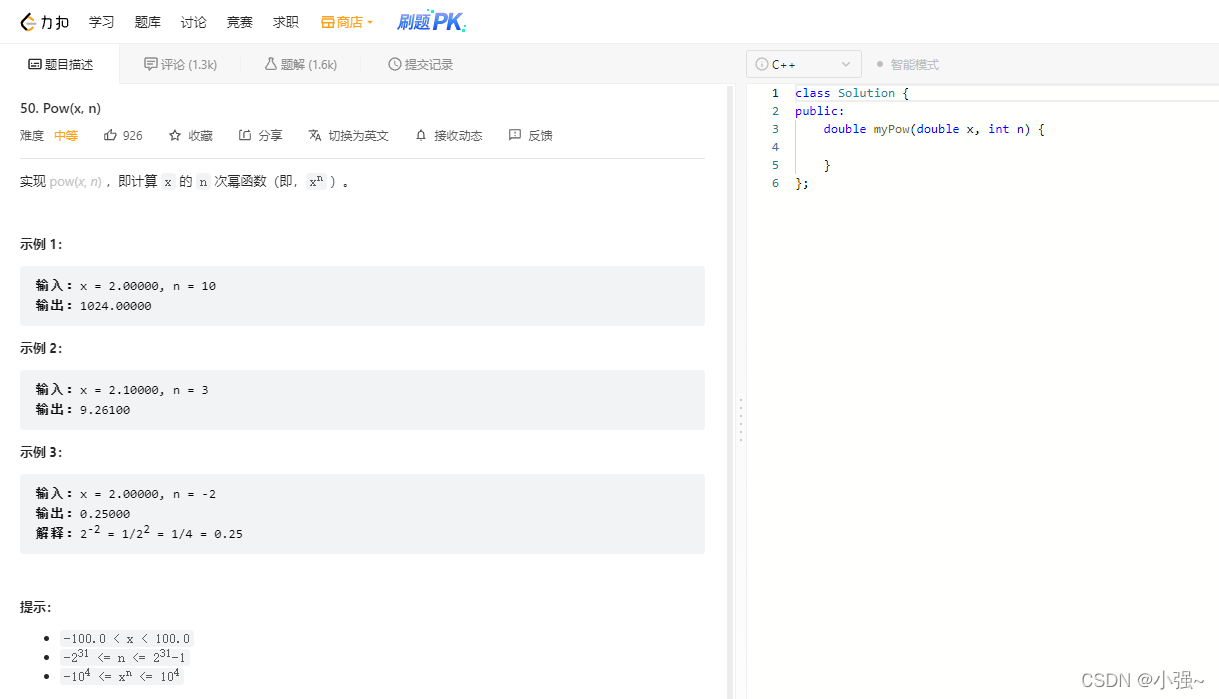
在这里插入图片描述

2、解题思路

2.1 方法1 ~ 利用递归

2.1.1 思路

这种思路就是直接利用递归实现计算 x 的 n 次幂函数，但没考虑当幂次特别大时，程序的运行效率，所以在力扣上有些案例就没通过！在这里就是记录一下自己的弱鸡时间~

2.1.2 程序代码

#include<iostream>
#include<vector>
using namespace std;
#include<algorithm>

/* 方法1 ~ 利用递归 （有问题）*/
double ans(double x, int n)
{
	if (n < 0)
	{
		n = -n;
		x = 1 / x;
	}
	if (n < 1)
		return 1;
	--n;
	return ans(x, n)*x;
}
double myPow(double x, int n)
{
	return ans(x, n);
}

void test()
{
	double x = 2.0; int n = 3;
	cout << "\n输入：x = " << x << "  n = " << n << endl;
	cout << "\n结果：";
	cout << myPow(x,n) << endl << endl;
}

int main()
{
	test();
	system("pause");
	return 0;
}

2.1.3 运行结果

在这里插入图片描述

2.2 方法2 ~ 利用遍历

2.2.1 思路

这又是一个菜鸡想法，依然是运行效率慢，力扣案例也有过不了的，害~

2.2.2 程序代码

#include<iostream>
#include<vector>
using namespace std;
#include<algorithm>

/* 方法2 ~ 遍历 （有问题）*/
double myPow(double x, int n) {
	double res = 1.0;
	if (n < 0) n = -n, x = 1 / x;
	for (int i = 0; i < n; i++)
	{
		res *= x;
	}
	return res;

}

void test()
{
	double x = 2.0; int n = 3;
	cout << "\n输入：x = " << x << "  n = " << n << endl;
	cout << "\n结果：";
	cout << myPow(x,n) << endl << endl;
}

int main()
{
	test();
	system("pause");
	return 0;
}

2.2.3 运行结果

在这里插入图片描述

2.3 方法3 ~ 利用快速幂

2.3.1 思路

这种思路就是利用x的平方取进行操作，例如
举个例子，计算 x^32 可以按照：

x -> x ^2 -> x^4 -> x^8 -> x^16 -> x^32 进行操作，即可以将偶数次的直接乘以x的平方，然后奇数次的乘1（n为偶数）或x（n为奇数）！

2.3.2 程序代码

#include<iostream>
#include<vector>
using namespace std;
#include<algorithm>

/* 方法3 ~ 奇数幂 */
double myPow(double x, int n) {
	double ans = 1.0;
	for (int i = n; i != 0; i /= 2)
	{
		if (i % 2 != 0)
		{
			ans *= x;
		}
		x *= x;
	}
	return n < 0 ? 1 / ans : ans;
}

void test()
{
	double x = 2.0; int n = 3;
	cout << "\n输入：x = " << x << "  n = " << n << endl;
	cout << "\n结果：";
	cout << myPow(x,n) << endl << endl;
}

int main()
{
	test();
	system("pause");
	return 0;
}