1、统计方形
题意概括:给定一个n行,m列的地图,统计其中的正方形个数和长方形个数
解题思路:把这个格子看做是由a[n],b[m]生成,c[i][j] = a[i]*b[j],a和b的每个值都是1
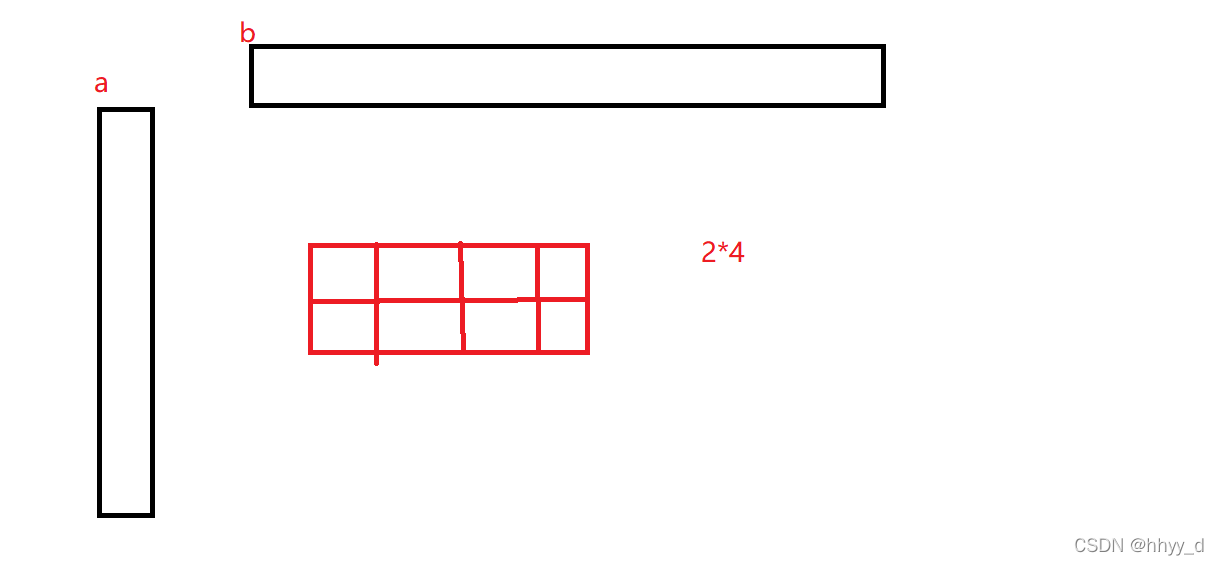
每个图形的生成都由a中连续的1和b中连续的1构成,因此求出不同长宽的矩形即可。利用差分可以预先处理好连续1的个数。
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 5010;
int a[N],b[N];
int n,m;
void insert(int i,int j,int w[])
{
w[i]+=1;
w[j+1]-=1;
}
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin>>n>>m;
for (int i = 1; i <= n; i ++ ) insert(1,i,a);
for (int i = 1; i <= m; i ++ ) insert(1,i,b);
for (int i = 1; i <= n; i ++ ) a[i]+=a[i-1];
for (int i = 1; i <= m; i ++ ) b[i]+=b[i-1];
long long ans1 = 0, ans2 = 0;
int len1 = min(n,m),len2 = max(n,m);
for (int i = 1; i <= n; i ++ )
{
for (int j = 1; j <= m; j ++ )
{
if(i == j ) ans1+=(a[i]*b[j]);
else ans2+=(a[i]*b[j]);
}
}
cout<<ans1<<" "<<ans2<<endl;
return 0;
}
2、子矩阵计数
题意概括:一个数组a,一个数组b,值为0或者1,c[i][j] = a[i]*b[j],给定k,求c中面积大小为k的矩形有多少个
解题思路:按照上一个的想法,对k进行枚举即可。
代码如下:
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 4e4+10;
int a[N],b[N];
int s1[N],s2[N];
int n,m,k;
void deal(int w[],int s[],int len)
{
int sum = 0;
for(int i=1;i<=len;i++)
{
if(w[i])
{
sum++;
s[1]+=1;
s[sum+1]-=1;
}
else sum = 0;
}
for(int i=1;i<=len;i++) s[i]+=s[i-1];
}
int main()
{
cin>>n>>m>>k;
for (int i = 1; i <= n; i ++ ) cin>>a[i];
for (int i = 1; i <= m; i ++ ) cin>>b[i];
deal(a,s1,n);
deal(b,s2,m);
long long ans = 0;
for(int i=1;i<=n;i++)
{
if(k%i!=0) continue;
int j = k/i;
if(j > m) continue;
ans+=s1[i]*s2[j];
}
cout<<ans<<endl;
return 0;
}
3、最大子矩阵
题意概括:
解题思路:还是把生成的矩形看作是两个数组的乘积,要满足要求,同等长度下肯定选择乘积最小的,因此s[i]表示数组长度i时的最小值,枚举s1数组的每个长度,求满足条件的s2数组的位置,然后取最大即可
#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long LL;
const int N = 2010,inf = 0x3f3f3f3f;
int a[N],b[N];
int s1[N],s2[N];
int n,m;
LL k;
void work(int w[],int s[],int n)
{
for(int len=1;len<=n;len++)
{
s[len] = inf;
for(int r = len;r<=n;r++)
{
s[len] = min(s[len],w[r] - w[r-len]);
}
}
}
int main()
{
cin>>n>>m;
int x;
for (int i = 1; i <= n; i ++ )
{
cin>>x;
a[i] = a[i-1]+x;
}
for (int i = 1; i <= m; i ++ )
{
cin>>x;
b[i] = b[i-1]+x;
}
cin>>k;
work(a,s1,n);
work(b,s2,m);
int ans = 0;
for(int i=1;i<=n;i++)
{
int l = 0,r = m;
while(l < r)
{
int mid = (l+r+1) >> 1;
if((LL)s1[i]*s2[mid] <= k) l = mid;
else r = mid-1;
}
ans = max(ans,i*l);
}
cout<<ans<<endl;
return 0;
}
