1. 线索二叉树

1.1 基本概念

遍历二叉树是以一定规则将二叉树中的节点排列成一个线性序列。该序列中每个节点（第一个和最后一个除外）都有一个直接的前驱和直接后继。

传统二叉链表存储仅能体现一种父子关系，不能直接得到节点在遍历中的前驱和后继。
在含有n个节点的二叉树中，共有n+1个空链域。

（1）定义
规定：

若无左子树，令lchild指向其前驱节点。
若无右子树，令rchild指向其后继节点。
增加两个标志ltag, rtag表示左右孩子指针是否指向前驱或后继节点。

1.2 线索二叉树的构造

二叉树的线索化就是将空指针改为指向前驱或后继的线索。
因为前驱和后继信息只有在遍历时才能获得，因此线索二叉树的构造本质上是二叉树的遍历。
假设：

指针pre指向刚刚访问过的节点，即前驱节点。
指针p指向正在访问的节点。

易错点

最后一个节点的后继节点需要单独判断并选择。
先序遍历时，若节点的左孩子已经线索化，则不需要再对其左孩子进行线索化。

因为只有先序遍历在对节点线索化后，还可能对其左子树进行访问。我们不需要再次访问节点的前驱节点。

1.2.1 中序线索二叉树的构造

在这里插入图片描述

中序遍历： B D A E C
思想：
①本质上是中序遍历算法，但需要保存pre值。
②访问节点q时，需要判断节点左孩子指针是否为空。
③若左孩子指针为空，则可以赋予前驱线索pre。同时若pre的右孩子指针为空，可以同时赋予pre的后继线索。
④最后一个节点的右孩子指针若为空，则需要将其设置为NULL后继线索。

void InTread(TreadTree &p, TreadTree &pre){
	if(p !=NULL){
		InTread(p->lchild, pre);
		// 判断左孩子指针是否为空
		if(p->lchild == NULL){
		// pre为当前节点的前驱节点
			p->lchild = pre;
			p->ltag = 1;
		}
		// 判断前驱节点是否为空，其右孩子指针是否为空。
		if(pre != NULL && pre->rchild == NULL){
		// p为pre的后继节点
			pre->rchild = p;
			pre->rtag  = 1;
		}
		
		pre = p;
		
		InTread(p->rchild, pre);
	}
}

/*中序线索二叉树构造*/
void CreateInTread(TreadTree T){
	TreadTree pre = NULL;
	if(T != NULL){
		InTread(T, pre);
		if(pre->rchild ==NULL)
			pre->rtag = 1;
	}
}

为什么不能直接通过中序遍历序列获得节点的前驱和后继节点，而需要再次遍历一遍呢？
理解：我们确实可以通过中序遍历序列直接获解。但是我们只需要赋予节点的空指针线索值，对于非空孩子指针不需要变化。

1.2.2 先序线索二叉树的构造

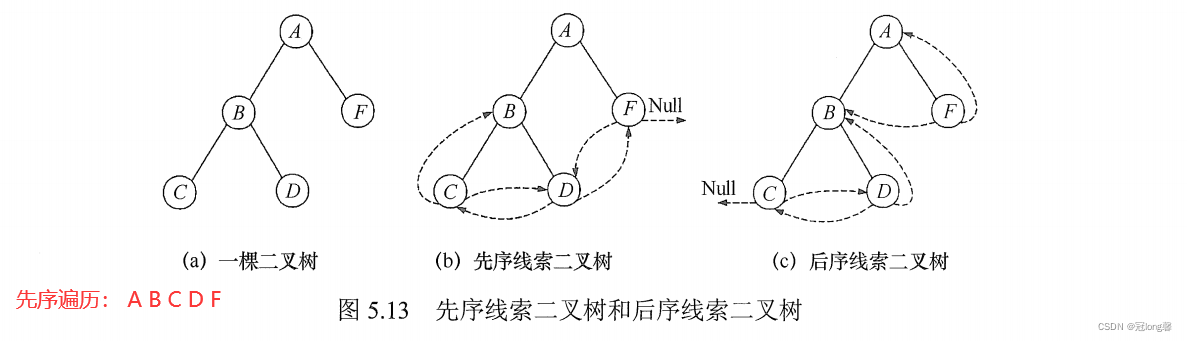
在这里插入图片描述

先序遍历： A B D D F
思想：
①本质上是先序遍历算法，但需要保存pre值。
②访问节点q时，需要判断节点左孩子指针是否为空。
③若左孩子指针为空，且则可以赋予前驱线索pre。同时若pre的右孩子指针为空，可以同时赋予pre的后继线索。
④最后一个节点的右孩子指针若为空，则需要将其设置为NULL后继线索。
⑤当节点左孩子没有进行线索化时，可以对其左子树进行线索化构造。因为此时左子树并不指向前驱节点。

void PreTread(TreadTree p, TreadTree &pre){
	if(p != NULL){
		/*线索化*/
		if(p->lchild == NULL){
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre != NULL && pre->rchild == NULL){
			pre->rchild = p;
			pre->rtag = 1;
		}
		// 防止循环访问
		if(p->ltag == 0)
			PreTread(p->lchild, pre);
		PreTread(p->rchild, pre);
	}
}

/*先序线索二叉树构造*/
void CreatePreTread(TreadTree T){
	TreadTree pre = NULL;
	if(T != NULL){
		PreTread(T, pre);
		if(pre->rchild == NULL)
			pre->rtag = 1;
	}
}

为什么节点左孩子线索化后不应该在访问其左子树？
理解： 左孩子线索化后，左孩子指针指向其前驱节点。因为我们是按照遍历序列进行线索化的，对于已经访问过的节点不应该在进行线索化。

1.2.3 后序线索二叉树的构造

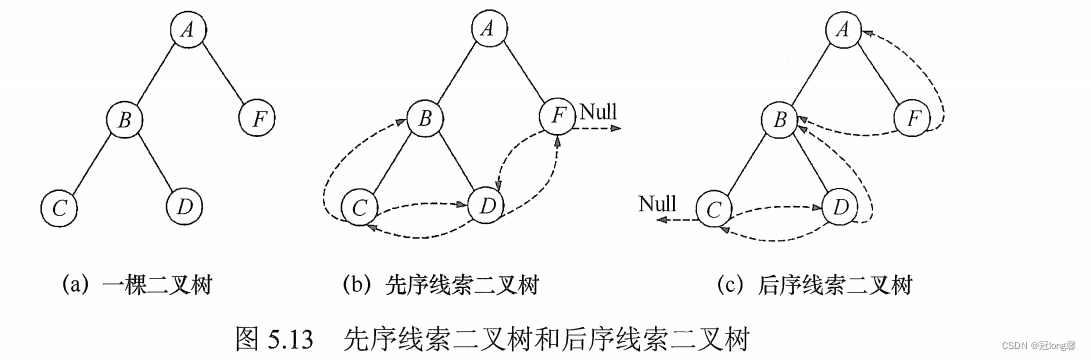
在这里插入图片描述

后序遍历： C D B F A
思想
①本质上是后序遍历算法，但需要保存pre值。
②访问节点q时，需要判断节点左孩子指针是否为空。
③若左孩子指针为空，且则可以赋予前驱线索pre。同时若pre的右孩子指针为空，可以同时赋予pre的后继线索。
④最后一个节点的右孩子指针若为空，则需要将其设置为NULL后继线索。

void PostTread(TreadTree p, TreadTree &pre){
	if(p != NULL){
		PostTread(p->lchild, pre);
		PostTread(p->rchild, pre);
		/*线索化*/
		if(p->lchild == NULL){
			p->lchild = pre;
			p->ltag = 1;
		}
		if(pre != NULL && pre->rchild != NULL){
			pre->rchild = p;
			pre->rtag = 1;
		}
	}
}

/*构造后序线索二叉树*/
void createPostTread(TreadTree T){
	TreadTree pre = NULL;
	if(T != NULL){
		PostTread(T, pre);
		if(T->rchild == NULL)
			T->rtag = 1;
	}
}

1.3 线索二叉树的遍历

1.3.1 中序线索二叉树的后继遍历

（1）思想
当前节点的后继节点有两种寻找方法：

若节点的 $r t a g = 1$ ，表示右孩子指针已经线索化，指向其后继节点，则后继节点为 $r c h i l d$ 。
若节点的 $r t a g = 0$ ，则后继节点应该为其右子树中最左下的节点。

/*寻找子树中，第一个被遍历的节点*/
TreadNode *Firstnode(TreadNode *p){
	while(p->lchild != NULL)
		p = p->lchild
	// 找到最左下节点
	return p;
}

/*寻找后继节点*/
TreeNode *Nextnode(TreadNode *p){
	// 若右孩子指针非线索，则返回最左下节点
	if(p->rtag ==0)
		return Firstnode(p);
	return p->rchild;
}

/*中序遍历*/
void InOrder(TreadNode *T){
	for(TreadNode *p =Firstnode(T); p !=NULL; p =Nextnode(p))
		visit(p);
}